(人教版)2022-2023学年七年级数学下册9.1 不等式 同步测试
试卷更新日期:2023-03-14 类型:同步测试
一、单选题
-
1. 如图所示,在数轴上表示了某不等式的解集,则这个不等式可能是( )
 A、x≤1 B、x≤-1 C、x≥1 D、x≥-12. 下列式子:①-2≤0;②3x+2y>0;③b=2;④m≠3;⑤x+y;⑥x+5≤6是不等式的有( )A、3个 B、4个 C、5个 D、6个3. 下列实数中,不是的解的是( )A、-3 B、-1 C、0 D、3.54. 不等式的解集在数轴上的表示,正确的是( )A、
A、x≤1 B、x≤-1 C、x≥1 D、x≥-12. 下列式子:①-2≤0;②3x+2y>0;③b=2;④m≠3;⑤x+y;⑥x+5≤6是不等式的有( )A、3个 B、4个 C、5个 D、6个3. 下列实数中,不是的解的是( )A、-3 B、-1 C、0 D、3.54. 不等式的解集在数轴上的表示,正确的是( )A、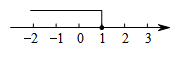 B、
B、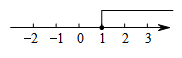 C、
C、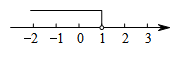 D、
D、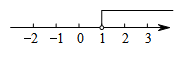 5. 不等式x≤2的解集在数轴上表示正确的是()A、
5. 不等式x≤2的解集在数轴上表示正确的是()A、 B、
B、 C、
C、 D、
D、 6. 若的结果在两个相邻整数之间,则这两个整数分别是( )A、1和2 B、2和3 C、3和4 D、0和17. 若 , 则下列不等式中错误的是( )A、 B、 C、 D、8. 若 , a为任意实数,则下列结论正确的是( )A、 B、 C、 D、9. 已知a<b,则下列式子正确的是( )A、a+5>b+5 B、3a>3b C、﹣5a>﹣5b D、10. 已知 , 则下列不等式错误的是( )A、 B、 C、 D、
6. 若的结果在两个相邻整数之间,则这两个整数分别是( )A、1和2 B、2和3 C、3和4 D、0和17. 若 , 则下列不等式中错误的是( )A、 B、 C、 D、8. 若 , a为任意实数,则下列结论正确的是( )A、 B、 C、 D、9. 已知a<b,则下列式子正确的是( )A、a+5>b+5 B、3a>3b C、﹣5a>﹣5b D、10. 已知 , 则下列不等式错误的是( )A、 B、 C、 D、二、填空题
-
11. 若m>n,则﹣2m﹣2n(填>,<)12. 已知 , 则 . (填>、=或<)13. 由2m>6得到m>3,则变形的依据是 .14. 已知 , 则(用“>”或“<”号填空).15. 无理数的小数部分是 .
三、解答题
-
16. 求不等式 的所有正整数解.17. 若不等式组 无解,求m的取值范围.18. 现有不等式的两个性质:
①在不等式的两边都加上(或减去)同一个整式,不等号的方向不变;
②在不等式的两边都乘以同一个数(或整式),乘的数(或整式)为正时不等号的方向不变,乘的数(或整式)为负时不等号的方向改变.
请解决以下两个问题:
(1)、利用性质①比较2a与a的大小(a≠0);(2)、利用性质②比较2a与a的大小(a≠0).四、综合题
-
19. 某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车,恰好全部坐满,已知每辆大客车的乘客座位数比小客车多17个.(1)、求每辆大客车和每辆小客车的乘客座位数;(2)、由于最后参加活动的人数增加了30人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,且所有参加活动的师生都有座位,求租用小客车数量的最大值.20. 【阅读】在证明命题“如果 , , 那么”时,小明的证明方法如下:
证明:∵ ,
∴> ▲ . ∴ ▲ .
∵ , ,
∴ ▲ . ∴ ▲ .
∴.
【问题解决】
(1)、请将上面的证明过程填写完整;(2)、有以下几个条件:① , ② , ③ , ④ .请从中选择两个作为已知条件 , 得出结论 .你选择的条件序号是 ,并给出证明过程 .21. 数学课上,老师出了一道题:比较 与 的大小.小华的方法是:
因为 >4,所以 ﹣2_____2,所以 _____ (填“>”或“<”);
小英的方法是:
﹣ = ,因为19>42=16,所以 ﹣4____0,所以 ____0,所以 _____ (填“>”或“<”).
(1)、根据上述材料填空;(2)、请从小华和小英的方法中选择一种比较 与 的大小.