2022-2023学年浙教版数学八年级下册4.2平行四边形 课后测验
试卷更新日期:2023-03-14 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 如图,在平行四边形ABCD中,∠B=60°,则∠D=( )
 A、60° B、120° C、140° D、30°2. 平行四边形的对角线( )A、相等 B、互相垂直 C、互相平分 D、互相垂直且平分3. 若平行四边形ABCD的周长为32,AB=4,则BC的长是( )A、6 B、8 C、12 D、164. 如图,在中,DE平分 , , 则( )
A、60° B、120° C、140° D、30°2. 平行四边形的对角线( )A、相等 B、互相垂直 C、互相平分 D、互相垂直且平分3. 若平行四边形ABCD的周长为32,AB=4,则BC的长是( )A、6 B、8 C、12 D、164. 如图,在中,DE平分 , , 则( )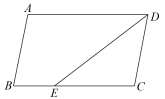 A、30° B、45° C、60° D、80°5. 已知▱的对角线 , 的长分别为 , , 则长的范围是( )A、 B、 C、 D、6. 如图,在 中, 与 相较于 , 为 中点,连接 ,则下列结论不一定成立的是( )
A、30° B、45° C、60° D、80°5. 已知▱的对角线 , 的长分别为 , , 则长的范围是( )A、 B、 C、 D、6. 如图,在 中, 与 相较于 , 为 中点,连接 ,则下列结论不一定成立的是( ) A、 B、 C、 且 D、7. 在同一平面内,设a、b、c是三条互相平行的直线,已知a与b间的距离为 , b与c间的距离为 , 则a与c间的距离为( )cm.A、3 B、7 C、3或7 D、2或38. 如图,在 ▱ ABCD中,对角线AC,BD相交于点O,过点O的直线EF交AB于点E,交CD于点F,且 , 若 , 则阴影部分面积是( )
A、 B、 C、 且 D、7. 在同一平面内,设a、b、c是三条互相平行的直线,已知a与b间的距离为 , b与c间的距离为 , 则a与c间的距离为( )cm.A、3 B、7 C、3或7 D、2或38. 如图,在 ▱ ABCD中,对角线AC,BD相交于点O,过点O的直线EF交AB于点E,交CD于点F,且 , 若 , 则阴影部分面积是( ) A、 B、 C、2 D、39. 如图,在▱ABCD中,以点C为圆心,适当长度为半径作弧,分别交CD、BC于点F、G,再分别以点F、G为圆心,大于长为半径作弧,两弧交于点H,作射线CH交AD于点E,连接BE,若DE=5,AE=3,BE=4,则CE的长为( )
A、 B、 C、2 D、39. 如图,在▱ABCD中,以点C为圆心,适当长度为半径作弧,分别交CD、BC于点F、G,再分别以点F、G为圆心,大于长为半径作弧,两弧交于点H,作射线CH交AD于点E,连接BE,若DE=5,AE=3,BE=4,则CE的长为( ) A、 B、 C、 D、810. 如图,在给定的正方形中,点E从点B出发,沿边方向向终点C运动, 交于点F,以 , 为邻边构造平行四边形 , 连接 , 则的度数的变化情况是( )
A、 B、 C、 D、810. 如图,在给定的正方形中,点E从点B出发,沿边方向向终点C运动, 交于点F,以 , 为邻边构造平行四边形 , 连接 , 则的度数的变化情况是( )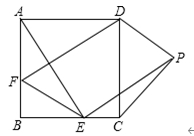 A、一直减小 B、一直减小后增大 C、一直不变 D、先增大后减小
A、一直减小 B、一直减小后增大 C、一直不变 D、先增大后减小二、填空题(每题5分,共30分)
-
11. 已知平行四边形中,比小40°,那么的度数是 .12. 已知中, , 且AB的长是周长的 , 那么 .13. 我们在生活中经常见到如图所示的电动伸缩门,它能伸缩是利用了四边形的 .
 14. 平行四边形中,对角线、交于点O,点E是的中点.若 , 则的长为 .15. 如图,在平行四边形ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB于点F,交DC的延长线于点G,则DE= .
14. 平行四边形中,对角线、交于点O,点E是的中点.若 , 则的长为 .15. 如图,在平行四边形ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB于点F,交DC的延长线于点G,则DE= . 16. 如图①,点为□边上的一个动点,并沿的路径移动到点停止;设点经过的路径长为 , △的面积为 , 与的函数图象如图②所示;若 , 则□的面积是 .
16. 如图①,点为□边上的一个动点,并沿的路径移动到点停止;设点经过的路径长为 , △的面积为 , 与的函数图象如图②所示;若 , 则□的面积是 .
三、作图题(共6分)
-
17. 如图,在6 8的网格图中,A,B,C三点都在格点上,连接AB,试以AB边,画两个以A,B,C为其中三个顶点的平行四边形(要求四个顶点都在格点上).

四、解答题(共8题,共84分)
-
18. 如图所示,a∥b,点A,E,F在直线a上,点B,C,D在直线b上,BC=EF,△ABC与△DEF的面积相等吗?为什么?
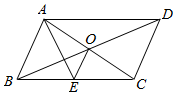
 19. 如图,将▱ABCD的对角线BD向两个方向延长,分别至点E和点F,且使BE=DF.求证:四边形AECF是平行四边形.
19. 如图,将▱ABCD的对角线BD向两个方向延长,分别至点E和点F,且使BE=DF.求证:四边形AECF是平行四边形. 20. 如图,E、F是▱ABCD的对角线AC上的两点,且AE=CF.试判断BE与DF 的数量关系,并说明理由.
20. 如图,E、F是▱ABCD的对角线AC上的两点,且AE=CF.试判断BE与DF 的数量关系,并说明理由. 21. 如图,在中, , 过点A作于点E,连接BE,延长EA至点F,使 , 连接DF.求证: .
21. 如图,在中, , 过点A作于点E,连接BE,延长EA至点F,使 , 连接DF.求证: . 22. 如图,在△ABC中,BC=6cm.射线AG∥BC,点E从点A出发沿射线AG以2cm/s的速度运动,当点E先出发1s后,点F也从点B出发沿射线BC以 cm/s的速度运动,分别连结AF,CE.设点F运动时间为t(s),其中t>0.
22. 如图,在△ABC中,BC=6cm.射线AG∥BC,点E从点A出发沿射线AG以2cm/s的速度运动,当点E先出发1s后,点F也从点B出发沿射线BC以 cm/s的速度运动,分别连结AF,CE.设点F运动时间为t(s),其中t>0. (1)、当t为何值时,∠BAF<∠BAC;(2)、当t为何值时,AE=CF;(3)、当t为何值时,S△ABF+S△ACE<S△ABC .23. 如图,在平面直角坐标系中,的顶点O,B的坐标分别为 , , 将沿对角线翻折得到(点O,A,D在同一直线上),边与边相交于点E,此时,是等边三角形.
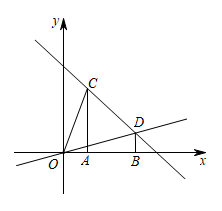
(1)、当t为何值时,∠BAF<∠BAC;(2)、当t为何值时,AE=CF;(3)、当t为何值时,S△ABF+S△ACE<S△ABC .23. 如图,在平面直角坐标系中,的顶点O,B的坐标分别为 , , 将沿对角线翻折得到(点O,A,D在同一直线上),边与边相交于点E,此时,是等边三角形.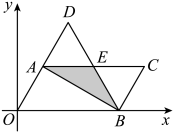 (1)、求线段的长;(2)、求重叠部分的面积;(3)、点N在轴上,点M在直线上,若以点B,C,M,N为顶点的四边形是平行四边形时,请直接写出点M的坐标.
(1)、求线段的长;(2)、求重叠部分的面积;(3)、点N在轴上,点M在直线上,若以点B,C,M,N为顶点的四边形是平行四边形时,请直接写出点M的坐标.
-