2022-2023学年浙教版数学八年级下册4.1四边形 课后测验

试卷更新日期：2023-03-14 类型：同步测试

进入 出卷网 下载

一、单选题（每题3分，共30分）

  • 1. 一个多边形的每一个内角都是135°，则这个多边形是（　　）
    A、七边形 B、八边形 C、九边形 D、十边形

    查看试题解析

  • 2. 永寺双塔，又名凌霄双塔，是我市现存最高的古建筑，均为十三层八角形楼阁式砖塔，如图的正八边形是双塔平面示意图，其每个内角的度数为（  ）

    A、80° B、100° C、120° D、135°

    查看试题解析

  • 3. 若n边形的内角和等于外角和的3倍，则边数n为（  ）
    A、6 B、7 C、8 D、9

    查看试题解析

  • 4. 在四边形ABCD中， ∠A 的对角是（     ）
    A、∠A B、∠B C、∠C D、∠D

    查看试题解析

  • 5. 一个多边形的内角和为α ， 外角和为β ， 则α=2β的多边形的是（  ）
    A、 B、 C、 D、

    查看试题解析

  • 6. 如图，将边长相等的正方形、正五边形和正六边形摆放在平面上，则 ∠1 为 (    )

    A、32° B、36° C、40° D、42°

    查看试题解析

  • 7. 一个多边形从一个顶点可引对角线3条，这个多边形内角和等于（  ）
    A、360° B、540° C、720° D、900°

    查看试题解析

  • 8. 如图，五边形ABCDE是正五边形，F，G是边CD，DE上的点，且BF∥AG．若∠CFB=57°，则∠AGD=（ ）

    A、108° B、36° C、129° D、72°

    查看试题解析

  • 9. 如图，五边形ABCDE中，AB∥CD，∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角，若∠1＝32°，∠3＝60°，则∠2等于（   ）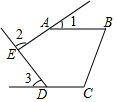

    A、92° B、88° C、98° D、无法确定

    查看试题解析

  • 10. 下列结论：

    ①矩形的对角线相等；

    ②用配方法解一元二次方程x2﹣6x＝8时，此方程可变形为（x﹣3）2＝1；

    ③若一个多边形的内角和等于它的外角和，则这个多边形是四边形；

    ④在直角坐标系中，点P（2，a﹣1）与点Q（b+2，3）关于原点对称，则a+b＝﹣6；

    其中正确结论有（  ）

    A、1个 B、2个 C、3个 D、4个

    查看试题解析

二、填空题（每题5分，共30分）

  • 11. 一个多边形的每一个外角都为36° ， 则这个多边形是边形．

    查看试题解析

  • 12. 足球表面为什么用正六边形和正五边形构成？因为正六边形的两个内角和正五边形的一个内角加起来接近一个周角，而又不足一个周角．这样，由平面折叠而成的多面体充气后最终就呈现为球形．如图，在折叠前的平面上，拼接点处的缝隙∠AOB的大小为  ．

    查看试题解析

  • 13. 在平行四边形ABCD中，∠A：∠B：∠C：∠D=1：3：1：3 ， 则∠A=.

    查看试题解析

  • 14. 如图，平移图形M，与图形N可以拼成一个平行四边形，则图中α的度数是。

    查看试题解析

  • 15. 如图是由射线AB，BC，CD，DE，EF，FA组成的平面图形，则∠1+∠2+∠3+∠4+∠5+∠6=°．

    查看试题解析

  • 16. 如图，在△ABC中，∠BAC为钝角，AF，CE都是这个三角形的高，P为AC的中点．若∠B＝35°，则∠EPF的度数为 ．

    查看试题解析

三、作图题（共12分）

  • 17. 如图是一个多边形，你能否用一直线去截这个多边形，使得到的新多边形分别满足下列条件： ( 画出图形，把截去的部分打上阴影 )

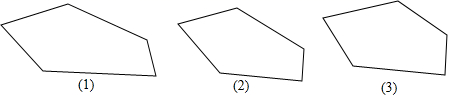    (1)、①新多边形内角和比原多边形的内角和增加了 180∘ ．

    ②新多边形的内角和与原多边形的内角和相等．

    ③新多边形的内角和比原多边形的内角和减少了 180∘ ．

    (2)、将多边形只截去一个角，截后形成的多边形的内角和为 2520∘ ，求原多边形的边数．

    查看试题解析

四、解答题（共7题，共78分）

  • 18. 在四边形ABCD中，∠D=60°，∠B比∠A大20°，C是∠A的2倍，求∠A，∠B，∠C的大小。

    查看试题解析

  • 19. 如图，在四边形ABCD中，∠A=∠B=∠C，点E在边AB上，∠AED=60°

    求证：∠ADE=13∠ADC。

    查看试题解析

  • 20. 如图，求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.

    查看试题解析

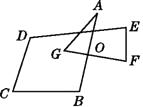  • 21.

    （1）已知：如图1，P为△ADC内一点，DP、CP分别平分DP、CP分别平公∠ADC和∠ACD，如果∠A=60°，那么∠P的度数；如果∠A=90°，那么∠P的度数；如果∠A=x°，则∠P的度数；（答案直接填在题中横线上）

    （2）如图2，P为四边形ABCD内一点，DP、CP分别平分∠ADC和∠BCD，试探究∠P与∠A+∠B的数量关系，并写出你的探索过程；

    （3）如图3，P为五边形ABCDE内一点，DP、CP分别平分DP、CP分别平公∠ADC和∠ACD，请直接写出∠P与∠A+∠B+∠E的数量关系

    （4）如图4，P为六边形ABCDEF内一点，DP、CP分别平分DP、CP分别平公∠ADC和∠ACD，请直接写出∠P与∠A+∠B+∠E+∠F的数量关系

    （5）若P为n边形A1A2A3…An内一点，PA1平分∠AnA1A2 ， PA2平分∠A1A2A3 ， 请直接写出∠P与∠A3+A4+A5+…∠An的数量关系：

    查看试题解析

  • 22. 已知在四边形ABCD中， ∠A=x ， ∠C=y (0°<x<180° ， 0°<y<180°) .

    (1)、∠ABC+∠ADC= (用含 x+y 的代数式直接填空)；
    (2)、如图1，若x=y=90°，DE平分∠ADC，BF平分∠CBM，DE与BC交于点G，

    求证：DE⊥BF；

    (3)、如图2，∠DFB为四边形ABCD的∠ABC，ADC相邻的外角平分线所在直线构成的锐角.若x+y=120°，∠DFB=20°，请直接写出x，y的值.

    查看试题解析

  • 23.

    已知凸四边形ABCD中，∠A=∠C=90°．

    (1)、如图1，若DE平分∠ADC，BF平分∠ABC的邻补角，判断DE与BF位置关系并证明．

    (2)、如图2，若BF、DE分别平分∠ABC、∠ADC的邻补角，判断DE与BF位置关系并证明．

    查看试题解析

  • 24. 如图①，∠1、∠2是四边形ABCD的两个不相邻的外角．

    (1)、猜想并说明∠1+∠2与∠A、∠C的数量关系；
    (2)、如图②，在四边形ABCD中，∠ABC与∠ADC的平分线交于点O．若∠A＝58°，∠C＝152°，求∠BOD的度数；
    (3)、如图③，BO、DO分别是四边形ABCD外角∠CBE、∠CDF的角平分线．请直接写出∠A、∠C与∠O的数量关系．

    查看试题解析