（华师大版）2022-2023学年九年级数学下册28.2 用样本估计总体 同步测试
试卷更新日期：2023-03-13 类型：同步测试
一、单选题
-
1. 一池塘中大约有鱼苗数为50 000尾，为了解池塘中鱼苗的长势，现需从中捞取一些鱼苗进行抽样调查，那么捞出鱼苗数最合适的是（ ）A、1尾 B、50尾 C、500尾 D、1 000尾2. 下列调查方式的选择正确的是（ ）A、为了解青年人的体质状况，选择运动员进行调查 B、为了解全市老年人的健康状况，选择公园中散步的老人进行调查 C、为了解某省所有家庭的用电情况，随机抽查某个小区所有家庭的用电情况 D、为了解10箱某种汽水的质量，随机抽取10瓶进行鉴定3. 在对300名学生考试成绩用简单随机抽样方式进行抽样调查时，第一次从盒子中抽出表示一个编号的纸条，那么，在抽下一个表示编号的纸条之前，他已抽出的这个纸条放入盒子是（ ）A、应当的 B、不应当的 C、没有影响 D、以上都不对4. 下列表述不正确的是（ ）A、样本选取不当时，用样本估计总体不可靠 B、有的较小的样本的平均数和标准差与总体的平均数和标准差差距也不大 C、有的较大的样本的平均数和标准差与总体的平均数和标准差差距也不小 D、选取的样本容量越大，这种抽样调查的方法越科学5. 为了了解某中学(共有3个年级，每年级6个班)学生完成作业情况，可采用下列方式进行调查：①向3个年级每个班级的班长做调查；②向3个年级每个班的学习委员做调查；③向各班级每班前10名学生做调查；④将18个班级编号，从中任意抽取3个班级，向这3个班级的所有学生做调查．你认为调查具有随机性的是（ ）A、① B、② C、③ D、④6. 某环保网站正在对商店使用环保购物袋程度进行在线调查，以这个调查来作为居民支持商店使用环保购物袋程度的估计是（ ）A、合理的 B、不能确定 C、不合理的 D、以上都不对7. 随机抽取某城市30天的空气质量状况如下表，当污染指数≤100时为良，请根据以下记录估计该城市一年(以365天计)中，空气质量达到良以上的天数为 （ ）
A、216天 B、217天 C、218天 D、219天8. 某班有 位学生，每人抛 次硬币，统计正面向上次数依次为 ， ， ，…， 的人数，得到直方图（如图），记正面向上次数为 ， ， 的人数和占班级人数的比例为 ，则 的值（ ）
A、小于
B、在 与 
之间
C、在 与 
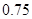之间
D、大于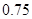
9. 某校组织400名九年级学生参加英语测试，为了解他们的测试情况（满分120分），随机抽取若干名学生，将所得成绩数据整理后，画出频数分布直方图（如图）．估计该校成绩在100～120分之间的人数有（ ）
A、12 B、48 C、60 D、7210.为了了解本校九年级学生的体能情况，随机抽查了其中30名学生，测试了1分钟仰卧起坐的次数，并绘制成如图所示的频数分布直方图，请根据图示计算，仰卧起坐次数在25～30次的频率是（ ）
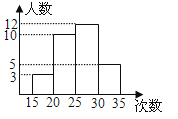A、0.1 B、0.2 C、0.3 D、0.4二、填空题
-
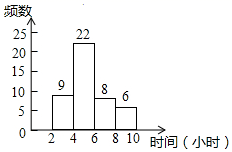
11. 为了解六年级学生掌握游泳技能的情况．在全区六年级7200名学生中，随机抽取了600名学生，结果有240名学生会游泳，那么估计该区会游泳的六年级学生数约为人．12. 某校征集校运会会徽，遴选出甲、乙、丙三种图案，为了解何种图案更受欢迎，随机调查了该校100名学生，其中68名同学喜欢甲图案，若该校共有2000人，根据所学的统计知识可以估计该校喜欢甲图案的学生有人.13. 如图是九（1）班45名同学每周课外阅读时间的频数分布直方图（每组含前一个边界值，不含后一个边界值）.其中每周课外阅读时间在6小时及以上的人有名.
14. 随着黄石市精神文明建设的不但推进，市民每天用于读书、读报、参加“全民健身运动”的时间越来越多．如图是我市晚报记者在抽样调查了一些市民用于上述活动的时间后，绘制的频率分布直方图，从左到右的前七个长方形面积之和为 ，最后一组的频数是 ，则此次抽样的样本容量是 ．
15. 在列频数分布表时，得到某数据的频数是 ，频率是 ，那么这组数据共有个．三、解答题
-
16. 某学校为了了解本校1200名学生的课外阅读的情况，现从各年级随机抽取了部分学生，对他们一周的课外阅读时间进行了调查，井绘制出如下的统计图①和图②，根据相关信息，解答下列问题：
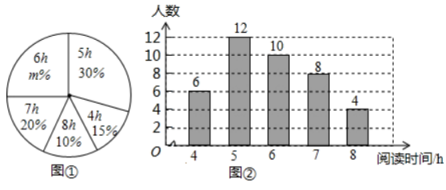
（Ⅰ）本次接受随机抽样调查的学生人数为 ， 图①中的值为 ；
（Ⅱ）求本次调查获取的样本数据的众数、中位数和平均数；
（Ⅲ）根据样本数据，估计该校一周的课外阅读时间大于的学生人数.
17.某中学学生为了解该校学生喜欢球类活动的情况，随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类)，并将调查的结果绘制成如下的两幅不完整的统计图．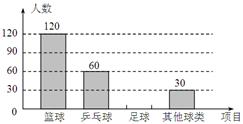
请根据图中提供的信息，解答下面的问题：
(1)参加调查的学生共有 人，在扇形图中，表示“其他球类”的扇形的圆心角为 度；
(2)将条形图补充完整；
(3)若该校有2000名学生，则估计喜欢“篮球”的学生共有 人．18.在射击竞赛的选拔赛中，运动员甲10次射击成绩的统计表和扇形统计图如下：
（1）根据统计表（图）中提供的信息，补全统计表及扇形统计图；
（2）已知乙运动员10次射击的平均成绩为9环，方差为1.2，如果只能选一人参加比赛，你认为应该派谁去？并说明理由.四、综合题
-
19. 为了科普卫生防疫知识，学校组织了一次在线知识竞赛，小佑同学分别从初二、初三两个年级随机抽取了一部分同学的成绩（百分制），并对数据（x分）进行了整理，“优秀：；良好：；合格﹔不合格：”四类分别进行统计，并绘制了如图所示的两幅统计图（不完整）.
请根据图中信息，解答下列问题：
(1)、此次共调查了名学生；(2)、扇形统计图中所在扇形的圆心角度数为；(3)、将条形统计图补充完整；(4)、若该校共有1500名学生，请你估计卫生防疫知识考核优秀的学生的人数.20. 自疫情暴发以来，我国科研团队经过不懈努力，成功地研发出了多种新冠疫苗，以下是某地甲、乙两家医院5月份某天各年龄段接种疫苗人数的频数分布表和接种总人数的形统计图：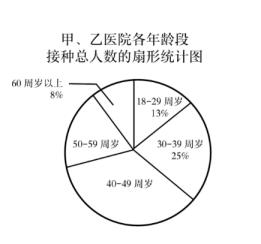
甲医院
乙医院
年龄段
频数
频率
频数
频率
18—29周岁
900
0.15
400
0.1
30—39周岁
a
0.25
1000
0.25
40—49周岁
2100
b
c
0.225
50—59周岁
1200
0.2
1200
0.3
60周岁以上
300
0.05
500
0.125
(1)、根据上面图表信息，回答下列问题：①填空：a= ， b= ， c=；
②在甲、乙两医院当天接种疫苗的所有人员中，40—49周岁年龄段人数在扇形统计图中所占圆心角为；
(2)、若A，B，C三人都于当天随机到这两家医院接种疫苗，请用列表或画树状图的方法求这三人在同一家医院接种的概率．21. 小王同学在超市进行随机抽样调查，了解人们平时喜欢用哪种方式付款，下图是根据调查结果整理出来的统计图，请据此信息完成下列问题：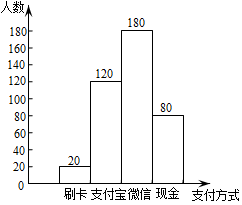
(1)、若当天该超市客流量为1.5万人，请你估计这一天使用微信支付的人数有多少人；(2)、现场调查也发现：甲、乙两人都习惯使用支付宝、微信、现金三种支付方式，并且他们选择这三种支付方式的可能性是相同的，请你利用列表或树状图计算出两人恰好选择同一种支付方式的概率．22. 新学期，某校开设了“防疫宣传心理疏导”等课程．为了解学生对新开设课程的掌握情况，从九年级学生中随机抽取了部分学生进行了一次综合测试．测试结果分为四个等级：A级为优秀，B级为良好，C级为及格，D级为不及格．将测试结果绘制了如图两幅不完整的统计图．根据统计图中的信息解答下列问题：
(1)、本次抽样测试的样本容量是；(2)、扇形统计图中A级的扇形圆心角度是 ▲ ， 并把条形统计图补充完整；(3)、该校九年级共有学生1200名，如果全部参加这次测试，估计优秀的学生是人；(4)、某班有4名优秀的同学（分别记为E、F、G、H，其中E为小明），班主任要从中随机选择两名同学进行经验分享，请利用列表法或画树状图法，求小明被选中的概率．23. 国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》，这是中国足球历史上的重大改革．为了进一步普及足球知识，传播足球文化，我市举行了“足球进校园”知识竞赛活动，为了解足球知识的普及情况，随机抽取了部分获奖情况进行整理，得到下列不完整的统计图表：获奖等次
频数
频率
一等奖
10
0.05
二等奖
20
0.10
三等奖
30
b
优胜奖
a
0.30
鼓励奖
80
0.40
请根据所给信息，解答下列问题：
(1)、a= ▲ ， b= ▲ ， 且补全频数分布直方图；(2)、若用扇形统计图来描述获奖分布情况，问获得优胜奖对应的扇形圆心角的度数是多少？(3)、在这次竞赛中，甲、乙、丙、丁四位同学都获得一等奖，若从这四位同学中随机选取两位同学代表我市参加上一级竞赛，请用树状图或列表的方法，计算恰好选中甲、乙二人的概率．