(华师大版)2022-2023学年八年级数学下册19.2 菱形 同步测试
试卷更新日期:2023-03-13 类型:同步测试
一、单选题
-
1. 如图,在平面直角坐标系中,若菱形的顶点A、B的坐标分别为 , 点D在y轴上,则点C的坐标是( )
 A、 B、 C、 D、2. 如图,菱形ABCD的对角线AC、BD相交于点O,BD=6,AC=8,E是CD的中点,则OE的长是( )
A、 B、 C、 D、2. 如图,菱形ABCD的对角线AC、BD相交于点O,BD=6,AC=8,E是CD的中点,则OE的长是( ) A、2.5 B、3 C、4 D、53. 菱形中,对角线与的长分别为6和8,则该菱形的周长为( )A、 B、20 C、 D、404. 如图,已知菱形的对角线AC;BD交于点O,E为CD的中点,若 , 则菱形的周长为( ).
A、2.5 B、3 C、4 D、53. 菱形中,对角线与的长分别为6和8,则该菱形的周长为( )A、 B、20 C、 D、404. 如图,已知菱形的对角线AC;BD交于点O,E为CD的中点,若 , 则菱形的周长为( ). A、18 B、48 C、24 D、125. 如图,在一束平行光线中插入一张对边平行的纸板,如果光线与纸板右下方所成的 , 则光线与纸板左上方所成的的度数是( )
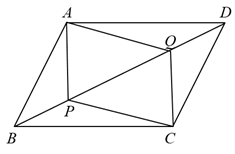
A、18 B、48 C、24 D、125. 如图,在一束平行光线中插入一张对边平行的纸板,如果光线与纸板右下方所成的 , 则光线与纸板左上方所成的的度数是( ) A、 B、 C、 D、6. 如图1,在菱形ABCD中,对角线AC、BD相交于O,要在对角线BD上找两点M、N,使得四边形AMCN是菱形,现有图2中的甲、乙两种方案,则正确的方案是( )
A、 B、 C、 D、6. 如图1,在菱形ABCD中,对角线AC、BD相交于O,要在对角线BD上找两点M、N,使得四边形AMCN是菱形,现有图2中的甲、乙两种方案,则正确的方案是( ) A、只有甲 B、只有乙 C、甲和乙 D、甲乙都不是7. 如图,在菱形ABCD中,M,N分别在AB,CD上,且 , MN与AC交于点O,连接 , 若 , 则的度数为( )
A、只有甲 B、只有乙 C、甲和乙 D、甲乙都不是7. 如图,在菱形ABCD中,M,N分别在AB,CD上,且 , MN与AC交于点O,连接 , 若 , 则的度数为( ) A、 B、 C、 D、8. 如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=28°,则∠OBC的度数为( )
A、 B、 C、 D、8. 如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=28°,则∠OBC的度数为( ) A、28° B、52° C、62° D、72°9. 如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处,易证四边形AECF是平行四边形.当∠BAE为( )度时,四边形AECF是菱形.
A、28° B、52° C、62° D、72°9. 如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处,易证四边形AECF是平行四边形.当∠BAE为( )度时,四边形AECF是菱形. A、30° B、40° C、45° D、50°10. 如图,在四边形中, , , , 点G为上一点, , 且平分 , 点E为中点,下面结论:①;②;③;④ . 其中正确的有( )
A、30° B、40° C、45° D、50°10. 如图,在四边形中, , , , 点G为上一点, , 且平分 , 点E为中点,下面结论:①;②;③;④ . 其中正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图,菱形ABCD中,对角线AC、BD相交于点O,点E为AC上一点,连接DE,AB=CE=5AE,BD=8,则DE的长为 .
 12. 在平面直角坐标系中,已知A、B、C、D四点的坐标依次为(0,0)、(6,0)、(8,6)、(2,6),若一次函数y=mx-6m的图象将四边形ABCD的面积分成1:3两部分,则m的值为 .13. 若一个菱形的两条对角线长分别为10和24,则这个菱形的边长是 .14. 已知平行四边形的一边长为3,两条对角线的长分别为4和 , 则这个平行四边形的面积为 .15. 在中,对角线和相交于点 , 若 , 则该一定是(填:矩形或正方形或菱形).
12. 在平面直角坐标系中,已知A、B、C、D四点的坐标依次为(0,0)、(6,0)、(8,6)、(2,6),若一次函数y=mx-6m的图象将四边形ABCD的面积分成1:3两部分,则m的值为 .13. 若一个菱形的两条对角线长分别为10和24,则这个菱形的边长是 .14. 已知平行四边形的一边长为3,两条对角线的长分别为4和 , 则这个平行四边形的面积为 .15. 在中,对角线和相交于点 , 若 , 则该一定是(填:矩形或正方形或菱形).三、解答题
-
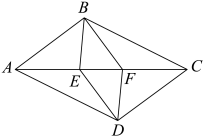
16. 如图,点P,Q是对角线上的两个点,且 , 顺次连接 , , , .
求证:四边形是平行四边形.
17. 如图,在四边形ABCD中, , 对角线BD垂直平分对角线AC;垂足为点O.求证:四边形是菱形. 18. 已知四边形ABCD,// , AD=DC=10,DB平分∠ADC,BD=12,求四边形ABCD的面积.
18. 已知四边形ABCD,// , AD=DC=10,DB平分∠ADC,BD=12,求四边形ABCD的面积.
四、综合题
-
19. 已知:如图,在中,点E,F在上,且.
 (1)、求证:四边形是平行四边形.(2)、当 , , 时,求平行四边形的面积.20. 如图,已知一次函数y=﹣x+b的图象过点A(0,3),点p是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=MP,MB=OM,OE=ON,ND=NP.
(1)、求证:四边形是平行四边形.(2)、当 , , 时,求平行四边形的面积.20. 如图,已知一次函数y=﹣x+b的图象过点A(0,3),点p是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=MP,MB=OM,OE=ON,ND=NP.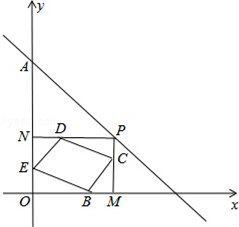 (1)、b=;(2)、求证:四边形BCDE是平行四边形;(3)、在直线y=﹣x+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,请求出所有符合的点P的坐标;若不存在,请说明理由.
(1)、b=;(2)、求证:四边形BCDE是平行四边形;(3)、在直线y=﹣x+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,请求出所有符合的点P的坐标;若不存在,请说明理由.