山西省运城市三校联考2021-2022年八年级下学期期中数学试题

试卷更新日期：2023-03-13 类型：期中考试

进入出卷网下载

一、单选题

1. 在数轴上表示不等式 $x > 1$ 的解集，正确的是（）.

A、 B、 C、 D、

查看试题解析
2. 剪纸艺术是中华民族的瑰宝，下列剪纸中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 图，线段AB经过平移得到线段 $A_{1} B_{1}$ ，若点 $A_{1} (3 ， 0)$ 、 $B_{1} (0 ， - 4)$ ， $A (- 1 ， 2)$ ，则点B的坐标为（）

A、 $(- 2 ， - 3)$ B、 $(- 4 ， - 1)$ C、 $(- 4 ， - 2)$ D、 $(- 2 ， - 2)$

查看试题解析
4. 设“▲”“●”“■”分别表示三种不同的物体，现用天平秤两次，情况如图所示，那么下列式子成立的是（）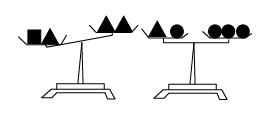

A、■＝2×● B、■＞2×● C、■＜2×● D、■＞3×●

查看试题解析
5. 如图，△COD是由△AOB绕点O按顺时针方向旋转而得，则旋转角为（）

A、∠AOD B、∠AOB C、∠BOC D、∠AOC

查看试题解析
6. 若关于x的不等式组 ${\begin{array}{l} x < 2 \\ x > a - 1 \end{array}$ 有解，则a的取值范围是（）

A、 $a \leq 3$ B、 $a < 3$ C、 $a \geq 3$ D、 $a > 3$

查看试题解析
7. 如图，△CDE是由△OAB绕着某点旋转得到的，则这点的坐标是（）

A、 $(0 ， 5)$ B、 $(0 ， 4)$ C、 $(0 ， 0)$ D、 $(1 ， 2)$

查看试题解析
8. 图，在△ABC中， $A C = B C$ ，分别以点A、C为圆心，大于 $\frac{1}{2} A C$ 的长为半径作弧，两弧相交于点M、N，作直线MN，分别交AC、BC于点D、E，连接AE，若 $∠ C = 40 °$ ，则 $∠ B A E =$ （）

A、 $20 °$ B、 $30 °$ C、 $40 °$ D、 $50 °$

查看试题解析
9. 如图，在Rt△ABC中， $∠ C = 90 °$ ， ∠BAC的平分线AD交BC于点D， $A D = 2$ ， $∠ B = 30 °$ ，则△ABD的面积是（）

A、1 B、2 C、 $\sqrt{3}$ D、 $2 \sqrt{3}$

查看试题解析
10. 在平面坐标系中，已知直线 $y = - \frac{4}{3} x + 4$ 与x轴，y轴分别交于点A、B，线段AB绕点A顺时针方向旋转 $90 °$ 得线段AC，连接BC，则C点坐标为（）

A、 $(7 ， 3)$ B、 $(6 ， 4)$ C、 $(8 ， 5)$ D、 $(8 ， 4)$

查看试题解析

二、填空题

11. 太原环城快速路大大减轻了市内道路的拥堵程度，环城快速路要求车速不得高于每小时80千米，某私家车在太原环城快速路上行驶速度为x千米/时，被抓拍了超速，则x的取值范围为．

查看试题解析
12. 命题“若 $a c^{2} > b c^{2}$ ，则 $a > b$ ”的逆命题是命题．（填“真”或“假”）

查看试题解析
13. 如图，将△OAB绕点O逆时针旋转到 $Δ O A^{'} B^{'}$ ，点B恰好落在边 $A^{'} B^{'}$ 上．已知 $∠ A B O = 60 °$ ， $A B = 7$ ， $B O = 3$ ，则 $A^{'} B$ 的长是．

查看试题解析
14. 如图，有一张直角三角形纸片，两直角边AC=6，BC=8，将△ABC折叠，使B点与A点重合，折痕为DE，则CD的长是.

查看试题解析
15. 如图，在 $△ A B C$ 中， $A B = A C$ ， $A D$ 是 $∠ B A C$ 的角平分线，交 $B C$ 于点N， $∠ E B C = ∠ B E D = 60 °$ ，若 $B E = 6$ ， $D E = 2$ ，则 $B C =$ ．

查看试题解析

三、解答题

16.

(1)、解不等式组 ${\begin{array}{l} 2 x + 1 > - 1 \\ x + 1 \leq 3 \end{array}$ ．

(2)、下面是嘉欣同学解不等式的过程，请认真阅读并完成相应任务．
$\frac{5 x + 1}{2} + 1 \geq \frac{2 x - 1}{3}$ ．
解： $3 (5 x + 1) + 6 \geq 2 (2 x - 1)$ ，第一步
$15 x + 3 + 6 \geq 4 x - 2$ ，             第二步
$15 x - 4 x ≥ - 2 - 3 - 6$ ，            第三步
$11 x \geq - 11$ ，                      第四步
$x \leq - 1$ ．                         第五步
任务一：
填空：
①以上解题过程中，第一步是依据不等式的基本性质进行变形的；
②嘉欣同学解答过程在第步出错，不正确原因是．
任务二：
请直接写出该不等式的正确解集．

查看试题解析
17. 如图，函数 $y = 3 x$ 和 $y = m x + 4$ 的图象相交于点 $A (a ， 3)$ ．

(1)、求m，a的值．

(2)、根据图象，直接写出不等式 $3 x < m x + 4$ 的解集．

查看试题解析
18. 为加快旧城改造步伐，增强城市功能，改善人居环境，我市对部分旧城区天然气管道进行改造，在改造过程中发现原有管道因弯道过多带来安全隐患，因此需要改造．某小区管道A→B改造方案如图．（实线为改造前，所有实线均互相平行或垂直，虚线为改造后）

(1)、改造前管道的长度是多少？

(2)、改造后AB之间的距离减少了多少？

查看试题解析
19. 芯片是制造汽车不可或缺的零件，某芯片厂制造的两种型号芯片的成本和批发价如表所示：该厂制造A，B两种型号芯片若干件成本为320万元，制造后立刻被汽车厂抢购一空，经会计核算后共盈利44万元．
价格型号
成本（万元/万件）
批发价（万元/万件）
A
30
34
B
35
40

(1)、芯片厂制造A，B两种型号芯片各多少万件？

(2)、由于芯片畅销，该厂计划再制造A，B两种型号芯片共30万件，其中B型号芯片的数量不多于A型号芯片数量的2倍，那么该厂制造两种型号芯片各多少件时会获得最大利润，最大利润是多少？

查看试题解析

20. 阅读与思考，请阅读下列材料，并完成相应的任务．

旋转对称图形

观察右图中的正六边形，点O是它的内角平分线的交点，将这个正六边形绕着点O旋转 $60 °$ ，旋转后的图形与旋转前的图形重合．

一般地，如果把一个图形绕着某一点旋转一定角度（小于 $360 °$ ）后，能够与原来的图形重合，那么这个图形叫做旋转对称图形，这个点叫它的对称中心．

(1)、中心对称图形旋转对称图形．（填“是”或“不是”）

(2)、下列图形中不是旋转对称图形的有，既是旋转对称图形又是中心对称图形的有，旋转72°能够完全重合的图形有．

A． B． C． D． E．

查看试题解析

21. 如图，在△ABC中， $A B = A C$ ， $∠ B + ∠ C = 60 °$ ， $B C = 9 c m$ ， ED、FG分别是AB，AC的垂直平分线，求GE的长．

查看试题解析
22. 综合与实践，如图，在Rt△ABC中， $∠ A C B = 90 °$ ， $∠ A B C = 60 °$ ， AD、CE分别是∠BAC、∠BCA的平分线，AD与CE相交于点F， $F M ⊥ B C$ 交BC于点M， $F N ⊥ A E$ 交AB于点N，连接BF．

(1)、∠EFA的度数为．

(2)、求证： $E F = D F$ ．

(3)、若 $A B = 20$ ，求CD的长．

查看试题解析
23. 与探究，如图，△ABC为等腰直角三角形，点D为斜边BC的中点，且 $B C = 4$ ，把另一个直角三角形的直角顶点放在点D处，两条直角边DM，DN分别交AB，AC于点E，F．把Rt△DMN绕点D转动，保持点E，F分别在线段AB，AC上（不与点A，B，C重合）．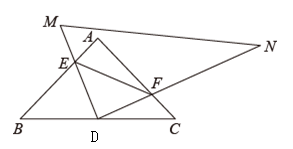

(1)、请你判断DE与DF之间的数量关系并说明理由．

(2)、求四边形DEAF的面积．

(3)、求点E、F到线段BC的距离之和．

查看试题解析

价格型号	成本（万元/万件）	批发价（万元/万件）
A	30	34
B	35	40