山西省运城市2021-2022学年八年级下学期期中数学试题

试卷更新日期：2023-03-13 类型：期中考试

进入出卷网下载

一、单选题

1. 若a＞b，则下列不等式成立的是（）

A、 $\frac{a}{3} > \frac{b}{3}$ B、a＋5＜b＋5 C、－5a＞－5b D、a－2＜b－2

查看试题解析
2. 以下冬奥会图标中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图是两个关于x的一元一次不等式的解集在同一数轴上的表示，由它们组成的不等式组的解集是（　　）

A、x＞﹣1 B、x＞2 C、x≥2 D、﹣1＜x≤2

查看试题解析
4. 在平面直角坐标系中，将线段AB平移至 $A^{'} B^{'}$ ．若点 $A (1 ， - 2)$ 的对应点 $A^{^{'}}$ 的坐标为 $(- 2 ， 3)$ ，则线段AB平移的方式可以为（）

A、向左平移3个单位，向上平移5个单位 B、向左平移5个单位，向上平移3个单位 C、向右平移3个单位，向下平移5个单位 D、向右平移5个单位，向下平移3个单位

查看试题解析

5. 小明在预习时遇到这样一道题：

例：一个等腰三角形中一角为 $30 °$ ，求这个三角形另外两角的度数．

解：如果顶角为 $30 °$ ，那么另外两角度数均为 $\frac{180 ° - 30 °}{2} = 75 °$

如果底角为 $30 °$ ，那么另外两角中，一角的度数为 $30 °$ ，另外一角的度数为 $180 ° - 30 ° \times 2 = 120 °$

这道例题体现的数学思想是（）

A、分类思想 B、统计思想 C、函数思想 D、数形结合思想

查看试题解析

6. 如图点A表示的数是-2，点B表示的数是3，点C是（与点A、B不重合）线段AB上的一点，且点C表示的数是 $\frac{3 x - 1}{2}$ ，则x的取值范围是（）

A、 $- 1 < x < \frac{7}{3}$ B、 $x < \frac{7}{3}$ C、 $x > - 1$ D、 $- \frac{7}{3} < x < 1$

查看试题解析
7. 如图，在△ABC中，DE是AC的垂直平分线，AE=3cm，△ABD的周长为13cm，则△ABC的周长为（）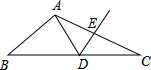

A、16cm B、13cm C、19cm D、10cm

查看试题解析
8. 如图，在 $△ A B C$ 和 $△ C D E$ 中， $∠ A C B = ∠ C E D = 90 ° ， A B = C D ， C E = A C$ ，则下列结论中错误的是（）

A、 $△ A B C ≌ △ C D E$ B、 $∠ C A B = ∠ D C E$ C、 $A B ⊥ C D$ D、E为BC中点

查看试题解析
9. 如图，一次函数y＝kx+b的图象经过点（4，-3），则关于x的不等式kx+b＜-3的解集为（）

A、x＜3 B、x＞3 C、x＜4 D、x＞4

查看试题解析
10. 如图，已知 $∠ A O B = 60 °$ ，点P在边OA上， $O P = 5 c m$ ，点M，N在边OB上， $P M = P N$ ，若 $M N = 2 c m$ ，则OM的长为（）

A、 $2 c m$ B、 $2.5 c m$ C、 $1.5 c m$ D、 $3 c m$

查看试题解析

二、填空题

11. 用不等式表示“x的2倍与3的差不小于0” ．

查看试题解析
12. 用反证法证明“三角形的三个内角中至少有一个角不小于60度”，第一步应假设．

查看试题解析
13. 某种商品进价为200元，标价300元出售，商场规定可以打折销售，但其利润不能少于5%．请你帮助售货员计算一下，此种商品可以按折销售．

查看试题解析
14. 如图，在 $△ A B C$ 中， $A C = B C ， ∠ C = 90 °$ ， AD是 $△ A B C$ 的角平分线， $D E ⊥ A B$ ，垂足为E，若 $C D = 5 c m$ ，则 $A C =$ cm．

查看试题解析
15. 如图，在 $R t △ A B C$ 中， $∠ A = 50 °$ ，将 $R t △ A B C$ 绕点B顺时针旋转，使点C落在斜边AB上的点D处，连接EA，则 $∠ A E D =$ ．

查看试题解析

三、解答题

16. 下面是小明同学解不等式的过程，请认真阅读并完成相应任务．
$\frac{2 x - 1}{3} ＞ \frac{3 x - 2}{2}$ －1.
解：2(2x－1)＞3(3x－2)－6……第一步
4x－2＞9x－6－6……第二步
4x－9x＞－6－6＋2……第三步
－5x＞－10……第四步
x＞2……第五步

(1)、任务一：填空：①以上解题过程中，第二步是依据(运算律)进行变形的；
②第步开始出现错误，这一步错误的原因是．

(2)、任务二：请直接写出该不等式的正确解集．

查看试题解析
17. 解不等式组 ${\begin{array}{l} 2 (x - 1) + 5 \geq 1 \\ 1 - \frac{x - 2}{6} > \frac{x}{3} \end{array}$ ，并写出它的非负整数解．

查看试题解析
18. 如图，正方形网格中每个小正方形的边长都是1个单位长度，每个小正方形的顶点叫做格点，已知△ABC的三个顶点都是格点，请按要求画出三角形.
（ 1 ）将△ABC先上平移1个单位长度再向右平移2个单位长度，得到△A'B'C'；
（ 2 ）将△A'B'C'绕格点O顺时针旋转90°，得到△A''B''C''.

查看试题解析
19. 为打好“蓝天、碧水、净土”三大保卫战，夏县政府决定将县城附近的烧煤取暖全部改成集中供热．某工程队承包了该项工程10000米的，总管道铺设任务．该工程队平均每天铺设管道125米，在管道铺设了20天后，为了缩短工期，经研究决定，余下的管道铺设任务要在50天内（含50天）完成，求该工程队平均每天至少再多铺设多长管道？

查看试题解析
20.

(1)、如图1，已知直线l和l上一点P，求作：直线PQ使PQ⊥l；（要求：尺规作图，保留作图痕迹，不写作法）

(2)、如图2，已知直线l和l外一点P．下面是小华设计的“过点P作直线l的垂线”的作法：请结合图形阅读作法，并将证明“PQ⊥l ”的过程补充完整作法：
①在直线l上取点A，B；②以A，B为圆心，AP，BP为半径，两弧在直线l下方交于点Q；③作直线PQ，且PQ经过点P．
证明：连接AP，AQ，BP，BQ，由作法可知，AP＝AQ， BP=BQ，
∴点A在线段PQ的垂直平分线上，点B在线段PQ的垂直平分线上，（依据：      ▲ ），
∴直线AB是线段PQ的垂直平分线（依据：      ▲ ），
∴PQ⊥l（垂直平分线的定义）．

查看试题解析
21. 如图，在 $△ A B C$ 中， $A B = A C = 2 ， ∠ B = 40 °$ ，点D在线段BC上运动（D不与B、C重合），连接AD，作 $∠ A D E = 40 °$ ， DE交线段AC于E．

(1)、点D从B向C运动时， $∠ B D A$ 逐渐变（填“大”或“小”），但 $∠ B D A$ 与 $∠ E D C$ 的度数和始终是度．

(2)、当DC的长度是多少时， $△ A B D ≌ △ D C E$ ，并说明理由．

查看试题解析
22. 4月23日是“世界读书日”，甲、乙两个书店在这一天举行了购书优惠活动．
甲书店：所有书籍按标价8折出售；
乙书店：一次购书中标价总额不超过100元的按原价计费，超过100元后的部分打6折．
以x（ $x > 100$ 单位：元）表示标价总额， $y_{甲}$ （单位：元）表示在甲书店应支付金额， $y_{乙}$ （单位：元）表示在乙书店应支付金额．

(1)、就两家书店的优惠方式，分别求 $y_{甲}$ ， $y_{乙}$ 关于x的函数表达式；

(2)、“少年正是读书时”，“世界读书日”这一天，八年级学生奇思计划去甲、乙两个书店购书，如何选择这两家书店购书更省钱？

查看试题解析
23. 综合与实践
某兴趣小组为研究特殊三角形旋转时“点、线、面”在特殊位置时的特殊结论，小组成员选取了两个完全相同的含 $30 °$ 角的三角尺如图①摆放，其中 $∠ A C B = ∠ A^{^{'}} C B^{^{'}} = 90 ° ， ∠ B = ∠ B^{^{'}} = 30 ° ， A C = A^{^{'}} C = 2$ ．保持 $△ A B C$ 不动，将 $△ A^{'} B^{'} C$ 绕着直角顶点C顺时针旋转一个角度 $α$ （ $0 ° < α \leq 120 °$ ），与边BC交于点D（如图②）．

(1)、如图②，当 $α = 30 °$ 时， $B^{'} C$ 与AB的位置关系是，判断此时 $△ A^{'} C D$ 的形状并证明．

(2)、如图③，当 $α =$ 时， $△ B^{'} C D$ 是等腰三角形．

(3)、如图④，当 $△ A^{'} B^{'} C$ 继续旋转至点 $B^{^{'}}$ 、 $A^{^{'}}$ 、B三点共线时，连接 $A B^{'}$ ，求 $A B^{'}$ 的长．

查看试题解析