山西省阳泉市盂县2021-2022学年八年级下学期期中数学试题

试卷更新日期：2023-03-13 类型：期中考试

进入出卷网下载

一、单选题

1. 已知二次根式 $\sqrt{x + 3}$ ，当x＝1时，此二次根式的值为（）

A、2 B、±2 C、4 D、±4

查看试题解析
2. 如图，一根垂直于地面的旗杆在离地面5m的B处撕裂折断，旗杆顶部落在离旗杆底部12m的A处，则旗杆折断部分AB的高度是（）

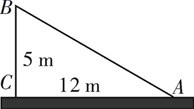A、5m B、12m C、13m D、18m

查看试题解析
3. 在平面直角坐标系中， ▱ABCD的顶点A（0，0），B（5，0），D（2，3），则顶点C的坐标是（）

A、（3，7） B、（5，3） C、（7，3） D、（8，2）

查看试题解析
4. 化简二次根式除了利用二次根式的性质外，还可以借助图形解释验证．如：化简 $\sqrt{8}$ 时，我们可以构造如图所示的图形，其中图1是一个面积为8的正方形，图2是一个面积为2的正方形，根据两图的关系我们可以得到： $\sqrt{8} = 2 \sqrt{2}$ ．这种分析问题的方法所体现的数学思想是（）

A、分类讨论 B、数形结合 C、公理化 D、类比

查看试题解析
5. 如图，在菱形ABCD中，若 $∠ A = ∠ B + 40 °$ ，则 $∠ B$ 的度数为（）．

A、110° B、70° C、55° D、35°

查看试题解析
6. 如图， $l_{1} ∥ l_{2}$ ， $A B ∥ C D$ ， $C E ⊥ l_{2}$ ， $F G ⊥ l_{2}$ ．则下列结论正确的是（）．

A、A与B之间的距离就是线段AB B、AB与CD之间的距离就是线段AC的长度 C、 $l_{1}$ 与 $l_{2}$ 之间的距离就是线段CE的长度 D、 $l_{1}$ 与 $l_{2}$ 之间的距离就是线段CD的长度

查看试题解析
7. 数学中说明某个命题不成立时常采用“举反例”，即举一个满足条件，但不满足结论的例子.为说明命题“对于任何实数a，都有 $\sqrt{a^{2}}$ ＝a”是假命题，所列举反例正确的是（）

A、a＝﹣2 B、a＝ $\frac{1}{2}$ C、a＝1 D、a＝ $\sqrt{5}$

查看试题解析
8. 如图，已知矩形 ABCD ，AD = 12， CD = 9 ，点 R 、P 分别是 DC ，BC 上的定点，点 E 、F 分别是 AP 、 RP 的中点，若CR = 4 ，则 EF =（）

A、12 B、6.5 C、9 D、不能确定

查看试题解析
9. 如图，在 $R t △ A B C$ 中， $∠ A C B$ 是直角，点D是AB边上的中点．学生写出四个结论：① $∠ A + ∠ B = 90 °$ ；② $A C^{2} + A B^{2} = B C^{2}$ ；③ $2 C D = A B$ ；④ $∠ B = 30 °$ ．上述结论中正确的是（）．

A、①②③ B、①③ C、②④ D、①②④

查看试题解析
10. 下列图形都是由同样大小的平行四边形按一定的规律组成，其中第①个图形中一共有10个平行四边形，第②个图形中一共有14个平行四边形，第③个图形中一共有19个平行四边形，……按此规律排列下去，则第⑦个图形中平行四边形的个数为（）．

A、40 B、44 C、47 D、49

查看试题解析

二、填空题

11. 写出一个你喜欢的最简二次根式．

查看试题解析
12. 如图，在平行四边形ABCD中，AB＝4，BC＝6，以点B为圆心，以任意长为半径作弧，分别交BA、BC于点P、Q，再分别以P、Q为圆心，以大于 $\frac{1}{2}$ PQ的长为半径作弧，两弧在∠ABC内交于点M，连接BM并延长交AD于点E，则DE的长为．

查看试题解析
13. 如图，吴伯伯家有一块等边三角形的空地ABC，已知E，F分别是边AB，AC的中点，量得EF=5米，他想把四边形BCFE用篱笆围成一圈放养小鸡，则需要篱笆的长是米.

查看试题解析
14. 如图，在平行四边形ABCD中，对角线AC，BD相交于点O，且 $A C ⊥ B C$ ， $A B = 10$ ， $B C = 8$ ，则平行四边形ABCD的面积为．

查看试题解析
15. 勾股定理 $a^{2} + b^{2} = c^{2}$ 本身就是一个关于a、b、c的方程，显然这个方程有无数组解，满足该方程的正整数解（a，b，c）通常叫做勾股数组．若直角三角形的边长都是正整数，则这三个数便构成一组勾股数．在学习“勾股数”的知识时，爱思考的小琦发现了一组有规律的勾股数，并将它们记录在如下的表格中：
a
6
8
10
12
14
…
b
8
15
24
35
48
…
c
10
17
26
37
50
…
则当a=20时，b+c的值为．

查看试题解析

三、解答题

16.

(1)、如图是某同学化简 $\sqrt{\frac{1}{8}}$ 的过程：
$\sqrt{\frac{1}{8}}$
$= \frac{\sqrt{1}}{\sqrt{8}}$             第一步
$= \frac{1}{2 \sqrt{2}}$             第二步
$= \frac{1 \times 2 \sqrt{2}}{2 \sqrt{2} \times \sqrt{2}}$         第三步
$= \frac{\sqrt{2}}{2}$             第四步
则最开始出现错误的步骤是，这一步错误的原因是；请直接写出化简结果；

(2)、计算： $2 \sqrt{3} - \sqrt{3} + \frac{3 \sqrt{3}}{4}$ ．

查看试题解析
17. 在直角坐标系中，我们把横、纵坐标都为整数的点称为整点，记顶点都是整点的四边形为整点四边形．如图，已知整点A（1，2），B（5，2），请在所给网格区域（不含边界）上按要求画整点四边形．

(1)、在图1中画一个以A，B，C，D为顶点的平行四边形，使AO＝CO．

(2)、在图2中画一个以A，B，C，D为顶点的平行四边形，使点C的横坐标与纵坐标的和等于点A的纵坐标的3倍．

查看试题解析
18. 如图，在菱形 $A B C D$ 中，点 $M$ 、 $N$ 分别在 $A B$ 、 $C B$ 上，且 $∠ A D M = ∠ C D N$ ，求证： $B M = B N$ ．

查看试题解析
19. 先化简，再求值： $3 (a + \sqrt{5}) (a - \sqrt{5}) - 2 a (a - 5) + 10$ ，其中 $a = \sqrt{3} - 1$ ．

查看试题解析
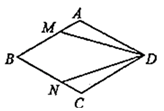20. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 6$ ， $B C = 8$ ， D、E分别是斜边AB和直角边CB上的点．把 $△ A B C$ 沿着直线DE折叠，顶点B的对应点是 $B^{'}$ ．当 $B^{'}$ 点落在直角边AC的中点上，求CE的长．

查看试题解析
21. 在一次数学课上，张老师出示了一个题目：“如图， $▱ A B C D$ 的对角线相交于点O，过点O作EF垂直于BD交AB，CD分别于点F，E，连接DF，BE．请根据上述条件，写出一个符合题意结论．”其中四位同学写出的结论如下：
小青： $O E = O F$ ；
小何：四边形DFBE是正方形；
小夏： $S_{四边形 A F E D} = S_{四边形 F B C E}$ ；
小雨： $∠ A C E = ∠ C A F$ ．
张老师说有一位同学的结论是错误的，请你指出该同学，并说明理由．

查看试题解析
22. 阅读材料，完成下列任务：
材料1：因为无理数是无限不循环小数，所以无理数的小数部分我们不可能全部写出来．比如： $π$ ， $\sqrt{2}$ 等，而常用的“…”或者“≈”的表示方法都不够百分百准确．
材料2：2.5的整数部分是2，小数部分是0.5，小数部分可以看成是 $2.5 - 2$ 得来的．
材料3：任何一个无理数，都夹在两个相邻的整数之间，如 $2 < \sqrt{5} < 3$ ，是因为 $\sqrt{4} < \sqrt{5} < \sqrt{9}$ ．
根据上述材料，回答下列问题：（参考值： $\sqrt{3} \approx 1.732$ ）

(1)、 $\sqrt{17}$ 的整数部分是，小数部分是．

(2)、 $5 + \sqrt{3}$ 也是夹在相邻两个整数之间的，可以表示为 $a < 5 + \sqrt{3} < b$ ，求 $a + b$ 的值．

(3)、已知 $3 + \sqrt{3} = x + y$ ，其中x是整数，且 $0 < y < 1$ ，求 $x + 4 y$ 的近似值（精确到0.1）．

查看试题解析
23. 实践与探究

(1)、发现：如图1，在矩形ABCD中，点E是BC的中点，将 $△ A B E$ 沿AE折叠后得到 $△ A F E$ ，点F在矩形ABCD内部，延长AF交CD于点G．猜想线段GF与GC的数量关系是

(2)、探究：
探究过程中创新小组将（1）中的“矩形ABCD”改为“平行四边形”如图2，其它条件不变，发现（1）中的结论仍然成立．并给出了推理过程如下：

证明：如图2，连接EG，

∵四边形ABCD是平行四边形，

∴ $∠ B + ∠ C = 180 °$ ， ①

即 $∠ B = 180 ° - ∠ C$ ．

∵E是BC的中点，∴ $E B = E C$ ．

∵将 $△ A B E$ 沿AE折叠后得到 $△ A F E$ ，

∴ $∠ A F E = ∠ B$ ， $E F = E B$ ．

∴ $∠ E F G = 180 ° - ∠ A F E = 180 ° - (180 ° - ∠ C) = ∠ C$ ， $E F = E C$ ．

又∵ $E G = E G$ ， ∴ $△ E F G$ ≌ $△ E C G$ ． ②

∴ ．

上述推理过程是否正确？若正确，请写出①、②步的依据，在横线上填写出结论；若错误，请给出你的证明过程；

(3)、应用：
如图3，将（1）中的“矩形ABCD”改为“正方形”，边长 $A B = 8$ ，其它条件不变，求线段GC的长．

查看试题解析

a	6	8	10	12	14	…
b	8	15	24	35	48	…
c	10	17	26	37	50	…