山西省忻州市宁武县2021-2022学年八年级下学期期中数学试题

试卷更新日期：2023-03-13 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各组数中，以a、b、c为边的三角形不是直角三角形的是（）

A、a=1.5，b=2，c=3 B、a=7，b=24，c=25 C、a=6，b=8，c=10 D、a=0.3，b=0.4，c=0.5

查看试题解析
2. 下列各式计算正确的是（）

A、 $\sqrt{6} - \sqrt{3} = \sqrt{3}$ B、 $\sqrt{12} \times \sqrt{3} = 6$ C、 $3 + \sqrt{5} = 3 \sqrt{5}$ D、 $\sqrt{10} \div 2 = \sqrt{5}$

查看试题解析
3. 如图，下面不能判断是平行四边形的是（）

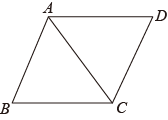A、 $∠ B = ∠ D$ ， $∠ B A D = ∠ B C D$ B、 $A B ∥ C D$ ， $A D = B C$ C、 $∠ B + ∠ D A B = 180 °$ ， $∠ B + ∠ B C D = 180 °$ D、 $A B ∥ C D$ ， $A B = C D$

查看试题解析
4. 一个圆柱形的油桶高120cm，底面直径为50cm，则桶内所能容下的最长的木棒长为（）

A、 $5 c m$ B、 $100 c m$ C、 $120 c m$ D、 $130 c m$

查看试题解析
5. 如图，在平行四边形ABCD中，过点C的直线CE⊥AB，垂足为E，若∠EAD=53°，则∠BCE的度数为（）

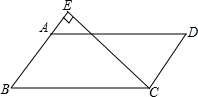A、53° B、37° C、47° D、123°

查看试题解析
6. 如图，在▱ABCD中，AD＝5，AB＝3，AE平分∠BAD交BC边于点E，则线段BE，EC的长度分别为（）

A、2和3 B、3和2 C、4和1 D、1和4

查看试题解析
7.
已知：菱形ABCD中，对角线AC与BD相交于点O，OE∥DC交BC于点E，AD=6cm，则OE的长为（　　）

A、6cm B、4cm C、3cm D、2cm

查看试题解析
8. 如图，矩形ABCD的对角线AC=8cm，∠AOD=120°，则AB的长为（）

A、 $\sqrt{3}$ cm B、2cm C、2 $\sqrt{3}$ cm D、4cm

查看试题解析
9.
如图，若圆柱的底面周长是30cm，高是40cm，从圆柱底部A处沿侧面缠绕一圈丝线到顶部B处做装饰，则这条丝线的最小长度是（　　）

A、80cm B、70cm C、60cm D、50cm

查看试题解析
10. 如图，将正方形对折后展开（图④是连续两次对折后再展开），再按图示方法折叠，能够得到一个直角三角形（阴影部分），且它的一条直角边等于斜边的一半．这样的图形有（）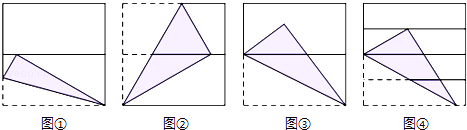

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

11. 木工做一个长方形桌面，量得桌面的长为60cm，宽为32cm，对角线为68cm，这个桌面 (填”合格”或”不合格”).

查看试题解析
12. 已知三角形三边的长分别为 $\sqrt{27}$ cm， $\sqrt{12}$ cm， $\sqrt{48}$ cm，则它的周长为cm.

查看试题解析
13. 如图，在▱ABCD中，E，F是对角线BD上的两点，要使四边形AFCE是平行四边形，则需添加的一个条件可以是．（只添加一个条件）

查看试题解析
14. 如图，矩形ABCD沿AE折叠，使D点落在BC边上的F点处，若∠BAF＝58°，则∠DAE等于度．

查看试题解析
15. 已知平行四边形ABCD中，AB＝4，BC＝6，BC边上的高AE＝2，AF⊥DC于F，则DF的长是．

查看试题解析

三、解答题

16. 计算：

(1)、 $\frac{\sqrt{75} \times \sqrt{27}}{\sqrt{12}} - 2$

(2)、 $(\frac{\sqrt{3}}{2} + \sqrt{8}) (\sqrt{8} - \frac{\sqrt{3}}{2})$

(3)、 $(\sqrt{48} + \frac{\sqrt{6}}{4}) \div \sqrt{27}$

查看试题解析
17. 拦河坝的横断面是梯形，如图，其上底是 $\sqrt{8}$ m，下底是 $\sqrt{32}$ m，高是 $\sqrt{3}$ m.

(1)、求横断面的面积；

(2)、若用300 m³的土，可修多长的拦河坝？

查看试题解析
18. 如图，小旭放风筝时，风筝线断了，风筝挂在了树上．他想知道风筝距地面的高度．于是他先拉住风筝线垂直到地面上，发现风筝线多出1米，然后把风筝线沿直线向后拉开5米，发现风筝线末端刚好接触地面(如右图为示意图)．请你帮小旭求出风筝距离地面的高度AB．

查看试题解析
19. 如图是一块四边形木板，其中 $A B = 16 cm$ ， $B C = 24 cm$ ， $C D = 9 cm$ ， $A D = 25 cm$ ， $∠ B = ∠ C = 90 °$ ．李师傅找到 $B C$ 边的中点 $P$ ，连接 $A P$ ， $D P$ ，发现 $△ A P D$ 是直角三角形．请你通过计算说明理由．

查看试题解析
20. 如图，O为矩形 $A B C D$ 对角线的交点， $D E / / A C$ ， $C E / / B D$ ．

(1)、求证：四边形 $O C E D$ 是菱形；

(2)、若 $A B = 3$ ， $B C = 4$ ，求四边形 $O C E D$ 的面积．

查看试题解析
21. 如图，四边形ABCD是正方形，BE⊥BF，BE=BF，EF与BC交于点G．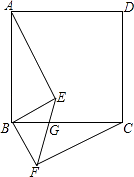

(1)、求证：AE=CF；

(2)、若∠ABE=55°，求∠EGC的大小．

查看试题解析
22. 阅读理解：
课堂上学习了勾股定理后，知道“勾三、股四、弦五”．王老师给出一组数让学生观察：3，4，5；5，12，13；7，24，25；9，40，41；……学生发现这些勾股数的勾都是奇数，且从3起就没有间断过，于是王老师提出以下问题让学生解决．

(1)、请你根据上述的规律写出下一组勾股数：11，，；

(2)、若第一个数用字母a（a为奇数，且 $a \geq 3$ ）表示，则后两个数用含a的代数式分别怎么表示？聪明的小明发现每组第二个数有这样的规律： $4 = \frac{3^{2} - 1}{2}$ ， $12 = \frac{5^{2} - 1}{2}$ ， $24 = \frac{7^{2} - 1}{2}$ ， ……于是他很快表示出了第二个数为 $\frac{a^{2} - 1}{2}$ ，则用含a的代数式表示第三个数为．

(3)、用所学知识说明（2）中用a表示的三个数是勾股数．

查看试题解析
23. 操作与证明：如图1，把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起，使三角板的直角顶点和正方形的顶点C重合，点E、F分别在正方形的边CB、CD上，连接AF；取AF中点M，EF的中点N，连接MD，MN．

(1)、连接AE，求证：△AEF是等腰三角形；

(2)、猜想与发现：
在（1）的条件下，请判断MD、MN的数量关系和位置关系，得出结论．
结论1：DM、MN的数量关系是；
结论2：DM、MN的位置关系是；

(3)、拓展与探究：
如图2，将图1中的直角三角板ECF绕点C顺时针旋转180°，其他条件不变，则（2）中的两个结论还成立吗？若成立，请加以证明；若不成立，请说明理由．

查看试题解析