山西省太原市2021-2022学年八年级下学期期中数学试题
试卷更新日期:2023-03-13 类型:期中考试
一、单选题
-
1. 2022年3月5日,李克强总理在政府工作报告中提出,今年发展主要预期目标之一是粮食产量保持在1.3万亿斤以上.若用x(万亿斤)表示我国今年粮食产量,则x满足的关系为( )A、 B、 C、 D、2. 下面是全国一体化在线政务服务平台中四个省级小程序的图标,其中的图案是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,是等边三角形,点E,F分别在AB,AC边上,且 . 若 , 则EF的长为( )
3. 如图,是等边三角形,点E,F分别在AB,AC边上,且 . 若 , 则EF的长为( ) A、6 B、4 C、3 D、24. 在不等式的两边同时除以-6,得到的不等式为( )A、 B、 C、 D、5. 用反证法证明“一个三角形中不能有两个角为直角”时,应先作出的假设是( )A、一个三角形中不能有两个角为锐角 B、一个三角形中不能有两个角为钝角 C、一个三角形中能有两个角为直角 D、一个三角形中能有两个角为锐角6. 将不等式与的解集表示在同一数轴上正确的是( )A、
A、6 B、4 C、3 D、24. 在不等式的两边同时除以-6,得到的不等式为( )A、 B、 C、 D、5. 用反证法证明“一个三角形中不能有两个角为直角”时,应先作出的假设是( )A、一个三角形中不能有两个角为锐角 B、一个三角形中不能有两个角为钝角 C、一个三角形中能有两个角为直角 D、一个三角形中能有两个角为锐角6. 将不等式与的解集表示在同一数轴上正确的是( )A、 B、
B、 C、
C、 D、
D、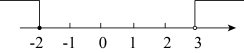 7. 如图,线段CD是由线段AB绕点O顺时针旋转得到的,其中点A,B的对应点分别是点C,D,则下列各角中等于旋转角的是( )
7. 如图,线段CD是由线段AB绕点O顺时针旋转得到的,其中点A,B的对应点分别是点C,D,则下列各角中等于旋转角的是( ) A、 B、 C、 D、8. 如图,一次函数与的图象相交于点 , 则不等式的解集为( )
A、 B、 C、 D、8. 如图,一次函数与的图象相交于点 , 则不等式的解集为( ) A、 B、 C、 D、9. 如图,中, , 将沿BC方向平移得到 , 其中A,B,C的对应点分别是点D,E,F,DE与AC交于点G.若点E是BC的中点,则下列结论中不一定正确的是( )
A、 B、 C、 D、9. 如图,中, , 将沿BC方向平移得到 , 其中A,B,C的对应点分别是点D,E,F,DE与AC交于点G.若点E是BC的中点,则下列结论中不一定正确的是( )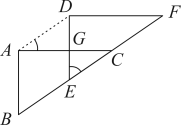 A、 B、 C、AC与DE互相垂直平分 D、10. 3月4日,太原市住建局宣布,本市2022年计划改造老旧小区604个,涉及户数11.6万户.某小区计划在改造时给80户住户安装天然气,住户需共同承担整体初装费30000元,另需缴纳入户费500元/户.根据惠民政策,政府给予该小区住户一定的补贴,这样平均每户的实际费用不超过800元.若设政府给每户的补贴为x元,则x满足的不等式为( )
A、 B、 C、AC与DE互相垂直平分 D、10. 3月4日,太原市住建局宣布,本市2022年计划改造老旧小区604个,涉及户数11.6万户.某小区计划在改造时给80户住户安装天然气,住户需共同承担整体初装费30000元,另需缴纳入户费500元/户.根据惠民政策,政府给予该小区住户一定的补贴,这样平均每户的实际费用不超过800元.若设政府给每户的补贴为x元,则x满足的不等式为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 不等式的最大整数解为 .12. 点P(2,﹣3)与点P′关于原点成中心对称,则P′的坐标为 .13. 如图,中, , 则的面积为 .
 14. 如图,将绕点A逆时针旋转70°,得到 , 若点B的对应点D在线段BC的延长线上,则的度数为°,
14. 如图,将绕点A逆时针旋转70°,得到 , 若点B的对应点D在线段BC的延长线上,则的度数为°,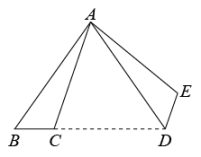
三、解答题
-
15. 已知中,于点D,AE平分 , 交CD于点F.
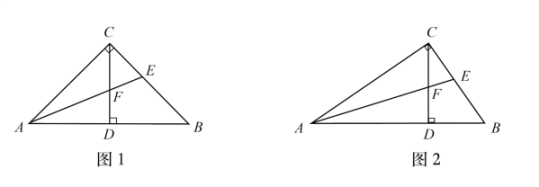
请从A,B两题中任选一题作答.我选择题.A.如图1,若 , 则CF的长为 .
B.如图2,若 , 则DF的长为 .
16. 解不等式组 .17. 如图,平面直角坐标系中,各顶点的坐标依次为 . (1)、将先向左平移2个单位长度,再向上平移6个单位长度得到 .
(1)、将先向左平移2个单位长度,再向上平移6个单位长度得到 .①请在图中画出;
②点的坐标可以看成是点A,B,C的横坐标分别_▲ 、纵坐标分别 ▲ 得到的;
③也可以看成是沿的方向一次平移_▲ 个单位长度得到;
(2)、将点A,B,C的横,纵坐标分别乘-1,依次得到点;①请在图中画出
②请写出与的位置关系:_▲
18. 下面是小彬求解一元一次不等式及自我检查的过程,请认真阅读并完成相应的任务.解答过程
自我检查
解:去分母,得 . …第一步去括号,得 . …第二步
移项,得 . …第三步
合并同类项,得 . …第四步
系数化为1,得 . …第五步
第一步正确,其依据是____;
第二步符合去括号法则,也正确;
第三步出错了!
(1)、第一步的依据是不等式的一条性质,请写出这一性质的内容:(2)、第三步出错的原因是:;(3)、请从第三步开始,写出正确解答过程.19. 为确保“双减”落地,某校在课后服务中开设了丰富多彩的选修课.面塑组的同学精心制作了一批“冰墩墩•雪容融”面偶,在校园义卖中大受欢迎.已知面偶的义卖价格如下表所示(大小面偶均整对出售),八年级一班的同学集资300元,计划购买大,小号“冰墩墩•雪容融”面偶共25对,他们最多能买多少对大号面偶?
类型
大号
小号
价格
15元/对
10元/对
20. 已知:如图,中,点D是BC的中点,于点E.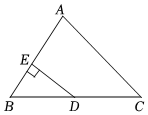 (1)、求作:射线DF,使于点F(要求:尺规作图,保留作图痕迹,不写作法;如果完成有困难,可画出草图后解答(2)题);(2)、在(1)得到的图中,若 , 求证: .21. 我市晋源区积极推广“鱼混+”综合种养模式,探索鱼+稻,莲、花、果、菜的生态化养殖.近日,“鱼菜混养”示范基地的一批鲈鱼上市,定价为40元千克,基地对购买量在100~300千克(含100与300千克)的本地客户有两种付款方案(客户只能选择其中一种方案);
(1)、求作:射线DF,使于点F(要求:尺规作图,保留作图痕迹,不写作法;如果完成有困难,可画出草图后解答(2)题);(2)、在(1)得到的图中,若 , 求证: .21. 我市晋源区积极推广“鱼混+”综合种养模式,探索鱼+稻,莲、花、果、菜的生态化养殖.近日,“鱼菜混养”示范基地的一批鲈鱼上市,定价为40元千克,基地对购买量在100~300千克(含100与300千克)的本地客户有两种付款方案(客户只能选择其中一种方案);方案甲:按定价出售,由基地免费送货;方案乙:售价打八折,但客户需支付运费1200元.
(1)、请分别写出按方案甲、方案乙购买这种鲈鱼的应付款(元),(元)与购买量x(千克)之间的函数关系式及x的取值范围;(2)、这类客户选择哪种付款方案更合算?说明理由.22. 下面是小颖证明命题“在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半”的过程,请阅读后完成相应任务.已知:如图1,中, .
求证:____
证明:延长BC到点D,使 , 连接AD.
∵ ,
∴
∵ ,
∴ . ∴ .
∴是等边三角形.(依据:____)
∴ , ∴ .
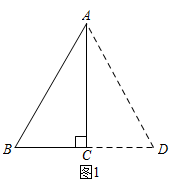 (1)、上述过程中,求证的结论为;括号中的依据为;(2)、证明以上命题后,小颖运用它解决了下列问题.
(1)、上述过程中,求证的结论为;括号中的依据为;(2)、证明以上命题后,小颖运用它解决了下列问题.请从A,B两题中任选一题补全图形并作答.我选择题.
如图2,在中, , 点E是AB的中点.
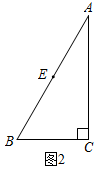
A.过点E作EF垂直于AC,垂足为点F,求EF的长.
B.过点E作EF垂直于AB,垂足为点E,交AC于点F,求EF的长.
23. 综合与实践问题情境:活动课上,同学们以等腰三角形为背景展开有关图形旋转的探究活动,如图1,已知甲; , . 有从图1的位置开始绕点A逆时针旋转,得到(点D,E分别是点B,C的对应点),旋转角为 , 设线段AD与BC相交于点M,线段DE分别交BC,AC于点O,N
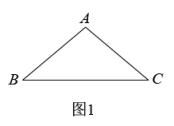

 (1)、特例分析:如图2,当旋转到时,旋转角的度数为°;(2)、探究规律:如图3,在绕点A逆时针旋转的过程中,“求真”小组的同学发现线段AM始终等于线段AN,请你证明这一结论;(3)、拓展延伸:请从A,B两题中任选一题作答.我选择题
(1)、特例分析:如图2,当旋转到时,旋转角的度数为°;(2)、探究规律:如图3,在绕点A逆时针旋转的过程中,“求真”小组的同学发现线段AM始终等于线段AN,请你证明这一结论;(3)、拓展延伸:请从A,B两题中任选一题作答.我选择题A.直接写出当是等腰三角形时旋转角的度数.
B.在图3中.作直线BD,CE交于点P.请补全图形,并直接写出当是直角三角形时旋转角的度数.