山西省吕梁市交城县2021-2022学年八年级下学期期中数学试题
试卷更新日期:2023-03-13 类型:期中考试
一、单选题
-
1. 若式子在实数范围内有意义,则a的取值范围是( ).A、 B、 C、 D、2. 下列各式中是最简二次根式的是( )A、 B、 C、 D、3. 下列选项中,能构成等腰直角三角形的是( )A、 , , 1 B、3,3,5 C、 , , D、3,4,4. 下列运算正确的是( ).A、 B、 C、 D、5. 如图,在△ABC中,∠C=90°,AC=4,BC=8,D,E分别是AC,BC的中点,则DE的长是( )
 A、4 B、5 C、 D、6. 勾股定理是一个古老的数学定理,它有很多种证明方法.下面四幅几何图形中,不能用于证明勾股定理的是( )A、
A、4 B、5 C、 D、6. 勾股定理是一个古老的数学定理,它有很多种证明方法.下面四幅几何图形中,不能用于证明勾股定理的是( )A、 B、
B、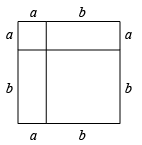 C、
C、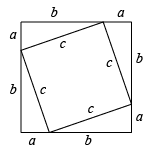 D、
D、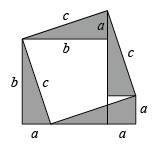 7. 下列命题中正确的是( )A、对角线互相垂直的四边形是菱形 B、邻边相等的平行四边形是正方形 C、矩形的对角线相等且互相垂直 D、正方形的面积等于对角线平方的一半8. 如图,A(6,0),B(-4,0),以A为圆心,AB为半径画弧,交轴正半轴于点C,则点C的坐标为( )
7. 下列命题中正确的是( )A、对角线互相垂直的四边形是菱形 B、邻边相等的平行四边形是正方形 C、矩形的对角线相等且互相垂直 D、正方形的面积等于对角线平方的一半8. 如图,A(6,0),B(-4,0),以A为圆心,AB为半径画弧,交轴正半轴于点C,则点C的坐标为( ) A、(0,8) B、(8,0) C、(0,10) D、(10,0)9. 如图,△ABC中,AB=AC,点D在BC的延长线上,连接AD.点E,F分别是BC,AD的中点.若EF=3,则AD的长为( )
A、(0,8) B、(8,0) C、(0,10) D、(10,0)9. 如图,△ABC中,AB=AC,点D在BC的延长线上,连接AD.点E,F分别是BC,AD的中点.若EF=3,则AD的长为( ) A、3 B、 C、6 D、10. 如图,已知矩形纸片ABCD中,AB=15,AD=10,点E在BC边上,将△ABE沿BE折叠,点A落在点F处,此时点F到CD的距离为1,到AD的距离为3,则AE的长为( )
A、3 B、 C、6 D、10. 如图,已知矩形纸片ABCD中,AB=15,AD=10,点E在BC边上,将△ABE沿BE折叠,点A落在点F处,此时点F到CD的距离为1,到AD的距离为3,则AE的长为( ) A、4 B、5 C、6 D、8
A、4 B、5 C、6 D、8二、填空题
-
11. 计算 的结果是 .12. 现有两根长度为2cm和cm的小棒,要利用这两根小棒作边围成直角三角形,则所需第三根小棒的长可以是cm.13. 如图,在正方形网格中,点A,B,C,D,E是格点,则∠ABD+∠CBE的度数为 .
 14. 如图,在平行四边形ABCD中,AD= , 点E在AB上,DE平分∠ADC,CE平分∠BCD,则的值为 .
14. 如图,在平行四边形ABCD中,AD= , 点E在AB上,DE平分∠ADC,CE平分∠BCD,则的值为 . 15. 如图,在正方形ABCD中,点E为BC上一点,FG⊥AE交AB于点F,交CD于点G,垂足为O,连接OD.若BE=1,FG= , ∠ODA=2∠BAE,则OD的长为 .
15. 如图,在正方形ABCD中,点E为BC上一点,FG⊥AE交AB于点F,交CD于点G,垂足为O,连接OD.若BE=1,FG= , ∠ODA=2∠BAE,则OD的长为 .
三、解答题
-
16. 计算:(1)、(2)、17. 若最简二次根式与可以合并.(1)、求a的值;(2)、对于任意不相等的两个数x,y,定义一种运算“※”如下:x※y= , 如:3※2== . 请求a※[a※(-2)]的值.18. 如图,在△ABC中,AB:CB:CA=3:4:5,且周长为72cm,点M以每秒2cm的速度从A向B运动,点N以每秒3cm的速度从B向C运动,如果两点同时出发,经过4秒时,△BMN的面积为多少?
 19. 如图,在平行四边形ABCD中,点E为AB上一点,且∠CDE=∠DCB.
19. 如图,在平行四边形ABCD中,点E为AB上一点,且∠CDE=∠DCB. (1)、求证:AD=DE;(2)、请判断BD与CE的数量关系,并说明理由.20. 如图,折叠矩形纸片ABCD,使点C与点A重合,EF为折痕,点D的对称点为D′,连接CE.
(1)、求证:AD=DE;(2)、请判断BD与CE的数量关系,并说明理由.20. 如图,折叠矩形纸片ABCD,使点C与点A重合,EF为折痕,点D的对称点为D′,连接CE. (1)、求证:四边形AFCE是菱形;(2)、若AB=3,BC=9,求四边形ABCD′的面积.21. 阅读下面的材料,并解决问题.(1)、观察上式并填空:=;(2)、观察上述规律并猜想:当n是正整数时:=(用含的式子表示)(3)、请利用(2)的结论计算:22.
(1)、求证:四边形AFCE是菱形;(2)、若AB=3,BC=9,求四边形ABCD′的面积.21. 阅读下面的材料,并解决问题.(1)、观察上式并填空:=;(2)、观察上述规律并猜想:当n是正整数时:=(用含的式子表示)(3)、请利用(2)的结论计算:22. (1)、图1是由有20个边长为1的正方形组成的,把它按图1的分割方法分割成5部分后可拼接成一个大正方形(内部的粗实线表示分割线),请你在图2的网格中画出拼接成的大正方形.(2)、如果(1)中分割成的直角三角形两直角边分别为a,b斜边为c.请你利用图2中拼成的大正方形证明勾股定理.(3)、应用:测量旗杆的高度:校园内有一旗杆,小希想知道旗杆的高度,经观察发现从顶端垂下一根拉绳,于是他测出了下列数据:①测得拉绳垂到地面后,多出的长度为0.5米;②他在距离旗杆4米的地方拉直绳子,拉绳的下端恰好距离地面0.5米.请你根据所测得的数据设计可行性方案,解决这一问题.(画出示意图并计算出这根旗杆的高度).23. 如图1,四边形ABCD是矩形,对角线AC,BD交于点O,点E是OA的中点,点F是OC的中点,连接BE,DE,BF,DF.
(1)、图1是由有20个边长为1的正方形组成的,把它按图1的分割方法分割成5部分后可拼接成一个大正方形(内部的粗实线表示分割线),请你在图2的网格中画出拼接成的大正方形.(2)、如果(1)中分割成的直角三角形两直角边分别为a,b斜边为c.请你利用图2中拼成的大正方形证明勾股定理.(3)、应用:测量旗杆的高度:校园内有一旗杆,小希想知道旗杆的高度,经观察发现从顶端垂下一根拉绳,于是他测出了下列数据:①测得拉绳垂到地面后,多出的长度为0.5米;②他在距离旗杆4米的地方拉直绳子,拉绳的下端恰好距离地面0.5米.请你根据所测得的数据设计可行性方案,解决这一问题.(画出示意图并计算出这根旗杆的高度).23. 如图1,四边形ABCD是矩形,对角线AC,BD交于点O,点E是OA的中点,点F是OC的中点,连接BE,DE,BF,DF. (1)、求证:四边形BEDF为平行四边形;(2)、如图2,延长BE到点G使EG=BE,连接DG,请判断四边形EGDF是什么特殊四边形?并说明你的理由;(3)、请在图2中连接BF,GF,试探究当∠AOB的大小满足什么条件时,BF=GF?请说明你的理由.
(1)、求证:四边形BEDF为平行四边形;(2)、如图2,延长BE到点G使EG=BE,连接DG,请判断四边形EGDF是什么特殊四边形?并说明你的理由;(3)、请在图2中连接BF,GF,试探究当∠AOB的大小满足什么条件时,BF=GF?请说明你的理由.