山西省临汾市尧都区2021-2022学年八年级下学期期中数学试题
试卷更新日期:2023-03-13 类型:期中考试
一、单选题
-
1. 下列式子中,是最简二次根式的是( )A、 B、 C、 D、2. 下面性质中,平行四边形不一定具备的是( )A、邻角互补 B、邻边相等 C、对边平行 D、对角线互相平分3. 若 , 则a的取值范围是( )A、 B、 C、 D、4. 如图,在矩形中,对角线、交于点O, , 以下说法错误的是( )
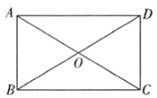 A、 B、 C、 D、5. 以下各组数据为三边的三角形中,是直角三角形的是( )A、4,2,3 B、3,5,7 C、5,7,9 D、6,8,106. 如图所示,某居民小区为了美化居住环境,要在一块三角形空地上围一个四边形花坛.已知四边形的顶点分别是边的中点,量得米, , 则四边形花坛的周长是( )
A、 B、 C、 D、5. 以下各组数据为三边的三角形中,是直角三角形的是( )A、4,2,3 B、3,5,7 C、5,7,9 D、6,8,106. 如图所示,某居民小区为了美化居住环境,要在一块三角形空地上围一个四边形花坛.已知四边形的顶点分别是边的中点,量得米, , 则四边形花坛的周长是( )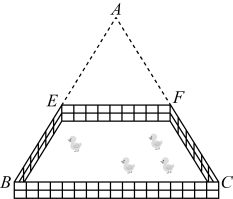 A、24米 B、32米 C、40米 D、48米7. 如图,一轮船M以12海里/时的速度从港口A出发向东北方向航行,一小时后另一轮船N以7海里/时的速度从港口A出发向东南方向航行,又过了一个小时后,两船的距离为( )
A、24米 B、32米 C、40米 D、48米7. 如图,一轮船M以12海里/时的速度从港口A出发向东北方向航行,一小时后另一轮船N以7海里/时的速度从港口A出发向东南方向航行,又过了一个小时后,两船的距离为( )
 A、海里 B、24海里 C、25海里 D、海里8. 元宵节是我国的传统文化节日,做花灯、赏花灯是传统节日中的重要活动内容.小明在完成综合实践活动做花灯的过程中,花灯底部需要做一个对角线互相垂直的矩形铁丝网固定花灯的形状,该矩形铁丝网的面积为 , 则底部一条对角线所用的铁丝至少需( )
A、海里 B、24海里 C、25海里 D、海里8. 元宵节是我国的传统文化节日,做花灯、赏花灯是传统节日中的重要活动内容.小明在完成综合实践活动做花灯的过程中,花灯底部需要做一个对角线互相垂直的矩形铁丝网固定花灯的形状,该矩形铁丝网的面积为 , 则底部一条对角线所用的铁丝至少需( ) A、 B、 C、 D、9. 已知是一个正整数,则正整数a的最小值为( )A、0 B、6 C、3 D、210. 如图,矩形的两条边 , 分别落在x轴、y轴上,A点坐标为 , B点坐标为 , 点D在线段上,沿直线将矩形折叠,使点C与y轴上的点E重合,则点D的坐标为( )
A、 B、 C、 D、9. 已知是一个正整数,则正整数a的最小值为( )A、0 B、6 C、3 D、210. 如图,矩形的两条边 , 分别落在x轴、y轴上,A点坐标为 , B点坐标为 , 点D在线段上,沿直线将矩形折叠,使点C与y轴上的点E重合,则点D的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 一个直角三角形的最长边为4,最短边为3,则第三边为 .12. 能与合并的最简二次根式是 .13. 如图,在中,过点C作 , 垂足为E,若 , 则的度数为 .
 14. 山西某高校举办帐篷节,举办方设计旗帜如图1所示,旗帜可简化如图2,在中, , , , 则的长度为 .
14. 山西某高校举办帐篷节,举办方设计旗帜如图1所示,旗帜可简化如图2,在中, , , , 则的长度为 .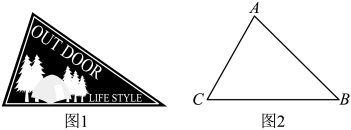 15. 如图,边长为8的菱形两条对角线相交于点O,以为斜边向外作 , 连接 , 则线段长度的最大值为 .
15. 如图,边长为8的菱形两条对角线相交于点O,以为斜边向外作 , 连接 , 则线段长度的最大值为 .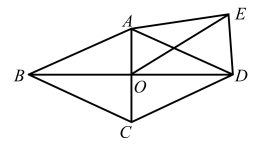
三、解答题
-
16.(1)、 .(2)、下面是小明同学对于题目“化简并求值: , 其中”的解答过程,请认真阅读并完成相应任务.
解:原式第一步
第二步
第三步
把代入得,原式第四步
任务一:填空:第步开始出现错误,错误原因是 .
任务二:请直接写出代数式正确的值.
17. 如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画出图形. (1)、在图1中,画一个以为边,面积是6的平行四边形.(2)、在图2中,画一个以斜边的等腰直角三角形.18. 某居民小区有块形状为矩形的绿地,长为米,宽为米,现在要矩形绿地中修建两个形状大小相同的长方形花坛(即图中阴影部分),每个长方形花坛的长为米,宽为米.
(1)、在图1中,画一个以为边,面积是6的平行四边形.(2)、在图2中,画一个以斜边的等腰直角三角形.18. 某居民小区有块形状为矩形的绿地,长为米,宽为米,现在要矩形绿地中修建两个形状大小相同的长方形花坛(即图中阴影部分),每个长方形花坛的长为米,宽为米. (1)、求矩形的周长.(结果化为最简二次根式)(2)、除去修建花坛的地方,其它地方全修建成通道,通道上要铺上造价为6元/平方米的地砖,要铺完整个通道,则购买地砖需要花费多少元?19. 如图,是平行四边形的一条对角线,E是的中点,连接并延长交的延长线于F.
(1)、求矩形的周长.(结果化为最简二次根式)(2)、除去修建花坛的地方,其它地方全修建成通道,通道上要铺上造价为6元/平方米的地砖,要铺完整个通道,则购买地砖需要花费多少元?19. 如图,是平行四边形的一条对角线,E是的中点,连接并延长交的延长线于F. (1)、求证: .(2)、当时,求证:四边形是矩形.20. 阅读与思考:请阅读下列材料,并完成相应的任务.
(1)、求证: .(2)、当时,求证:四边形是矩形.20. 阅读与思考:请阅读下列材料,并完成相应的任务.若直角三角形的三边的长都是正整数,则三边的长为“勾股数”.构造勾股数,就是要寻找3个正整数,使它们满足“其中两个数的平方和(或平方差)等于第三个数的平方”.通过观察常见勾股数“3,4,5”;“5,12,13”;“7,24,25”……猜想当一组勾股数中(),最小数a为奇数时,另两个正整数b和c满足比且 , 解得 , . 任务:
(1)、请证明猜想成立,即证明 , , 构成勾股数.(2)、若一组勾股数中,最小数为9,则另两个数分别是和 .21. 如图,在中, , , . 点E从点B出发沿方向以每秒1个单位的速度向点A匀速运动,同时点D从点C出发沿方向向点A匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒().过点D作交于点F,连接、 .
请问:
(1)、若 , 请问点D每秒运动多少个单位时,四边形是平行四边形?(2)、若四边形为菱形,此时t= , 点D每秒运动个单位.(请直接写出结果,不说明理由)22. 综合与实践:在学习二次根式时,发现一些含有根号的式子可以结合完全平方式化成另一个式子的平方,如: ,.
由此,可将一些被开方数为无理数的式子进行化简 , .
(1)、请你依上述方法将化成一个式子的平方,并直接写出的值.(2)、化简: .(3)、若且a、m、n均为正整数,则a= .23. 综合与探究:如图1,四边形中,E、F、G、H分别是、、、的中点,顺次连接E、F、G、H. (1)、猜想四边形的形状是(直接回答,不必说明理由).(2)、如图2,P在四边形内一点,使 , , , 其他条件不变,试探究四边形的形状,并说明理由.(3)、在(2)的条件下, , , , , 求四边形的面积.
(1)、猜想四边形的形状是(直接回答,不必说明理由).(2)、如图2,P在四边形内一点,使 , , , 其他条件不变,试探究四边形的形状,并说明理由.(3)、在(2)的条件下, , , , , 求四边形的面积.