山西省晋中市介休市2021-2022学年八年级下学期期中数学试题

试卷更新日期：2023-03-13 类型：期中考试

进入出卷网下载

一、单选题

1. 若 $m > n$ ，则下列不等式不一定成立的是（）

A、 $m + 3 > n + 3$ B、 $2 m > 2 n$ C、 $\frac{m}{3} > \frac{n}{3}$ D、 $m^{2} > n^{2}$

查看试题解析
2. 在下列现象中，属于平移的是（）．

A、荡秋千运动 B、月亮绕地球运动 C、操场上红旗的飘动 D、教室可移动黑板的左右移动

查看试题解析
3. 不等式 $x + 1 \geq 2 x - 1$ 的解集在数轴上表示正确的是（）．

A、 B、 C、 D、

查看试题解析
4. 如图，在正方形网格中，△MPN绕某一点旋转某一角度得到△M′P′N′，则旋转中心可能是（　　）

A、点A B、点B C、点C D、点D

查看试题解析
5. 不等式组 ${\begin{array}{l} x + 5 \leq 0 \\ \frac{3 x - 1}{2} \geq 2 x + 1 \end{array}$ 的最大负整数解为（）

A、 $- 2$ B、 $- 3$ C、 $- 4$ D、 $- 5$

查看试题解析
6. 如图，在Rt△ABC中，∠C=90°，AC=12，BC=18，DE是线段AB的垂直平分线，则BD的长为（）

A、8 B、10 C、13 D、15

查看试题解析
7. 图，方格纸中的△ABC经过变换，可以得到△A₁B₁C₁ ，则正确的变换方法是（）

A、将△ABC向右平移5格 B、将△ABC向右平移5格，再向下平移4格 C、将△ABC绕点C按逆时针方向旋转90°后，再向下平移3格 D、将△ABC绕点C按顺时针方向旋转90°后，再向下平移3格

查看试题解析
8. 如图，螳螂亦称刀螂，无脊椎动物，属肉食性昆虫．在螳螂的示意图中，AB∥DE， $△ A B C$ 是等腰三角形， $∠ A B C = 124 °$ ， $∠ C D E = 72 °$ ，则 $∠ A C D$ 的度数为（）

A、16° B、28° C、44° D、45°

查看试题解析
9. 某单位为响应政府号召，需要购买分类垃圾桶6个，市场上有A型和B型两种分类垃圾桶，A型分类垃圾桶500元/个，B型分类垃圾桶550元/个，总费用不超过3100元，则不同的购买方式有（）

A、2种 B、3种 C、4种 D、5种

查看试题解析
10. 图1是一个地铁站入口的双翼闸机.如图2，它的双翼展开时，双翼边缘的端点A与B之间的距离为10cm，双翼的边缘AC＝BD＝54cm，且与闸机侧立面夹角∠PCA＝∠BDQ＝30°.当双翼收起时，可以通过闸机的物体的最大宽度为（）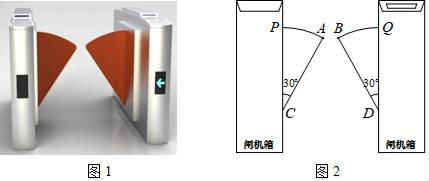

A、(54 $\sqrt{3}$ +10) cm B、(54 $\sqrt{2}$ +10) cm C、64 cm D、54cm

查看试题解析

二、填空题

11. 如果关于x的不等式x≥ $\frac{a - 1}{2}$ 的解集在数轴上表示如图所示，那么a的值为．

查看试题解析
12. 小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．如图：一把直尺压住射线OB，另一把直尺压住射线OA并且与第一把直尺交于点P，小明说：“射线OP就是∠BOA的角平分线．”小明的做法，其理论依据是

查看试题解析
13. 如图，一次函数 $y = - x - 2$ 与 $y = k x + b$ 的图象交于点 $P (n ， - 4)$ ，则关于 $x$ 的不等式 $k x + b < - x - 2$ 的解集为.

查看试题解析
14. 某品牌服装的进价为100元，出售时标价为120元，为促销，商店决定降价销售，但是要保证利润不低5%，那么商店最多降价元出售．

查看试题解析
15. 如图，在 $△ A B C$ 中， $A B = 8$ ，将 $△ A B C$ 绕点 $B$ 按逆时针方向旋转 $30 °$ 后得到 $△ A_{1} B C_{1}$ ，则阴影部分面积为．

查看试题解析

三、解答题

16. 下面是小颖同学解一元一次不等式 $\frac{2 x + 1}{3} - \frac{x + 2}{6} < 2$ 的解答过程，请认真阅读并完成相应任务．
解：去分母，得 $2 (2 x + 1) - (x + 2) < 12$ ，           第一步
去括号，得 $4 x + 2 - x + 2 < 12$ ，              第二步
移项、合并同类项，得 $3 x < 8$ ，              第三步
两边都除以3，得 $x < \frac{8}{3}$ ．                第四步

(1)、任务一：填空：
①以上运算步骤中，去分母的依据是；
②第步开始出现错误，这一步错误的原因是；

(2)、任务二：请直接写出正确的计算结果；

(3)、任务三：除纠正上述错误外，请你根据平时的学习经验，解一元一次不等式时，还需要注意的事项给其他同学提一条建议．

查看试题解析
17. 解下列不等式组，并在数轴上表示出不等式组的解集：

(1)、 ${\begin{cases} 1 - 3 x > - 5 \\ x - 1 \leq - 2 (x + 2) \end{cases}$

(2)、 ${\begin{array}{l} 4 (x + 1) \leq 7 x + 13 \\ x - 4 < \frac{x - 8}{3} \end{array}$

查看试题解析
18. 如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，坐标分别为A（2，2），B（1，0），C（3，1）．
（ 1 ）画出△ABC关于y轴对称的△ $A_{1}$ $B_{1}$ $C_{1}$ ；
（ 2 ）画出将△ABC绕原点O顺时针旋转90°所得的△ $A_{2}$ $B_{2}$ $C_{2}$ ；
（ 3 ）△ $A_{1}$ $B_{1}$ $C_{1}$ 与△ $A_{2}$ $B_{2}$ $C_{2}$ ₂成中心对称图形吗？若成中心对称图形，直接写出对称中心的坐标．

查看试题解析
19. 为了进一步丰富校园活动，学校准备购买一批足球和篮球，已知购买7个足球和5个篮球的费用相同；购买40个足球和20个篮球共需3400元.

(1)、求每个足球和篮球各多少元？

(2)、如果学校计划购买足球和篮球共80个，总费用不超过4800元，那么最多能买多少个篮球？

查看试题解析
20. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ D A C$ 是 $△ A B C$ 的一个外角．
实践与操作：
根据要求尺规作图，并在图中标明相应字母（保留作图痕迹，不写作法）．
( 1 )作 $∠ D A C$ 的平分线AM；
( 2 )作线段AC的垂直平分线，与AM交于点F，与BC边交于点E，连接AE、CF．
( 3 )若 $A E = 5$ ， $E F = 8$ ，求AB的长．

查看试题解析
21. 全球棉花看中国，中国棉花看新疆．新疆棉花品质优，产量大，甲、乙两个供货商提供的棉花品质一样，报价均为15000元/吨，某纺织厂计划购进x吨（x＞10）新疆棉花，两个供货商分别给出如下优惠方案：
甲：一次性购进10吨以上时，每吨的售价优惠5%；
乙：一次性购进10吨以上时，10吨及10吨以内的部分按报价付费，超过10吨的部分，每吨的售价优惠10%（不计其他费用）；
怎么购买更实惠？

查看试题解析
22. 已知△ABC和△ADE都是等腰三角形，且AB＝AC，AD＝AE，∠DAE＝∠BAC．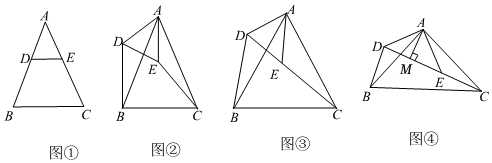

(1)、[初步感知]如图①，当点D、E分别落在边AB、AC上时，那么DBEC．（填＜、＞或＝）

(2)、[发现证明]如图②，将图①中的△ADE的绕点A旋转，当点D在△ABC外部，点E在△ABC内部时，求证：DB＝EC；

(3)、[深入研究]如图③，如果△ABC和△ADE都是等边三角形，且点C、E、D在同一条直线上，则∠CDB的度数为；线段CE、BD之间的数量关系为；

(4)、[拓展应用]如图④，如果△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，点C、D、E在同一直线上，作AM⊥DE，若AB＝ $\sqrt{6}$ ， BD＝ $\sqrt{3}$ ，求AM的长．

查看试题解析
23. 综合与探究：
如图所示，已知 $△ A B C$ 中， $∠ B = 90 °$ ， $A B = 16 c m$ ， $A C = 20 c m$ ， P、Q是 $△ A B C$ 的边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒 $1 c m$ ，点Q从点B开始沿B→C→A方向运动，且速度为每秒 $2 c m$ ，它们同时出发，设出发的时间为 $t s$ ．
（备用图1）（备用图2）

(1)、求BC的长；

(2)、当t为何值时，点P在边AC的垂直平分线上？并求出此时CQ的值；

(3)、当点Q在边CA上运动时，是否存在t的值，使 $△ B C Q$ 为等腰三角形，若存在，请求出t的值；若不存在，请说明理由．

查看试题解析