山西省大同市阳高县2021-2022学年八年级下学期期中数学试题

试卷更新日期：2023-03-13 类型：期中考试

进入出卷网下载

一、单选题

1. 若 $\sqrt{2 x + 1}$ 有意义，则（）

A、 $x \geq - \frac{1}{2}$ B、 $x > - \frac{1}{2}$ C、 $x \neq \frac{1}{2}$ D、 $x \geq \frac{1}{2}$

查看试题解析
2. 下列运算结果正确的是（）

A、 $\sqrt{3} + \sqrt{3} = \sqrt{6}$ B、 $6 \div \sqrt{6} = \sqrt{6}$ C、 $\sqrt{(- 6)^{2}} = \sqrt{6}$ D、 $\sqrt{12} \times \frac{1}{2} = \sqrt{6}$

查看试题解析
3. 下列∠A：∠B：∠C：∠D的值中，能判定四边形ABCD是平行四边形的是（）

A、1：2：3：4 B、1：4：2：3 C、1：2：2：1 D、3：2：3：2

查看试题解析
4. 如图，在 $R t Δ A B C$ 中， $∠ A C B = 90 °$ ， D，E分别是AB，AC的中点，连接CD，过E作 $E F$ // $D C$ 的延长线于F，若四边形CDEF的周长是10cm，AC的长为4cm，则 $△ A B C$ 的周长是____cm．

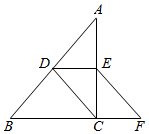A、14 B、15 C、16 D、17

查看试题解析
5. 2021年7月11日至18日，第十四届国际数学教育大会（ICME14）在上海举行．如图是ICME14的会标，包含了大量的中国数学元素——河图、洛书、弦图、八卦等，其中的“弦图”也是中国数学会的徽标．下列中国古代数学成就中，与“弦图”有关的是（）

A、天元术 B、正负术 C、勾股定理 D、杨辉三角

查看试题解析
6. 如图，平行四边形ABCD的对角线AC，BD相交于点O，下列结论错误的是（　　）

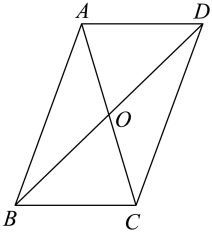A、AO＝CO B、AD∥BC C、AD＝BC D、∠DAC＝∠ACD

查看试题解析
7. 如图，数学课上老师给出了以下四个条件：a两组对边分别相等；b一组对边平行且相等；c一组邻边相等；d一个角是直角．有三位同学给出了不同的组合方式：①a，c，d；②b，c，d；③a，b，c．你认为能得到正方形的是（）

A、仅① B、仅③ C、①② D、②③

查看试题解析
8. 如图，某超市为了吸引顾客，在超市门口离地高4.5m的墙上，装有一个由传感器控制的门铃A，如①图所示，人只要移至该门铃5m及5m以内时，门铃就会自动发出语音“欢迎光临”.如②图所示，一个身高1.5m的学生走到D处，门铃恰好自动响起，则BD的长为（）

A、3米 B、4米 C、5米 D、7米

查看试题解析
9. 如图，在菱形ABCD中，对角线AC与BD相交于点O，且AC＝12，BD＝16，则菱形的高AE为（）

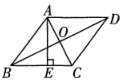A、9.6 B、4.8 C、10 D、5

查看试题解析
10. 如图，矩形 $A B C D$ 中， $A B = 3 ， A D = 1 ， A B$ 在数轴上，若以点A为圆心，对角线 $A C$ 的长为半径作到交数轴的正半轴于M，则点M，在数轴上表示的数为（）

A、2 B、 $\sqrt{5} - 1$ C、 $\sqrt{10} - 1$ D、 $\sqrt{5}$

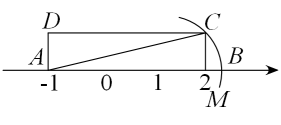查看试题解析

二、填空题

11. 化简： $\sqrt{14} \div \sqrt{2} =$ ．

查看试题解析
12. 若 $\sqrt{84 n}$ 是整数，则正整数n的最小值是．

查看试题解析
13. 数学活动课上，同学们利用升旗的绳子测量旗杆的高度．将绳子紧靠旗杆拉直，测得绳子比旗杆多0.5m（如图1）；然后拉着绳子的底端往后拉，当绳子拉直时，测得绳子的末端到地面的距离CD为0.5m，到旗杆的距离CE为3.5m（如图2），若设旗杆高为xm，则x满足的方程为．

查看试题解析
14. 如图，在▱ABCD中，AB＝3，AD＝5，∠ABC的平分线交AD于E，交CD的延长线于点F，则DF＝．

查看试题解析
15. 如图，已知 $△ A B C$ 中， $∠ A C B = 90 °$ ， $B C = 6$ ， $A C = 8$ ，点D是AC边上的一个动点．将 $△ A B C$ 沿BD所在直线折叠，点C的对应点为点E．如图，若 $C D = 2$ ，则C，E两点之间的距离为．

查看试题解析

三、解答题

16. 计算：

(1)、 $\sqrt{18} - \sqrt{8} + \sqrt{\frac{1}{2}} \times \sqrt{50}$

(2)、 $\sqrt{15} \div \sqrt{5} + {(3 - \sqrt{3})}^{2}$

(3)、 $(\sqrt{5} - \sqrt{3}) (\sqrt{5} + \sqrt{3}) + 1$ ；

查看试题解析
17. 下面是王鑫同学进行实数运算的过程，认真阅读并完成相应的问题：
$\sqrt{\frac{9}{2}} - \sqrt{12} \times (\sqrt{24} + 3 \sqrt{\frac{2}{3}})$
$= \frac{\sqrt{9}}{\sqrt{2}} - \sqrt{12} \times (\sqrt{24} + 3 \sqrt{\frac{2}{3}})$ ……第一步
$= \frac{3 \sqrt{2}}{2} - 2 \sqrt{3} \times 2 \sqrt{6} + 2 \sqrt{3} \times 3 \sqrt{\frac{2}{3}}$ ……第二步
$= \frac{3 \sqrt{2}}{2} - 12 \sqrt{2} + 6 \sqrt{2}$ ……第三步
$= \frac{9 \sqrt{2}}{2}$ ……第四步
①以上化简步骤中第一步化简的依据是：；
②第步开始出现错误，请写出错误的原因；
③该运算正确结果应是．

查看试题解析
18. 交通警察通常根据刹车后车轮滑过的距离估计车辆行驶的速度．在某高速公路上，所用的经验公式是 $v^{2} = 256 (d f + 1)$ ，其中v表示车速（单位：千米/小时），d表示刹车后车轮滑过的距离（单位：米），f表示摩擦系数， $f = 1.25$ ，在这条高速公路调查一次交通事故中，测得 $d = 28$ 米，求肇事汽车的速度大约是多少？

查看试题解析
19. 如图，四边形ABCD是平行四边形，E，F是对角线AC的三等分点，连接BE，DF．证明BE=DF．

查看试题解析
20. 滑梯的示意图如图所示，左边是楼梯，右边是滑道，立柱 $B C$ ， $D E$ 垂直于地面 $A F$ ，滑道 $A C$ 的长度与点A到点E的距离相等，滑梯高 $B C = 1.5 m$ ，且 $B E = 0.5 m$ ，求滑道 $A C$ 的长度.

查看试题解析
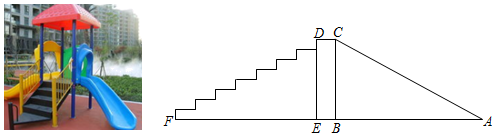
21. 如图，在矩形ABCD中，对角线BD的垂直平分线EF分别与AD，BC交于点E、F，与BD交于点O，连接BE，DF．

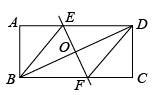(1)、求证：四边形BEDF是菱形；

(2)、若 $A B = 4$ ， $A D = 8$ ，求菱形BEDF的面积．

查看试题解析
22. 阅读与思考，阅读下列材料，完成相应的任务．
欧几里德数
一般地，给定单位长度1，一个数如果可以借助图形构造出来，我们就称这个数为欧几里德数．例如，如图1所示的方格图中，设每个小正方形的边长为单位1．借助方格图，可以构造出线段AB，CD，EF分别表示正整数2，3，4，也可以构造出线段MN表示正分数 $\frac{1}{2}$ ．事实上，所有的正有理数都是欧几里德数．
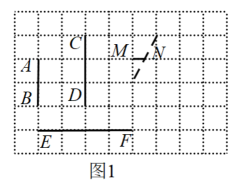
任务：如图2，图3，图4所示的方格图中，每个小正方形的边长均为单位长度1．

(1)、请在图2中用两种方法构造线段表示正整数5（该线段的端点均为格点）；

(2)、小彬由材料中的结论出发展开联想，经过探究，发现正无理数 $\sqrt{2}$ ， $\sqrt{3}$ 也是欧几里德数，可分别用图3中两个三角形的边XY，PQ表示，其思考与作图方法如下：
$\sqrt{2} = \sqrt{1^{2} + 1^{2}}$ ，取网格中 $M X = M Y = 1$ ，且 $∠ X M Y = 90 °$ ，连接XY，则 $X Y = \sqrt{1^{2} + 1^{2}} = \sqrt{2}$ ．
$\sqrt{3} = \sqrt{2^{2} - 1^{2}}$ ，取网格中线段 $O N = 2$ ， $O Q = 1$ ，以点O为圆心，ON长为半径作弧交网格线于点P，连接OP，且 $P Q ⊥ O Q$ ，则 $P Q = \sqrt{3}$ ．
在图4中借助网格和尺规，用两种方法构造三角形，使三角形的一边表示欧几里德数 $2 \sqrt{2}$ （保留作图痕迹，不写作法）．

查看试题解析
23. 如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC ．设MN交∠ACB的平分线于点E ，交∠ACB的外角平分线于点F ．

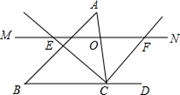(1)、求证：OE=OF；

(2)、当点O在边AC上运动到什么位置时，四边形AECF是矩形？并说明理由．

(3)、当点O运动到何处，且△ABC满足什么条件时，四边形AECF是正方形？

查看试题解析