山西省大同市2021-2022学年八年级下学期期中数学试题
试卷更新日期:2023-03-13 类型:期中考试
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 下列二次根式是最简二次根式的是( )A、 B、 C、 D、3. 根据我国古代一部数学著作记载,在约公元前1100年,人们就已经知道如果勾是三、股是四,那么弦是五,这本数学著作是( )A、《周髀算经》 B、《九章算术》 C、《几何原本》 D、《海岛算经》4. 在▱ABCD中,若∠B=70°,则∠D=( )A、35° B、70° C、110° D、130°5. 矩形具有而平行四边形不一定具有的性质是( )A、对边相等 B、对角相等 C、对角线相等 D、对角线互相平分6. 下列各组数据中的三个数,可作为三边长构成直角三角形的是( )A、1、2、3 B、 C、 D、7. 如图,在▱ABCD中,对角线AC,BD相交于点O,添加下列条件不能判定▱ABCD是菱形的只有( )
 A、AC⊥BD B、AB=BC C、AC=BD D、∠1=∠28. 如图,为了测量池塘边A、B两地之间的距离,在的同侧取一点C,连接并延长至点D,使得 , 连接并延长至点E,使得 . 若 , 则的长为( )
A、AC⊥BD B、AB=BC C、AC=BD D、∠1=∠28. 如图,为了测量池塘边A、B两地之间的距离,在的同侧取一点C,连接并延长至点D,使得 , 连接并延长至点E,使得 . 若 , 则的长为( ) A、12m B、10m C、9m D、8m9. 如图,在中, , D为的中点,若 , 则的度数为( )
A、12m B、10m C、9m D、8m9. 如图,在中, , D为的中点,若 , 则的度数为( ) A、55° B、35° C、45° D、30°10. 如图,将两条宽度都为3的纸条重叠在一起,使 , 则四边形的面积为( )
A、55° B、35° C、45° D、30°10. 如图,将两条宽度都为3的纸条重叠在一起,使 , 则四边形的面积为( )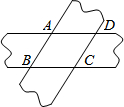 A、9 B、 C、 D、6
A、9 B、 C、 D、6二、填空题
-
11. 二次根式 中, 的取值范围是.12. 如图,在平面直角坐标中,有两点 , , 则A,B两点间的距离是
 13. 《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,中,∠ACB=90°,AC+AB=10,BC=3,求AC的长,如果设AC=x,则可列方程为(方程不用化简).
13. 《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,中,∠ACB=90°,AC+AB=10,BC=3,求AC的长,如果设AC=x,则可列方程为(方程不用化简). 14. 写出命题“如果两个实数都是正数,那么它们的积是正数”的逆命题是15. 如图,正方形的边长为4,E,F,H分别是边 , , 上的一点,将正方形沿折叠,使点D恰好落在边的中点E处,点A的对应点为点P,则折痕的长为 .
14. 写出命题“如果两个实数都是正数,那么它们的积是正数”的逆命题是15. 如图,正方形的边长为4,E,F,H分别是边 , , 上的一点,将正方形沿折叠,使点D恰好落在边的中点E处,点A的对应点为点P,则折痕的长为 .
三、解答题
-
16. 计算:(1)、(2)、17. 如图,四边形和都是平行四边形.求证:四边形是平行四边形.
 18. 已知a,b分别是的整数部分和小数部分.(1)、分别写出a,b的值;(2)、求的值.19. 现有5个边长为1的正方形,排列形式如图①,请把它们分割后拼接成一个新的正方形.要求:在图①中画出分割线并在图②正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.
18. 已知a,b分别是的整数部分和小数部分.(1)、分别写出a,b的值;(2)、求的值.19. 现有5个边长为1的正方形,排列形式如图①,请把它们分割后拼接成一个新的正方形.要求:在图①中画出分割线并在图②正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.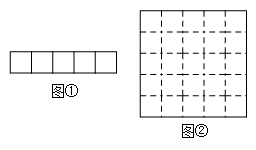 20. 数学活动课上,老师要求同学们制作一个长方体礼品盒,盒子的下底面的面积为 , 长、宽、高的比为 .
20. 数学活动课上,老师要求同学们制作一个长方体礼品盒,盒子的下底面的面积为 , 长、宽、高的比为 . (1)、计算出这个长方体的长、宽、高分别是多少?(2)、把这个长方体的高的值在数轴上表示出来;
(1)、计算出这个长方体的长、宽、高分别是多少?(2)、把这个长方体的高的值在数轴上表示出来; (3)、一支长为6.5cm的钢笔要放入这个长方体盒内,能放进去吗?试通过计算说明你的结论.(提示:长方体的高垂直于底面的任何一条直线)21. 阅读下列材料并完成相应的任务
(3)、一支长为6.5cm的钢笔要放入这个长方体盒内,能放进去吗?试通过计算说明你的结论.(提示:长方体的高垂直于底面的任何一条直线)21. 阅读下列材料并完成相应的任务等面积法是一种常用的、重要的数学解题方法.它是利用“同一个图形的面积相等”、“分割图形后各部分的面积之和等于原图形的面积”、“同底等高或等底同高的两个三角形面积相等”等性质解决有关数学问题.在解题中,灵活运用等面积法解决相关问题,可以使解题思路清晰,解题过程简便快捷.
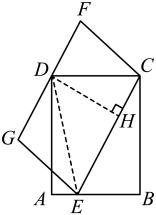
如图,矩形的边上有一动点E,以为边作 , 且边过矩形的顶点D,在点E从点A移动到点B的过程中,的面积如何变化?
小亮的观点:过点D作于点H,连接 . 与的乘积始终等于 , 所以的面积不变.
小明的观点:在点E的运动过程中,的长度在变化,而与两条平行线间的距离不变,所以的面积变化.
任务:你认为小亮和小明谁的观点正确?正确的写出完整的证明过程.
 22. 综合与实践
22. 综合与实践问题情境:
数学活动课上,老师和同学们一起以“矩形纸片的折叠”为主题开展数学活动.
动手操作
操作1:如图1,将矩形纸片沿着对角线折叠,顶点C落在点E处,交于点F.
操作2:如图2,在操作1的基础上,过点D作 , 交于点G,连接交于点O.
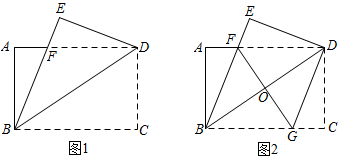 (1)、在图1中,求证是等腰三角形;(2)、在图2中,判断四边形的形状,并说明理由;(3)、在图2中,若 , , 直接写出的长.23. 综合与探究
(1)、在图1中,求证是等腰三角形;(2)、在图2中,判断四边形的形状,并说明理由;(3)、在图2中,若 , , 直接写出的长.23. 综合与探究如图,中,点A,B,C在坐标轴上,点C的坐标是 , , , 点M,N分别以A,C为起点,以的速度沿 , 方向同时运动,设点M,N的运动时间为t秒 .
 (1)、求点B的坐标.(2)、连接 , , 当t为何值时,四边形为菱形.(3)、若点P是x轴上一动点(点P不与B,C重合),点Q是y轴上一动点,试判断是否存在这样的点P,使得以点C,D,P,Q为顶点的四边形是平行四边形.若存在,请直接写出点P的坐标,若不存在,请说明理由.
(1)、求点B的坐标.(2)、连接 , , 当t为何值时,四边形为菱形.(3)、若点P是x轴上一动点(点P不与B,C重合),点Q是y轴上一动点,试判断是否存在这样的点P,使得以点C,D,P,Q为顶点的四边形是平行四边形.若存在,请直接写出点P的坐标,若不存在,请说明理由.