河北省保定市阜平县2021-2022学年八年级下学期期中数学试题
试卷更新日期:2023-03-13 类型:期中考试
一、单选题
-
1. 下列各式中,属于最简二次根式的是( )A、 B、 C、 D、2. 在 中,若 ,则( )A、 B、 C、 D、不能确定3. 墨迹覆盖了等式“”中的运算符号,则覆盖的是( )A、+ B、- C、× D、÷4. 如图,ABCD的对角线AC,BD相交于点O,则下列结论一定正确的是( )
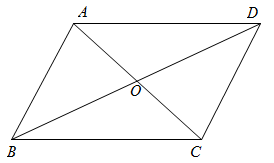 A、OA=OC B、AB=AC C、∠ABD=∠CBD D、AC⊥BD5. 与结果相同的是( )A、 B、 C、 D、6. 如图,在中,是斜边上的中线, , 则的度数是( )
A、OA=OC B、AB=AC C、∠ABD=∠CBD D、AC⊥BD5. 与结果相同的是( )A、 B、 C、 D、6. 如图,在中,是斜边上的中线, , 则的度数是( )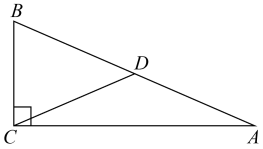 A、40° B、50° C、60° D、70°7. 化简的结果为( )A、 B、 C、 D、8. 如图,在离地面高3m处引拉线固定电线杆,拉线AC=BC,且和地面成60°,则拉线BC的长是( )
A、40° B、50° C、60° D、70°7. 化简的结果为( )A、 B、 C、 D、8. 如图,在离地面高3m处引拉线固定电线杆,拉线AC=BC,且和地面成60°,则拉线BC的长是( )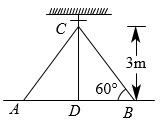 A、6m B、 C、 D、9. 如果最简二次根式与能够合并,那么a的值为( )A、1 B、2 C、4 D、1010. 两张全等的矩形纸片ABCD,AECF按如图所示的方式交叉叠放,AB=AF,AE=BC.AE与BC交于点G,AD与CF交于点H,且∠AGB=30°,AB=2,则四边形AGCH的周长为( )
A、6m B、 C、 D、9. 如果最简二次根式与能够合并,那么a的值为( )A、1 B、2 C、4 D、1010. 两张全等的矩形纸片ABCD,AECF按如图所示的方式交叉叠放,AB=AF,AE=BC.AE与BC交于点G,AD与CF交于点H,且∠AGB=30°,AB=2,则四边形AGCH的周长为( )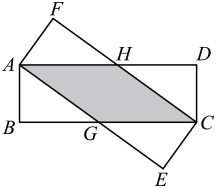 A、4 B、8 C、 D、1611. 如图,矩形中,在数轴上,若以点A为圆心,对角线的长为半径作到交数轴的正半轴于M,则点M,在数轴上表示的数为( )
A、4 B、8 C、 D、1611. 如图,矩形中,在数轴上,若以点A为圆心,对角线的长为半径作到交数轴的正半轴于M,则点M,在数轴上表示的数为( )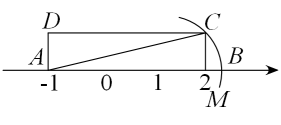 A、2 B、 C、 D、12. 如图,在中,D,E,F分别是边 , , 的中点,连接 , , , , , 则下列说法正确的是( )
A、2 B、 C、 D、12. 如图,在中,D,E,F分别是边 , , 的中点,连接 , , , , , 则下列说法正确的是( )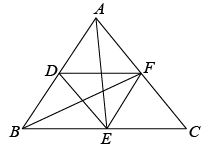 A、是的中位线 B、是的中位线 C、是的中位线 D、DF是的中位线13. 如图,▱ABCD的对角线AC与BD相交于点O,AB⊥AC.若AB=4,AC=6,则BD的长是( )
A、是的中位线 B、是的中位线 C、是的中位线 D、DF是的中位线13. 如图,▱ABCD的对角线AC与BD相交于点O,AB⊥AC.若AB=4,AC=6,则BD的长是( ) A、8 B、9 C、10 D、1114. 如图所示的是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五块正方形纸片,面积分别是1,2,3,4,5,选取其中三块,按图中的方式组成图案,则选取的三块纸片不可能的是( )
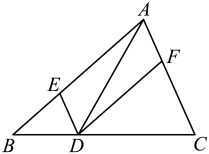
A、8 B、9 C、10 D、1114. 如图所示的是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五块正方形纸片,面积分别是1,2,3,4,5,选取其中三块,按图中的方式组成图案,则选取的三块纸片不可能的是( )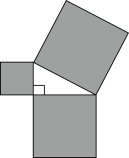 A、3,4,5 B、1,3,4 C、2,3,5 D、1,4,515. 如图,在中,点D、E、F分别在边上,且 . 下列四种说法,其中正确的有( )个
A、3,4,5 B、1,3,4 C、2,3,5 D、1,4,515. 如图,在中,点D、E、F分别在边上,且 . 下列四种说法,其中正确的有( )个①四边形是平行四边形:
②如果 , 则四边形是矩形:
③如果平分 , 则四边形是菱形:
④如果且 , 则四边形是菱形,
 A、1 B、2 C、3 D、416. 如图是放在地面上的一个长方体盒子,其中AB=18cm,BC=12cm,BF=10cm,点M在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为( )
A、1 B、2 C、3 D、416. 如图是放在地面上的一个长方体盒子,其中AB=18cm,BC=12cm,BF=10cm,点M在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为( )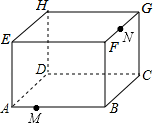 A、20cm B、2cm C、(12+2)cm D、18cm
A、20cm B、2cm C、(12+2)cm D、18cm二、填空题
-
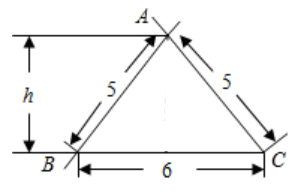
17. 若有意义,则x= , 此时 .18. 已知一个三角形工件尺寸(单位: )如图所示,则高h是 ,它的面积是 .
 19. 如图,在矩形中, , 相交于点O,过点B作交于点F,交于点M,过点D作交于点E,交于点N,连接 , .
19. 如图,在矩形中, , 相交于点O,过点B作交于点F,交于点M,过点D作交于点E,交于点N,连接 , .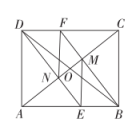 (1)、若 , 则;(2)、当时,四边形是菱形.
(1)、若 , 则;(2)、当时,四边形是菱形.三、解答题
-
20. 求代数式的值,其中 , 如图所示的是小亮和小芳的解答过程.
 (1)、的解法是错误的.(2)、求代数式的值,其中 .21. 如图,在笔直的公路AB旁有一座山,为方便运输货物现要从公路AB上的D处开凿隧道通一条公路到C处,已知点C与公路上的停靠站A的距离为3km,与公路上另一停靠站B的距离为4km,且AC⊥BC,CD⊥AB.
(1)、的解法是错误的.(2)、求代数式的值,其中 .21. 如图,在笔直的公路AB旁有一座山,为方便运输货物现要从公路AB上的D处开凿隧道通一条公路到C处,已知点C与公路上的停靠站A的距离为3km,与公路上另一停靠站B的距离为4km,且AC⊥BC,CD⊥AB.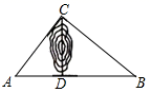 (1)、求修建的公路CD的长;(2)、若公路CD建成后,一辆货车由C处途经D处到达B处的总路程是多少km?22. 如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,过点E作EF∥CD交BC的延长线于点F , 连接CD .
(1)、求修建的公路CD的长;(2)、若公路CD建成后,一辆货车由C处途经D处到达B处的总路程是多少km?22. 如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,过点E作EF∥CD交BC的延长线于点F , 连接CD .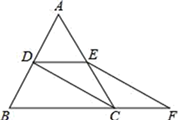 (1)、求证:DE=CF;(2)、求EF的长.23. 如图,P是菱形ABCD的对角线AC上一点,PE⊥AB于点E,PF⊥AD于点F.
(1)、求证:DE=CF;(2)、求EF的长.23. 如图,P是菱形ABCD的对角线AC上一点,PE⊥AB于点E,PF⊥AD于点F.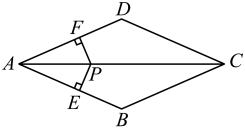 (1)、若∠BAD=60°,PE=1,求AE的长.(2)、若∠BAD=90°,判断四边形AEPF的形状,并说明理由.24. 某海上有一小岛,为了测量小岛两端A,B的距离,测量人员设计了一种测量方法,如图,已知B是CD的中点,E是BA延长线上的一点,且∠CED=90°,测得AE=16.6海里,DE=60海里,CE=80海里.
(1)、若∠BAD=60°,PE=1,求AE的长.(2)、若∠BAD=90°,判断四边形AEPF的形状,并说明理由.24. 某海上有一小岛,为了测量小岛两端A,B的距离,测量人员设计了一种测量方法,如图,已知B是CD的中点,E是BA延长线上的一点,且∠CED=90°,测得AE=16.6海里,DE=60海里,CE=80海里.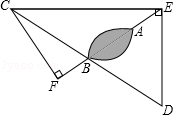 (1)、求小岛两端A,B的距离.(2)、过点C作CF⊥AB交AB的延长线于点F,求值.25. 菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为菱形或矩形的“接近度”.
(1)、求小岛两端A,B的距离.(2)、过点C作CF⊥AB交AB的延长线于点F,求值.25. 菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为菱形或矩形的“接近度”.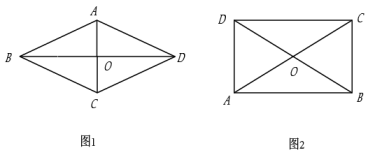 (1)、如图1,已知菱形ABCD的边长为2,设菱形ABCD的对角线AC,BD的长分别为m,n.若我们将菱形的“接近度”定义为(即“接近度”=),于是越小,菱形就越接近正方形.
(1)、如图1,已知菱形ABCD的边长为2,设菱形ABCD的对角线AC,BD的长分别为m,n.若我们将菱形的“接近度”定义为(即“接近度”=),于是越小,菱形就越接近正方形.①若菱形的“接近度”= , 菱形就是正方形;
②若菱形的一个内角为60°,则“接近度”= .
(2)、如图2,已知矩形ABCD的对角线AC,BD相交于点O,设AB,BC的长分别为m,n,我们将矩形的“接近度”定义为(即“接近度”=).①若矩形的“接近度”= ▲ , 矩形就是正方形;
②若∠AOD=45°,求矩形的“接近度”.
26. 在综合与实践课上,老师组织同学们以“矩形纸片的折叠”为主题开展数学活动.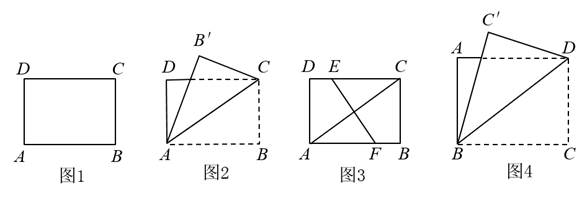 (1)、奋进小组用图1中的矩形纸片 , 按照如图2所示的方式,将矩形纸片沿对角线折叠,使点B落在点处,则与重合部分的三角形的形状是 .(2)、勤学小组将图2中的纸片展平,再次折叠(如图3),使点A与点C重合,折痕为 , 然后展平,则以点A,F,C,E为顶点的四边形是什么特殊四边形?请说明理由.(3)、创新小组用图4中的矩形纸片进行操作,其中 , , 先沿对角线对折,点C落在点的位置,交于点G,则的长为 .
(1)、奋进小组用图1中的矩形纸片 , 按照如图2所示的方式,将矩形纸片沿对角线折叠,使点B落在点处,则与重合部分的三角形的形状是 .(2)、勤学小组将图2中的纸片展平,再次折叠(如图3),使点A与点C重合,折痕为 , 然后展平,则以点A,F,C,E为顶点的四边形是什么特殊四边形?请说明理由.(3)、创新小组用图4中的矩形纸片进行操作,其中 , , 先沿对角线对折,点C落在点的位置,交于点G,则的长为 .