(华师大版)2022-2023学年八年级数学下册18.2 平行四边形的判定 同步测试
试卷更新日期:2023-03-13 类型:同步测试
一、单选题
-
1. 对于命题:一组对边平行且相等的四边形是平行四边形,小明的证明过程( )
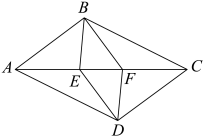
已知:如图,在四边形中,且
求证:四边形是平行四边形.
证明:连接 ,
在和中,
∵ , ∴
∵ ,
∴
∴
∴四边形是平行四边形
 A、已经严谨,不用补充 B、应补充“” C、应补充“” D、应补充“”2. 如图,点E、F分别是▱ABCD边AD、BC的中点,G、H是对角线BD上的两点,且BG=DH.则下列结论中错误的是( )
A、已经严谨,不用补充 B、应补充“” C、应补充“” D、应补充“”2. 如图,点E、F分别是▱ABCD边AD、BC的中点,G、H是对角线BD上的两点,且BG=DH.则下列结论中错误的是( ) A、 B、四边形EGFH是平行四边形 C、 D、3. 如图,在四边形ABCD中, , , 对角线AC,BD交于点O,AC平分 , 过点C作交AB的延长线与点E,连接OE.
A、 B、四边形EGFH是平行四边形 C、 D、3. 如图,在四边形ABCD中, , , 对角线AC,BD交于点O,AC平分 , 过点C作交AB的延长线与点E,连接OE.嘉嘉说:“四边形ABCD是菱形.”
琪琪说:“ . ”
对于他俩的说法,正确的是( )
 A、嘉嘉正确,琪琪错误 B、嘉嘉错误,琪琪正确 C、他俩都正确 D、他俩都错误4. 如图四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( )
A、嘉嘉正确,琪琪错误 B、嘉嘉错误,琪琪正确 C、他俩都正确 D、他俩都错误4. 如图四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( ) A、AB∥CD,∠DAC=∠BCA B、AB=CD,∠ABO=∠CDO C、AC=2AO,BD=2BO D、AO=BO,CO=DO5. 如图,已知四边形 , 下列说法中正确的是( )
A、AB∥CD,∠DAC=∠BCA B、AB=CD,∠ABO=∠CDO C、AC=2AO,BD=2BO D、AO=BO,CO=DO5. 如图,已知四边形 , 下列说法中正确的是( ) A、若 , , 则四边形是矩形 B、若 , , 则四边形是菱形 C、若 , 则四边形是正方形 D、若 , , 则四边形是平行四边形6. 如图,四边形ABCD中,AB=CD.添加下列一个条件后能使四边形ABCD成为平行四边形的是( )
A、若 , , 则四边形是矩形 B、若 , , 则四边形是菱形 C、若 , 则四边形是正方形 D、若 , , 则四边形是平行四边形6. 如图,四边形ABCD中,AB=CD.添加下列一个条件后能使四边形ABCD成为平行四边形的是( ) A、AB//CD B、AD//BC C、AB=BC D、AB=AC7. 如图,在四边形ABCD中,ABCD,要使四边形ABCD是平行四边形,下列添加的条件错误的是( )
A、AB//CD B、AD//BC C、AB=BC D、AB=AC7. 如图,在四边形ABCD中,ABCD,要使四边形ABCD是平行四边形,下列添加的条件错误的是( ) A、AB=CD B、BC=AD C、∠A=∠C D、8. 如图,在一束平行光线中插入一张对边平行的纸板,如果光线与纸板右下方所成的 , 则光线与纸板左上方所成的的度数是( )
A、AB=CD B、BC=AD C、∠A=∠C D、8. 如图,在一束平行光线中插入一张对边平行的纸板,如果光线与纸板右下方所成的 , 则光线与纸板左上方所成的的度数是( ) A、 B、 C、 D、9. 如图所示,在平行四边形ABCD中,AB=3.5cm,BC=5cm,AE平分∠BAD,CF∥AE,则AF的长度是( )
A、 B、 C、 D、9. 如图所示,在平行四边形ABCD中,AB=3.5cm,BC=5cm,AE平分∠BAD,CF∥AE,则AF的长度是( )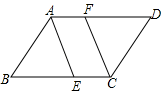 A、1.5cm B、2.5cm C、3.5cm D、0.5cm10. 如图,平行四边形中, , 是对角线上的两点,如果添加一个条件使四边形是平行四边形,则添加的条件不能是( )
A、1.5cm B、2.5cm C、3.5cm D、0.5cm10. 如图,平行四边形中, , 是对角线上的两点,如果添加一个条件使四边形是平行四边形,则添加的条件不能是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 在平面直角坐标系中,已知A、B、C、D四点的坐标依次为(0,0)、(6,0)、(8,6)、(2,6),若一次函数y=mx-6m的图象将四边形ABCD的面积分成1:3两部分,则m的值为 .12. 已知:如图,线段AB=6cm,点P是线段AB上的动点,分别以AP、BP为边在AB作等边APC、等边BPD,连接CD,点M是CD的中点,当点P从点A运动到点B时,点M经过的路径的长是cm.
 13. 如图,在ABC中, , , AD平分交BC于点D,P为直线AB上一动点.连接DP,以DP、DB为邻边构造平行四边形DPQB,连接CQ,若 . 则CQ的最小值为 .
13. 如图,在ABC中, , , AD平分交BC于点D,P为直线AB上一动点.连接DP,以DP、DB为邻边构造平行四边形DPQB,连接CQ,若 . 则CQ的最小值为 . 14. 如图,在梯形ABCD中, , E为BC中点, , , 点P以每秒3个单位长度的速度从点B出发向点C运动,同时点Q以每秒1个单位长度的速度从点D出发向点A运动,则经过秒后,以点A,E,P,Q为顶点的四边形是平行四边形.
14. 如图,在梯形ABCD中, , E为BC中点, , , 点P以每秒3个单位长度的速度从点B出发向点C运动,同时点Q以每秒1个单位长度的速度从点D出发向点A运动,则经过秒后,以点A,E,P,Q为顶点的四边形是平行四边形. 15. 如图,在平面直角坐标系中,函数的图象分别交x轴,y轴于A,B两点,过点A的直线交y轴正半轴于点M,且 . 在平面直角坐标系内存在点C,使得以A,B,M,C为顶点的四边形是平行四边形,则点C的坐标为 .
15. 如图,在平面直角坐标系中,函数的图象分别交x轴,y轴于A,B两点,过点A的直线交y轴正半轴于点M,且 . 在平面直角坐标系内存在点C,使得以A,B,M,C为顶点的四边形是平行四边形,则点C的坐标为 .
三、解答题
-
16. 如图,在中, , 、分别是、的中点,试判断四边形的形状,并证明之.
 17. 如图,点P,Q是对角线上的两个点,且 , 顺次连接 , , , .
17. 如图,点P,Q是对角线上的两个点,且 , 顺次连接 , , , .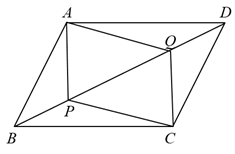
求证:四边形是平行四边形.
18. 如图,在中,点O是的中点,连接并延长交的延长线于点E,连接 , . 求证:四边形是平行四边形.
四、综合题
-
19. 如图,在平面直角坐标系中,直线y=-x+8分别交两坐标轴于点A、B,直线CD与直线AB交于点C,与x轴交于点D.点C的横坐标为4,点D在线段OA上,且AD=7.

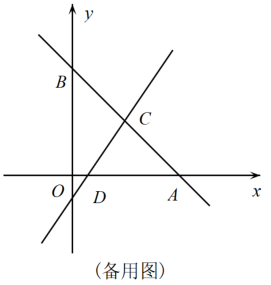
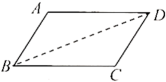
 (1)、C、D两点的坐标分别为;(2)、求直线CD的函数解析式;(3)、在坐标平面内是否存在这样的点F,使以A、C、D、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.20. 在四边形中,、交于点 , , .
(1)、C、D两点的坐标分别为;(2)、求直线CD的函数解析式;(3)、在坐标平面内是否存在这样的点F,使以A、C、D、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.20. 在四边形中,、交于点 , , . (1)、证明:四边形是平行四边形;(2)、过点作交于点 , 连接 . 若 , 求的度数.
(1)、证明:四边形是平行四边形;(2)、过点作交于点 , 连接 . 若 , 求的度数.