(华师大版)2022-2023学年八年级数学下册18.1 平行四边形的性质 同步测试
试卷更新日期:2023-03-13 类型:同步测试
一、单选题
-
1. 在平行四边形ABCD中,如果 , 那么的度数是( )A、 B、 C、 D、2. 如图,平行四边形ABCD的对角线AC与BD相交于点O,AB⊥AC.若AC=6,BD=10,则AB的长是( )
 A、3 B、4 C、5 D、63. 如图,在平行四边形中,若 , 则的度数为( )
A、3 B、4 C、5 D、63. 如图,在平行四边形中,若 , 则的度数为( ) A、 B、 C、 D、4. 如图,在中,BE⊥CD,BF⊥AD,∠EBF=45°,CE=3,DF=1,则AF=( )
A、 B、 C、 D、4. 如图,在中,BE⊥CD,BF⊥AD,∠EBF=45°,CE=3,DF=1,则AF=( ) A、 B、 C、 D、5. 如图,平行四边形ABCD的顶点A,B,C的坐标分别是(0, 2),(-1,-1)(2, -1),则顶点D的坐标是( )
A、 B、 C、 D、5. 如图,平行四边形ABCD的顶点A,B,C的坐标分别是(0, 2),(-1,-1)(2, -1),则顶点D的坐标是( ) A、(-3, 2) B、(3, -2) C、(3, 2) D、(2, 2)6. 如图,四边形ABCD是平行四边形,点B在线段BC的延长的,若∠DCE=130°,则∠A=( )
A、(-3, 2) B、(3, -2) C、(3, 2) D、(2, 2)6. 如图,四边形ABCD是平行四边形,点B在线段BC的延长的,若∠DCE=130°,则∠A=( ) A、40° B、50° C、130° D、都不对7. 平行四边形相邻两角中,其中一个角的度数与另一个角的度数之间的关系是( )A、 B、 C、 D、8. 平行四边形不一定具有的特征是( )A、两组对边分别平行 B、两组对角分别相等 C、对角线相等 D、内角和为360°9. 如图,四边形ABCD是平行四边形,以点A为圆心,AB的长为半径画弧,交AD于点F;分别以点B,F为圆心,大于的长为半径画弧,两弧相交于点G:连接AG并延长,交BC于点E.连接BF,若 , , 则AB的长为( )
A、40° B、50° C、130° D、都不对7. 平行四边形相邻两角中,其中一个角的度数与另一个角的度数之间的关系是( )A、 B、 C、 D、8. 平行四边形不一定具有的特征是( )A、两组对边分别平行 B、两组对角分别相等 C、对角线相等 D、内角和为360°9. 如图,四边形ABCD是平行四边形,以点A为圆心,AB的长为半径画弧,交AD于点F;分别以点B,F为圆心,大于的长为半径画弧,两弧相交于点G:连接AG并延长,交BC于点E.连接BF,若 , , 则AB的长为( )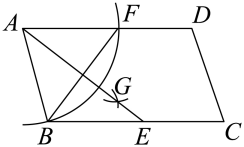 A、3 B、4 C、5 D、810. 若平行四边形中两内角的度数比为2∶3,则其中较小的内角是( ).A、36° B、45° C、60° D、72°
A、3 B、4 C、5 D、810. 若平行四边形中两内角的度数比为2∶3,则其中较小的内角是( ).A、36° B、45° C、60° D、72°二、填空题
-
11. 如图,在平行四边形中,对角线 , 相交于点O,在的延长线上取点E,使 , 连接交于点F,若 , 则 .
 12. 在平行四边形ABCD中,有两个内角的度数比为1:5,则平行四边形ABCD中较小内角的度数为 .13. 四边形ABCD是平行四边形,AB=8,∠BAD的平分线交直线BC于点E.若CE=2,则BC的长为 .14. 如图,在平行四边形ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB于点F,交DC的延长线于点G,则DE= .
12. 在平行四边形ABCD中,有两个内角的度数比为1:5,则平行四边形ABCD中较小内角的度数为 .13. 四边形ABCD是平行四边形,AB=8,∠BAD的平分线交直线BC于点E.若CE=2,则BC的长为 .14. 如图,在平行四边形ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB于点F,交DC的延长线于点G,则DE= . 15. 如图,在▱ABCD中,AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长 .
15. 如图,在▱ABCD中,AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长 .
三、解答题
-
16. 如图,在中,对角线AC和BD相交于点O, , , . 求OB的长.
 17. 如图,在ABCD中,BC=13,过点A作AE⊥DC于E,AE=12,CE=10.求AB的长;
17. 如图,在ABCD中,BC=13,过点A作AE⊥DC于E,AE=12,CE=10.求AB的长;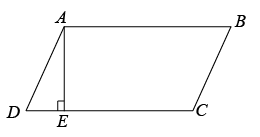 18. 如图,在▱中,对角线 , 交于点 , 若 , 求与的长.
18. 如图,在▱中,对角线 , 交于点 , 若 , 求与的长.
四、综合题
-
19. 如图,在平面直角坐标系中,过点 , 分别作x轴的垂线,垂足分别为A、B.
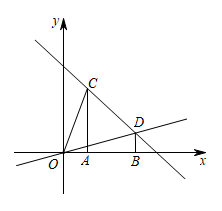 (1)、求直线CD和直线OD的解析式;(2)、点M为直线OD上的一个动点,过点M作x轴的垂线交x轴于点P,交直线CD于点N.
(1)、求直线CD和直线OD的解析式;(2)、点M为直线OD上的一个动点,过点M作x轴的垂线交x轴于点P,交直线CD于点N.①当PM为中位线时,求MN的长;
②是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由.
20. 如图,平行四边形ABCD中,AE平分交BC于E,DF平分交BC于F. (1)、求证:;(2)、若E为BC的三等分点(靠近C点), , , 求直线AB与CD之间的距离.21. 如图,在平面直角坐标系中,已知平行四边形的顶点为坐标原点,顶点在轴的正半轴上,在第一象限内, ,且 .
(1)、求证:;(2)、若E为BC的三等分点(靠近C点), , , 求直线AB与CD之间的距离.21. 如图,在平面直角坐标系中,已知平行四边形的顶点为坐标原点,顶点在轴的正半轴上,在第一象限内, ,且 . (1)、顶点的坐标为 ,顶点的坐标为;(2)、如图2,若直线过点 , 且把平行四边形的面积分成的两部分,求直线的函数解析式;(3)、如图3,设对角线交于点 ,在轴上,有一个长为1个单位长度的可以左右平移的线段 , 点在点的左侧,连接 , 则的最小值为 .
(1)、顶点的坐标为 ,顶点的坐标为;(2)、如图2,若直线过点 , 且把平行四边形的面积分成的两部分,求直线的函数解析式;(3)、如图3,设对角线交于点 ,在轴上,有一个长为1个单位长度的可以左右平移的线段 , 点在点的左侧,连接 , 则的最小值为 .


