鲁教版（五四学制）2022-2023学年七年级数学下册10.2 等腰三角形同步测试

试卷更新日期：2023-03-13 类型：同步测试

进入出卷网下载

一、单选题

1. 一个等腰三角形的三边长分别为3cm、acm、6cm，则它的周长是（）

A、12cm B、15cm C、12cm或15cm D、不能确定

查看试题解析
2. 如图，将△ABC绕点A顺时针旋转角100°，得到△ADE，若点E恰好在CB的延长线上，则∠BED的度数为（）

A、80° B、70° C、60° D、50°

查看试题解析
3. 已知等腰△ABC中，∠A＝50°，则∠B的度数为（）

A、50° B、65° C、50°或65° D、50°或65°或80°

查看试题解析
4. 如图，在△ABC中，DE垂直平分BC，若∠CDE＝64°，∠A＝28°，则∠ABD的度数为（）

A、100° B、128° C、108° D、98°

查看试题解析
5. 如图，在 $△ A B C$ 中， $A B = 4 ， B C = 6 ， ∠ B = 60 °$ ，将 $△ A B C$ 沿射线 $B C$ 方向平移得到 $△ A^{'} B^{'} C^{'}$ ，再将 $△ A^{'} B^{'} C^{'}$ 绕点 $A^{'}$ 逆时针旋转得到 $△ A^{'} C E$ ，此时点 $B^{'}$ 恰好与点C重合，点 $C^{'}$ 的对应点为E，则平移的距离和旋转角的度数分别为（）

A、2， $30 °$ B、4， $30 °$ C、2， $60 °$ D、4， $60 °$

查看试题解析
6. 如图，将 $△ A B C$ 绕点A按逆时针方向旋转100°得到 $A B^{^{'}} C^{^{'}}$ （点 $B$ 的对应点是点 $B^{'}$ ，点 $C$ 的对应点是点 $C^{'}$ ），连接 $B B'$ ，若 $A C^{'} ∥ B B^{'}$ ，则 $∠ C^{'} A B^{'}$ 的度数为（）

A、20° B、30° C、40° D、45°

查看试题解析
7. 如图，在等边三角形ABC中，BC=2，D是AB的中点，过点D作DF⊥AC于点F，过点F作EF⊥BC于点E，则BE的长为（）

A、1 B、 $\frac{3}{2}$ C、 $\frac{5}{4}$ D、 $\frac{4}{3}$

查看试题解析
8. 如图， $△ A B P$ 和 $△ C D P$ 是两个等边三角形， $△ A P D$ 是以 $A D$ 为斜边的等腰直角三角形，连接 $A C$ ， $B C$ ， $B D$ ，下列三个结论：① $△ A P C ≌ △ B P D$ ；② $△ A B D ≌ △ B C A$ ；③点 $P$ 在线段 $B C$ 的中垂线上；④ $∠ P B C = 15 °$ ；⑤ $A D ∥ B C$ ；⑥ $P C ⊥ A B$ ．其中正确的结论的个数是（）

A、3 B、4 C、5 D、6

查看试题解析
9. 已知等腰三角形的两边长分别为x、y，且满足 $| 2 x - y + 1 | + (x + y - 13)^{2} = 0$ ，则该等腰三角形的周长为（）

A、22或26 B、17 C、17或22 D、22

查看试题解析
10. 如图， $∠ B = ∠ C$ ， $A F ⊥ B C$ ，垂足为点F，点E在 $B C$ 上，且 $C D = C E$ ，若 $∠ A = 36 °$ ，则 $∠ D$ 的度数为（）

A、63° B、65° C、68° D、72°

查看试题解析

二、填空题

11. 等腰三角形的一条边长为4cm，另一条边长为6cm，则它的周长是．

查看试题解析
12. 等腰三角形的一个角是50°，则它的顶角的度数是．

查看试题解析
13. 如图，CD是△ABC的高，且CD平分∠ACB，∠BAC＝70°，∠CFE＝25°，则∠CEF＝°．

查看试题解析
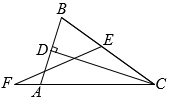14. 如果一个等腰三角形的两边长分别是5和7，则这个三角形的周长是.

查看试题解析
15. 如图，在△ABC中，AB＝AC，AD是BC边上的中线，在AD上取一点E，连接CE，使得AE＝CE，若∠ECD＝20°，则∠B＝°．

查看试题解析

三、解答题

16. 如图，在△ABC中，∠BAC＝105°，MP垂直平分AB，分别交AB、BC于点M、P，NQ垂直平分AC，分别交AC．BC于点N、Q，连接AP、AQ，求∠PAQ的度数．

查看试题解析
17. 如图，在△ABC中，AB＝AC，AD为BC边上的中线，∠CAD＝40°，EF为过点A的一条直线，且EF∥BC，求∠BAE的度数．

查看试题解析
18. 如图，在△ABC中，AB＝AC，点D、E在边BC上（点D在点E的左侧），请你再添加一个条件，使得∠BAD＝∠CAE，并说明理由．（不添加任何线条和字母）

查看试题解析

四、综合题

19. 分解因式x²－4y²－2x＋4y，细心观察这个式子就会发现，前两项符合平方差公式，后两项可提取公因式，前后两部分分别分解因式后会产生公因式，然后提取公因式就可以完成整个式子的分解因式，过程为：x²－4y²－2x＋4y＝(x＋2y)(x－2y)－2(x－2y)＝(x－2y)(x＋2y－2)．这种分解因式的方法叫分组分解法，利用这种方法解决下列问题：

(1)、分解因式： $a^{2} - 4 a - b^{2} + 4$ ；

(2)、若△ABC三边a、b、c满足a²－ab－ac＋bc＝0，试判断△ABC的形状．

查看试题解析
20. 已知：如图所示，在 $△ A B C$ 中， $B A = B C$ ， $∠ A B C = 48 °$ ， $C E ⊥ A B$ ，垂足为E，过点A作 $A D ∥ B C$ 交 $C E$ 延长线于点D．点P在线段 $D E$ 上，且 $∠ P A B = 30 °$ ，点M在线段 $C E$ 上，且 $A M = A P$ ，延长 $A M$ 交 $B C$ 于点Q，连接 $P Q$ ．

(1)、【观察分析】填空：
$∠ B C P$ 的度数是； $∠ P A D$ 的度数是； $∠ Q A C$ 的度数是；

(2)、【猜想说理】判断 $P E$ 与 $E M$ 的数量关系，并说明理由；

(3)、【拓展延伸】若点P关于 $B C$ 的对称点N恰好落在 $A Q$ 的延长线上，若 $P A = 3.2 c m$ ， $P Q = 5.6 c m$ ， $A Q = 6.6 c m$ ，请根据题意补全图形，并直接写出线段 $M N$ 的长及 $∠ Q P C$ 的度数．

查看试题解析
21. 如图，在Rt△ABC和Rt△EFD中，∠ABC＝∠EFD＝90°，AC＝ED，AC⊥ED，垂足为M，连接AE、CE．

(1)、△ABC与△EFD全等吗？为什么？

(2)、若∠AEF＝∠DEF，判断∠AEC与∠ACE的数量关系，并说明理由．

查看试题解析
22. 如图，直线EF分别交直线AB、CD于点E、F，EP平分∠AEF交CD于点P，点N是射线PC上一点，延长EP到点M，使得PM＝PN，连接MN．

(1)、若AB∥CD，∠EFD＝80°，求∠AEP的度数；

(2)、若∠PMN＝72.5°，∠AEF＝70°，判断直线AB与CD是否平行？并说明理由．

查看试题解析
23. 如图，在 $△ A B C$ 中，AD平分 $∠ B A C$ ，过点B作AD的垂线，垂足为点D， $D E ∥ A C$ ，交AB于点E， $C D ∥ A B$ ．

(1)、求证： $△ B D E$ 是等腰三角形；

(2)、求证： $C D = B E$ ．

查看试题解析

鲁教版（五四学制）2022-2023学年七年级数学下册10.2 等腰三角形 同步测试

一、单选题

二、填空题

三、解答题

四、综合题

鲁教版（五四学制）2022-2023学年七年级数学下册10.2 等腰三角形同步测试