(华师大版)2022-2023学年七年级数学下册10.3 旋转 同步测试
试卷更新日期:2023-03-13 类型:同步测试
一、单选题
-
1. 下列四张图形中,经过旋转之后不能得到的是( )A、
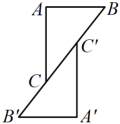 B、
B、 C、
C、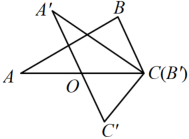 D、
D、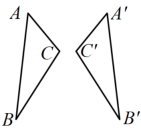 2. 如图所示,如图可以看作是一个菱形通过几次旋转得到的,每次可能旋转( )
2. 如图所示,如图可以看作是一个菱形通过几次旋转得到的,每次可能旋转( ) A、 B、 C、 D、3. 在如图所示的方格纸(1格长为1个单位长度)中,的顶点都在格点上,将绕点按顺时针方向旋转得到 , 使各顶点仍在格点上,则其旋转角的度数是( )
A、 B、 C、 D、3. 在如图所示的方格纸(1格长为1个单位长度)中,的顶点都在格点上,将绕点按顺时针方向旋转得到 , 使各顶点仍在格点上,则其旋转角的度数是( ) A、 B、 C、 D、4. 如图,将含有锐角的三角板绕的锐角顶点C逆时针旋转到 , 、相交于点F,连接 , 若 , 则旋转角的度数为( )
A、 B、 C、 D、4. 如图,将含有锐角的三角板绕的锐角顶点C逆时针旋转到 , 、相交于点F,连接 , 若 , 则旋转角的度数为( ) A、 B、 C、 D、5. 如图,在△ABC中,AB<AC,将△ABC以点A为旋转中心逆时针旋转得到△ADE,点D在BC边上,DE交AC于点F,则下列结论中错误的是( )
A、 B、 C、 D、5. 如图,在△ABC中,AB<AC,将△ABC以点A为旋转中心逆时针旋转得到△ADE,点D在BC边上,DE交AC于点F,则下列结论中错误的是( ) A、△AFE∽△DFC B、AD=AF C、DA平分∠BDE D、∠CDF=∠BAD6. 如图,在平面直角坐标系中,已知点 , 点A在第一象限内, , , 将绕点О逆时针旋转,每次旋转90°,则第2023次旋转结束时,点A的坐标为( )
A、△AFE∽△DFC B、AD=AF C、DA平分∠BDE D、∠CDF=∠BAD6. 如图,在平面直角坐标系中,已知点 , 点A在第一象限内, , , 将绕点О逆时针旋转,每次旋转90°,则第2023次旋转结束时,点A的坐标为( ) A、 B、 C、 D、7. 如图,△COD是△AOB绕点O顺时针方向旋转30°后所得的图形,点C恰好在AB上,则∠A的度数为( )
A、 B、 C、 D、7. 如图,△COD是△AOB绕点O顺时针方向旋转30°后所得的图形,点C恰好在AB上,则∠A的度数为( ) A、30° B、60° C、70° D、75°8. 下列图形绕某点旋转后,能与原来图形重合的是( )A、
A、30° B、60° C、70° D、75°8. 下列图形绕某点旋转后,能与原来图形重合的是( )A、 B、
B、 C、
C、 D、
D、 9. 如图,将线段绕一个点顺时针旋转得到线段 , 则这个点是( )
9. 如图,将线段绕一个点顺时针旋转得到线段 , 则这个点是( )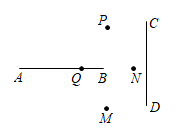 A、点 B、点 C、点 D、点10. 将正方形绕其对称中心旋转后,恰好能与原来的正方边形重合,那么旋转的角度至少是( )A、 B、 C、 D、
A、点 B、点 C、点 D、点10. 将正方形绕其对称中心旋转后,恰好能与原来的正方边形重合,那么旋转的角度至少是( )A、 B、 C、 D、二、填空题
-
11. 如图∆DEF是由∆ABC绕着某点旋转得到的,则这点的坐标是.
 12. 如图,已知 , 点P、A分别为射线、射线上的动点,将射线绕点P逆时针旋转交射线于点B,则的最大值为.
12. 如图,已知 , 点P、A分别为射线、射线上的动点,将射线绕点P逆时针旋转交射线于点B,则的最大值为. 13. 如图,在平面直角坐标系xOy中,直线与坐标轴交于A,B两点,于点C,P是线段OC上的一个动点,连接AP,将线段AP绕点A逆时针旋转 , 得到线段 , 连接 , 则线段的最小值为 .
13. 如图,在平面直角坐标系xOy中,直线与坐标轴交于A,B两点,于点C,P是线段OC上的一个动点,连接AP,将线段AP绕点A逆时针旋转 , 得到线段 , 连接 , 则线段的最小值为 .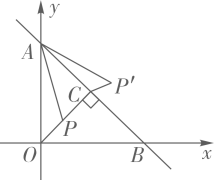 14. 把一个正多边形绕它的中心旋转36°后能与原来的位置重合,则这个多边形的边数至少是 .15. 在冬奥会单板滑雪项目中,运动员的空中姿态优美飘逸.如图,在平面直角坐标系中,将我国运动员的初始位置用△ABC标记,则他在空中的运动可看成从初始位置绕某旋转中心逆时针旋转一定角度后到达另一位置,记为△A′B′C′,在这一过程中,旋转中心的坐标是 .
14. 把一个正多边形绕它的中心旋转36°后能与原来的位置重合,则这个多边形的边数至少是 .15. 在冬奥会单板滑雪项目中,运动员的空中姿态优美飘逸.如图,在平面直角坐标系中,将我国运动员的初始位置用△ABC标记,则他在空中的运动可看成从初始位置绕某旋转中心逆时针旋转一定角度后到达另一位置,记为△A′B′C′,在这一过程中,旋转中心的坐标是 .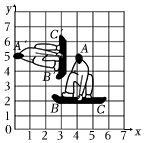
三、解答题
-
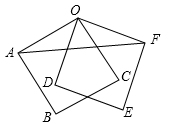
16. 如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,求∠OFA的度数
 17. 如图,在中, , 将绕点A顺时针方向旋转到的位置,连接 , 求的度数.
17. 如图,在中, , 将绕点A顺时针方向旋转到的位置,连接 , 求的度数.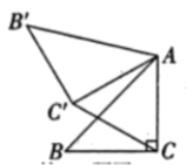 18. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,的三个顶点坐标分别为 .
18. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,的三个顶点坐标分别为 .
( 1 )画出关于x轴对称的 , 并写出点的坐标;
( 2 )画出绕点O顺时针旋转后得到的 , 并写出点的坐标;
( 3 )在(2)的条件下,求点A旋转到点所经过的路径长(结果保留).
四、综合题
-
19. 如图,正方形的边长为6,旋转一定角度后得到 , .
 (1)、旋转中心是点 , 旋转角是;(2)、在图中连接 , 并求出的长.20. 图①、图②、图③均是的正方形网格,每个小正方形的顶点称为格点,线段AB、BC的端点均在格点上,只用无刻度的直尺,在给定的网格中按下列要求以AB、BC为邻边画四边形,使第四个顶点在格点上.
(1)、旋转中心是点 , 旋转角是;(2)、在图中连接 , 并求出的长.20. 图①、图②、图③均是的正方形网格,每个小正方形的顶点称为格点,线段AB、BC的端点均在格点上,只用无刻度的直尺,在给定的网格中按下列要求以AB、BC为邻边画四边形,使第四个顶点在格点上. (1)、在图①中画一个中心对称的四边形ABCD.(2)、在图②中画一个轴对称的四边形ABCE.(3)、在图③中画一个非轴对称的四边形ABCF,且使 .21. 旋转变换在平面几何中有着广泛的应用.特别是在解(证)有关等腰三角形、正三角形、正方形等问题时,更是经常用到的思维方法,请你用旋转交换等知识,解决下面的问题.
(1)、在图①中画一个中心对称的四边形ABCD.(2)、在图②中画一个轴对称的四边形ABCE.(3)、在图③中画一个非轴对称的四边形ABCF,且使 .21. 旋转变换在平面几何中有着广泛的应用.特别是在解(证)有关等腰三角形、正三角形、正方形等问题时,更是经常用到的思维方法,请你用旋转交换等知识,解决下面的问题.如图1,△ABC与△DCE均为等腰直角三角形,DC与AB交于点M,CE与AB交于点N.
 (1)、以点C为中心,将△ACM逆时针旋转90°,画出旋转后的△A′CM′(2)、在(1)的基础上,证明AM2+BN2=MN2 .(3)、如图2,在四边形ABCD中,∠BAD=45°,∠BCD=90°,AC平分∠BCD,若BC=4,CD=3,则对角线AC的长度为多少?(直接写出结果即可,但在图中保留解决问题的过程中所作辅助线、标记的有关计算数据等)22. 如图,在中, , D为AB上的一点,交AC于点E.
(1)、以点C为中心,将△ACM逆时针旋转90°,画出旋转后的△A′CM′(2)、在(1)的基础上,证明AM2+BN2=MN2 .(3)、如图2,在四边形ABCD中,∠BAD=45°,∠BCD=90°,AC平分∠BCD,若BC=4,CD=3,则对角线AC的长度为多少?(直接写出结果即可,但在图中保留解决问题的过程中所作辅助线、标记的有关计算数据等)22. 如图,在中, , D为AB上的一点,交AC于点E. (1)、如图1,由题意可得:;(2)、如图2,将图1中的逆时针旋转到 , 连结BF、CG.求证:;(3)、如图3,将图1中的逆时针继续旋转到 , 且 , 连结与AC相交于点H,连结 , 与交于点O,若 , , 求AO的长.23. 如图,在边长均为1个单位长度的小正方形组成的网格中,点 , , 均为格点(每个小正方形的顶点叫做格点).
(1)、如图1,由题意可得:;(2)、如图2,将图1中的逆时针旋转到 , 连结BF、CG.求证:;(3)、如图3,将图1中的逆时针继续旋转到 , 且 , 连结与AC相交于点H,连结 , 与交于点O,若 , , 求AO的长.23. 如图,在边长均为1个单位长度的小正方形组成的网格中,点 , , 均为格点(每个小正方形的顶点叫做格点).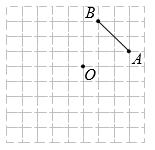 (1)、作点关于点的对称点;(2)、连接 , 将线段绕点顺时针旋转得到线段 , 点的对应点为 , 画出旋转后的线段;(3)、连接 , , 求出的面积(直接写出结果即可).
(1)、作点关于点的对称点;(2)、连接 , 将线段绕点顺时针旋转得到线段 , 点的对应点为 , 画出旋转后的线段;(3)、连接 , , 求出的面积(直接写出结果即可).