（华师大版）2022-2023学年七年级数学下册10.2 平移同步测试

试卷更新日期：2023-03-13 类型：同步测试

进入出卷网下载

一、单选题

1. 如图，正方形网格中，能由 $a$ 平移得到的线段是（）

A、 $b$ B、 $c$ C、 $d$ D、 $e$

查看试题解析
2. 2022年，中国成功举办了第二十四届冬季奥林匹克运动会，吉祥物“冰墩墩”好可爱．如图，通过平移最左边的吉样物“冰墩墩”可以得到的图形是（　　）

A、 B、 C、 D、

查看试题解析
3. 下列每组图形中，左边的图形平移后可以得到右边图形的是（）

A、 B、 C、 D、

查看试题解析
4. 下列现象中，属于平移现象的是（）

A、方向盘的转动 B、行驶的自行车的车轮的运动 C、电梯的升降 D、钟摆的运动

查看试题解析
5. 如图，在边长为1的小正方形组成的网格中，点A，B，C都在格点上，若将线段AB沿BC方向平移，使点B与点C重合，则线段AB扫过的面积为（）

A、11 B、10 C、9 D、8

查看试题解析
6. 如图，把△ABC沿AC方向平移2cm得到△FDE，AE=7cm，则FC的长是（）cm

A、2 B、3 C、4 D、5

查看试题解析
7. 如图， $Δ A B C$ 是直角三角形，它的直角边 $A B = 6$ ， $B C = 8$ ，将 $Δ A B C$ 沿边BC的方向平移到 $Δ D E F$ 的位置，DE交AC于点G， $B E = 2$ ， $Δ C E G$ 的面积为13.5，下列结论：① $Δ A B C$ 平移的距离是4：② $D G = 1.5$ ；③AD $∥$ CF；④四边形ADFC的面积为6．其中正确的结论是（）

A、①② B、②③ C、③④ D、②④

查看试题解析
8. 如图，将 $△ A B C$ 沿直线 $A B$ 向右平移后到达 $△ B D E$ 的位置，连接 $C E$ ，则下面的结论：① $A C ∥ B E$ ② $∠ A C B = ∠ B E D$ ③ $B D = A B$ ④ $∠ C B E = ∠ B E C$ ⑤ $C E = B D$ ，正确的个数是（）

A、2 B、3 C、4 D、5

查看试题解析
9. 下列关于平移的叙述不正确的是（）

A、一个图形经过平移后图形的形状不变 B、一个三角形经过平移后三角形的周长不变 C、一个三角形经过平移后三角形的面积不变 D、一个三角形平移前后对应点的连线互相平行

查看试题解析
10. 如图，将周长为7的 $△ A B C$ 沿 $B C$ 方向平移1个单位得到 $△ D E F$ ，则四边形 $A B F D$ 的周长是（）

A、11 B、10 C、9 D、8

查看试题解析

二、填空题

11. 如图，三角形ABC向右平移得到三角形DEF，若BC＝6cm，EC＝2cm，则CF＝．

查看试题解析
12. 如图，在一块长为21m，宽为15m的长方形草地上，有一块弯曲的小路，小路的左边线向右平移1m就是它的右边线，则这块草地的绿地面积为m² ．

查看试题解析
13. 如图，在三角形 $A B C$ 中， $A B = 2 B C = 4 c m$ ．把三角形 $A B C$ 沿 $A B$ 方向平移 $1 c m$ ，得到三角形 $A_{1} B_{1} C_{1}$ ，连接 $C C_{1}$ ，则四边形 $B B_{1} C_{1} C$ 的周长为 $c m$ ．

查看试题解析
14. 如图，△ABC沿着由点B到点E的方向平移，得到△DEF，若BC＝4，EC＝1，那么平移的距离是．

查看试题解析
15. 如图，红黄绿三块一样大的正方形纸片放在一个底面为正方形盒内，它们之间互相重叠．已知露在外面的部分中，红色的面积是20，黄色的面积是13，绿色的面积是11，则盒子底面的面积为．

查看试题解析

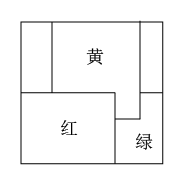
三、解答题

16. 如图，我们将数轴水平放置称为 $x$ 轴，将数轴竖直放置称为 $y$ 轴， $x$ 轴与 $y$ 轴的交点称为原点 $O$ ，由 $x$ 轴、 $y$ 轴及原点 $О$ 就组成了一个平面.若平面上的点作如下平移：沿 $x$ 轴方向平移的数量为 $a$ （向右为正，向左为负，平移 $a$ 个单位），沿 $y$ 轴方向平移的数量为 $b$ （向上为正，向下为负，平移 $b$ 个单位），则把有序数对 ${a ， b}$ 叫做这一平移的“平移量”.动点 $Р$ 从坐标原点出发，先按照“平移量” ${3 ， 1}$ 平移到 $A$ （如图），再按照“平移量” ${1 ， 2}$ 平移到 $B$ ，最后按照“平移量” ${- 3 ， 1}$ 平移到 $C$ .请你画出四边形 $O A B C$ .

查看试题解析
17. 某宾馆重新装修后，准备在大厅的主楼梯上铺设一种红地毯，已知这种地毯每平方米售价50元，主楼梯道宽2m，其侧面如图所示，求买地毯至少需要多少元？

查看试题解析
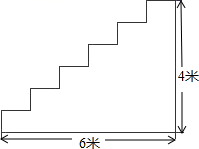18. 如图，△ABC的周长为30㎝，将△ABC沿CB向右平移得到△DEF，若平移的距离为4㎝，则四边形ACED 的周长是多?

查看试题解析

四、综合题

19. 已知：如图，把 $△ A B C$ 向上平移3个单位长度，再向右平移2个单位长度，得到 $△ A^{'} B^{'} C^{'}$ ．

(1)、在图中画出 $△ A^{'} B^{'} C^{'}$ ．

(2)、写出 $A^{'}$ ， $B^{'}$ 的坐标．

(3)、在 $y$ 轴上是否存在一点 $P$ ，使得 $△ B C P$ 与 $△ A B C$ 面积相等？若存在，求出点 $P$ 的坐标；若不存在，说明理由．

查看试题解析
20. 在如图的网格中，A、B、C、E、F为格点，点P在线段EF上．

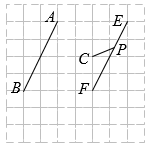(1)、线段AB向右平移格可以得到线段EF；

(2)、过点C画AB的垂线，垂足为D；

(3)、若 $∠ C P E = α °$ ，则∠DCP＝°．（用含 $α$ 的代数式表示）．

查看试题解析
21. 已知 $M N$ // $P Q$ ，点B、C在 $M N$ 上（B在C左侧），A在 $P Q$ 上，连接 $A B$ 、 $A C$ ， $∠ P A B = 60 °$ ， $∠ A C B = 40 °$ ， $A E$ 平分 $∠ P A C$ ， $B E$ 平分 $∠ A B C$ ， $A E$ 、 $B E$ 交于点E．

(1)、求 $∠ A E B$ 的度数；

(2)、若将图1中的线段 $A C$ 沿 $P Q$ 向右平移到 $D C$ 如图2所示位置， $D E$ 平分 $∠ A D C$ ， $B E$ 平分 $∠ A B C$ ， $D E$ 、 $B E$ 交于点E， $∠ P A B = 60 °$ ， $∠ D C B = 40 °$ ，请你直接写出 $∠ D E B$ 的度数：

(3)、若将图1中的线段 $A C$ 沿 $P Q$ 向左平移到 $D C$ 如图3所示位置，其它条件与（2）相同，猜想此时 $∠ D E B$ 的度数又是多少．（不需要证明）

查看试题解析
22. 如图1，AB、BC被直线AC所截，点D是线段AC上的点，过点D作DE∥AB，连接AE，∠B＝∠E＝75°．

(1)、求证：AE∥BC；

(2)、将线段AE沿着直线AC平移得到线段PQ，连接DQ．如图2，当DE⊥DQ时，求∠Q的度数．

查看试题解析
23. 如图，正方形网格中，△ABC为格点三角形．(即三角形的顶点都在格点上)

(1)、按要求作图：将△ABC沿BC方向平移，平移的距离是BC长的3倍，在网格中画出平移后的△A₁B₁C₁

(2)、如果网格中小正方形的边长为1，求△ABC在平移过程中扫过的面积．

查看试题解析

（华师大版）2022-2023学年七年级数学下册10.2 平移 同步测试

一、单选题

二、填空题

三、解答题

四、综合题

（华师大版）2022-2023学年七年级数学下册10.2 平移同步测试