（华师大版）2022-2023学年七年级数学下册9.2多边形的内角和与外角和 同步测试
试卷更新日期：2023-03-12 类型：同步测试
一、单选题
-
1. 一个多边形的内角和的度数可能是（ ）A、1700° B、1800° C、1900° D、2000°2. 下列平面图形中，内角和是1080°的是（ ）A、
B、
C、
D、
3. 若一个多边形的每个内角都等于150°，则这个多边形的边数是（ ）A、9 B、10 C、11 D、124. 如图，在中， ， 则图中的度数是（ ）
A、180° B、240° C、220° D、300°5. 如图，四边形中， ， 与、相邻的两外角平分线交于点E，若 ， 则的度数为（ ）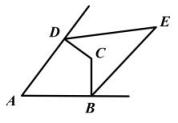
A、45° B、60° C、40° D、50°6. 如图，将三角形纸片ABC沿DE折叠，当点A落在四边形BCDE的外部时，测量得∠1＝70°，∠2＝152°，则∠A为（ ）
A、40° B、42° C、30° D、52°7. 如图，已知直线a∥b，将一副三角板按如图所示放置在两条平行线之间，若∠2＝55°，则∠1的度数是（ ）
A、45° B、65° C、75° D、85°8. “花影遮墙，峰峦叠窗”苏州园林空透的窗棂中蕴含着许多的数学元素.如图是窗棂是冰裂纹窗及这种窗棂中的部分图案.若 ， ，则下列判断中正确的是（ ）
A、 B、 C、 D、 的度数无法确定9. 已知一个多边形的外角和是其内角和的 ，则下列说法正确的是（ ）A、过这个多边形一个顶点可做7条对角线 B、它的内角和为1260° C、如果将它剪掉一个角，则还余下8个角 D、它的每个外角为40°10. 小聪为某机器人编制一段程序，如果机器人以 的速度在平地上按照图中的步骤行走，那么该机器人从开始到停止所需的时间为（ ）
A、 B、 C、 D、二、填空题
-
11. 如图，AB∥CD，∠DCE的角平分线CG的反向延长线和∠ABE的角平分线BF交于点F，∠E﹣∠F=33°，则∠E= ．
12. 若多边形的内角和比外角和大540°，则该多边形的边数是 ．13. 若一个正多边形从一个顶点出发，只可以引3条对角线，则它的每个内角是度．14. 如果过某多边形的一个顶点的对角线有6条，则该多边形一共有条对角线．15. 如图， ．
三、解答题
-
16. 在各个内角都相等的多边形中，一个内角等于一个外角的3倍，求这个多边形的边数和它的内角和．17. 求出下列图形中的值．
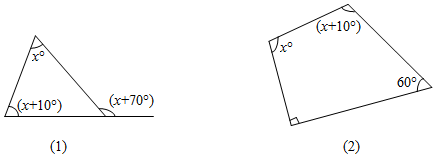18. 已知在一个十边形中，其中九个内角的和是1302°，求这个十边形另一个内角的度数．四、综合题
-
19. 如图，将六边形纸片ABCDEF沿虚线剪去一个角（∠BCD）后，得到∠1+∠2+∠3+∠4+∠5＝470°．
(1)、求六边形ABCDEF的内角和；(2)、求∠BGD的度数．20. 已知一个多边形的内角和比它的外角和的3倍多 ．(1)、求这个多边形是几边形；(2)、如果从这个多边形的一个顶点引出对角线，最多可以引条对角线．21. 如图，在四边形ABCD中，是四边形ABCD的一个外角.
(1)、如图1，试判断与的数量关系，并说明理由；(2)、如图2，若 ， AE平分 ， CF平分 ， 且AE与CF相交于点F，试判断AE与CF的位置关系，并说明理由.22. 直线MN与直线PQ垂直相交于O，点A在射线OP上运动，点B在射线OM上运动．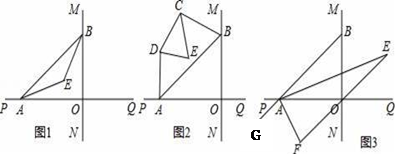
(1)、如图1，已知AE、BE分别是∠BAO和∠ABO角的平分线，点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出∠AEB的大小．(2)、如图2，已知AB不平行CD，AD、BC分别是∠BAP和∠ABM的角平分线，又DE、CE分别是∠ADC和∠BCD的角平分线，点A、B在运动的过程中，∠CED的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值．(3)、如图3，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F，在△AEF中，如果有两个角度数的比是3：2，请直接写出∠ABO的度数 ．23. 已知：直线AB∥CD，M，N分别在直线AB，CD上，H为平面内一点，连HM，HN．
(1)、如图1，延长HN至G，∠BMH和∠GND的角平分线相交于点E．①若∠BME=25°，∠END=75°，则∠H的度数为 ▲ ；
②探究∠MEN与∠MHN的数量关系，并给予证明；
(2)、如图2，∠BMH和∠HND的角平分线相交于点E．作MP平分∠AMH，NQ∥MP交ME的延长线于点Q，若∠H＝150°，求∠ENQ的度数．