(华师大版)2022-2023学年七年级数学下册9.1.1认识三角形 同步测试
试卷更新日期:2023-03-12 类型:同步测试
一、单选题
-
1. 利用直角三角板,作的高线,下列作法正确的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,是的中线,点是上一点,若 , , 则的长为( )
2. 如图,是的中线,点是上一点,若 , , 则的长为( ) A、5 B、6 C、7 D、83. 如图,在△ABC中,AD是△ABC的角平分线,则( )
A、5 B、6 C、7 D、83. 如图,在△ABC中,AD是△ABC的角平分线,则( )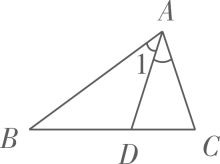 A、∠1=∠BAC B、∠1=∠ABC C、∠1=∠BAC D、∠1=∠ABC4. 下列各图中,正确画出 边上的高的是( )A、
A、∠1=∠BAC B、∠1=∠ABC C、∠1=∠BAC D、∠1=∠ABC4. 下列各图中,正确画出 边上的高的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,是的中线,则下列结论正确的是( )
5. 如图,是的中线,则下列结论正确的是( ) A、 B、 C、 D、6. 如图,是的中线, , 则的长为( )
A、 B、 C、 D、6. 如图,是的中线, , 则的长为( )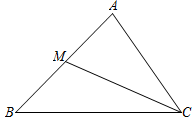 A、 B、 C、 D、7. 如图,在△ABC中,作BC边上的高线,下列画法正确的是( )A、
A、 B、 C、 D、7. 如图,在△ABC中,作BC边上的高线,下列画法正确的是( )A、 B、
B、 C、
C、 D、
D、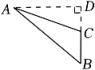 8. 下列图形中,线段表示的高线的是( )A、
8. 下列图形中,线段表示的高线的是( )A、 B、
B、 C、
C、 D、
D、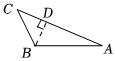 9. 下列各个图形中,是的高的是( )A、
9. 下列各个图形中,是的高的是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,是的中线,已知的周长为25cm,比长7cm,则的周长( )
10. 如图,是的中线,已知的周长为25cm,比长7cm,则的周长( )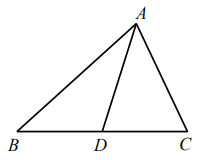 A、18cm B、22cm C、19cm D、31cm
A、18cm B、22cm C、19cm D、31cm二、填空题
-
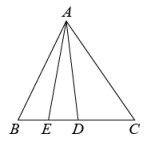
11. 已知点是的重心,那么12. 已知、是的高,直线、相交所成的锐角为40°,则的度数是 .13. 已知在中,是中线,是重心,如果 , 那么 .14. 已知点G是等腰直角三角形的重心, , 那么AG的长为 .15. 如图,是的中线,是的中线,若 , 则 .
三、解答题
-
16. 如图,在三角形中, , , 是的中点,点在边上.若三角形的周长与四边形的周长相等,求线段的长.
 17. 如图,在ABC中,AD是ABC的高,AE、BF是ABC角平分线,AE与BF相交于点O,∠BOA=125°,求∠DAC的度数.
17. 如图,在ABC中,AD是ABC的高,AE、BF是ABC角平分线,AE与BF相交于点O,∠BOA=125°,求∠DAC的度数. 18. 如图,在中,是的角平分线,是边上的高,相交于点O,如果 , 求的度数.
18. 如图,在中,是的角平分线,是边上的高,相交于点O,如果 , 求的度数.
四、综合题
-
19. 如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°.
 (1)、求∠DAE的度数;(2)、试写出 ∠DAE与∠C-∠B有何关系? 关系为: .20. 如图,分别是的高线、角平分线和中线.
(1)、求∠DAE的度数;(2)、试写出 ∠DAE与∠C-∠B有何关系? 关系为: .20. 如图,分别是的高线、角平分线和中线. (1)、有下列结论:①;②;③;④与互余.其中正确的是(填序号).(2)、若 , 求的度数.21. 如图,在三角形ABC中,AB=10cm,AC=6cm,D是BC的中点,E点在边AB上.
(1)、有下列结论:①;②;③;④与互余.其中正确的是(填序号).(2)、若 , 求的度数.21. 如图,在三角形ABC中,AB=10cm,AC=6cm,D是BC的中点,E点在边AB上. (1)、若三角形BDE的周长与四边形ACDE的周长相等,求线段AE的长.(2)、若三角形ABC的周长被DE分成的两部分的差是2,求线段AE的长.
(1)、若三角形BDE的周长与四边形ACDE的周长相等,求线段AE的长.(2)、若三角形ABC的周长被DE分成的两部分的差是2,求线段AE的长.

