(华师大版)2022-2023学年七年级数学下册8.3 一元一次不等式组 同步测试
试卷更新日期:2023-03-12 类型:同步测试
一、单选题
-
1. 关于x的不等式组恰好有3个整数解,则a满足( )A、 B、 C、 D、2. 若不等式组的解集是x<2,则m的取值范围是( )A、m=2 B、m≥2 C、m<2 D、m>23. 如图是测量一颗玻璃球体积的过程:

(1)将的水倒进一个容量为的杯子中;
(2)将五颗相同的玻璃球放入水中,结果水没有满;
(3)再加一颗同样的玻璃球放入水中,结果水满溢出.根据以上过程,推测这样一颗玻璃球的体积范围是( )
A、以上,以下 B、以上,以下 C、以上,以下 D、以上,以下4. 不等式组的解集在数轴上用阴影表示正确的是( )A、 B、
B、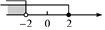 C、
C、 D、
D、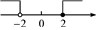 5. 如果关于的不等式组的解集为 , 且关于的分式方程有非负数解,则所有符合条件的整数的值之和是( )A、-2 B、0 C、3 D、56. 不等式组的解集是( )A、 B、 C、或 D、7. 不等式组的最小整数解为( )A、 B、 C、 D、8. 若关于x的不等式组只有4个整数解,则a的取值范围是( )A、 B、 C、 D、9. 若关于x的不等式组有解,且关于x的分式方程有非负整数解,则满足条件的所有整数m的和为( )A、9 B、10 C、11 D、1210. 关于x的不等式组的解集为 , 且关于y的分式方程的解为正数,则所有满足条件的整数m的值之和为( )A、3 B、4 C、5 D、6
5. 如果关于的不等式组的解集为 , 且关于的分式方程有非负数解,则所有符合条件的整数的值之和是( )A、-2 B、0 C、3 D、56. 不等式组的解集是( )A、 B、 C、或 D、7. 不等式组的最小整数解为( )A、 B、 C、 D、8. 若关于x的不等式组只有4个整数解,则a的取值范围是( )A、 B、 C、 D、9. 若关于x的不等式组有解,且关于x的分式方程有非负整数解,则满足条件的所有整数m的和为( )A、9 B、10 C、11 D、1210. 关于x的不等式组的解集为 , 且关于y的分式方程的解为正数,则所有满足条件的整数m的值之和为( )A、3 B、4 C、5 D、6二、填空题
-
11. 若关于x的不等式组有且仅有一个整数解 , 则实数a的取值范围是.12. 不等式组的所有整数解的和为 .13. 定义:对于实数a,符号表示不大于a的最大整数.例如: , , .如果 , 则满足条件的所有正整数x的值是.14. 运行程序如图所示,规定:从“输入一个值”到“结果是否”为一次程序操作,如果程序操作进行了三次才停止,那么的取值范围是.
 15. 我们用表示不小于a的最小整数,例如: , , .若 , 则x的取值范围是.
15. 我们用表示不小于a的最小整数,例如: , , .若 , 则x的取值范围是.三、解答题
-
16. 求不等式组的最大整数解.17. 解一元一次不等式组 , 并把解表示在数轴上.
 18. 已知关于x、y的方程组的解x,y都是正数,求m的取值范围.
18. 已知关于x、y的方程组的解x,y都是正数,求m的取值范围.四、综合题
-
19. 某社区为了更好地开展“垃圾分类,美丽永州”活动,需购买A,B两种类型垃圾桶,用1600元可购进A型垃圾桶14个和B型垃圾桶8个,且购买3个A型垃圾桶的费用与购买4个B型垃圾桶的费用相同,请解答下列问题:(1)、求出A型垃圾桶和B型垃圾桶的单价.(2)、若社区欲用不超过3600元购进两种垃圾桶共50个,其中A型垃圾桶至少29个,求有哪几种购买方案?20. 解不等式(组)(1)、3y-2≤6+7y,并把解集表示在数轴上
 (2)、解不等式组21. 某公司需将一批材料运往工厂,计划租用甲、乙两种型号的货车,在每辆货车都满载的情况下,甲型货车每辆装载量是乙型货车的倍,若甲、乙两种型号货车各装载1500箱材料,甲型货车比乙型货车少用40辆.(1)、甲、乙两种型号的货车每辆分别可装载多少箱材料?(2)、经初步估算,公司要运往工厂的这批材料不超过1100箱.计划租用甲、乙两种型号的货车共60辆,且乙型货车的数量不大于甲型货车数量的2倍,该公司一次性将这批材料运往工厂共有哪几种租车方案?22. 某体育用品店准备购进甲,乙品牌乒乓球两种,若购进甲种乒乓球10个,乙种乒乓球5个,需要100元,若购进甲种乒乓球5个,乙种乒乓球3个,需要55元.(1)、求购进甲,乙两种乒乓球每个各需多少元?(2)、若该体育用品店刚好用了1000元购进这两种乒乓球,考虑顾客需求,要求购进甲种乒乓球的数量不少于乙种乒乓球数量的6倍,且乙种乒乓球数量不少于23个,那么该文具店共有哪几种进货方案?(3)、若该体育用品店销售每只甲种乒乓球可获利润3元,销售每只乙种乒乓球可获利润4元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?23. 随着全国疫情防控取得阶段性进展,各学校进一步做好疫情防控工作.为方便师生测体温,某校计划购买A、B两种额温枪.经调研得知:购买1个A型额温枪和2个B型额温枪共需800元,购买2个A型额温枪和3个B型额温枪共需1300元.(1)、求每个A型额温枪和B型额温枪各多少元;(2)、若该学校准备购买A、B两种型号的额温枪共50个(每种型号至少买一只);要求总费用不超过12800元,则对购买A型号的额温枪在数量上有什么要求?说明理由.(3)、在(2)的条件下,若甲、乙两商店以同样价格出售这两种型号的额温枪,同时又各自推出不同的优惠方案:在甲店购买A型额温枪按原价90%收费,B型额温枪不优惠;在乙店购买A型额温枪不优惠,但购买B型额温枪按原价90%收费;则学校到哪家商店购买额温枪花费少?
(2)、解不等式组21. 某公司需将一批材料运往工厂,计划租用甲、乙两种型号的货车,在每辆货车都满载的情况下,甲型货车每辆装载量是乙型货车的倍,若甲、乙两种型号货车各装载1500箱材料,甲型货车比乙型货车少用40辆.(1)、甲、乙两种型号的货车每辆分别可装载多少箱材料?(2)、经初步估算,公司要运往工厂的这批材料不超过1100箱.计划租用甲、乙两种型号的货车共60辆,且乙型货车的数量不大于甲型货车数量的2倍,该公司一次性将这批材料运往工厂共有哪几种租车方案?22. 某体育用品店准备购进甲,乙品牌乒乓球两种,若购进甲种乒乓球10个,乙种乒乓球5个,需要100元,若购进甲种乒乓球5个,乙种乒乓球3个,需要55元.(1)、求购进甲,乙两种乒乓球每个各需多少元?(2)、若该体育用品店刚好用了1000元购进这两种乒乓球,考虑顾客需求,要求购进甲种乒乓球的数量不少于乙种乒乓球数量的6倍,且乙种乒乓球数量不少于23个,那么该文具店共有哪几种进货方案?(3)、若该体育用品店销售每只甲种乒乓球可获利润3元,销售每只乙种乒乓球可获利润4元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?23. 随着全国疫情防控取得阶段性进展,各学校进一步做好疫情防控工作.为方便师生测体温,某校计划购买A、B两种额温枪.经调研得知:购买1个A型额温枪和2个B型额温枪共需800元,购买2个A型额温枪和3个B型额温枪共需1300元.(1)、求每个A型额温枪和B型额温枪各多少元;(2)、若该学校准备购买A、B两种型号的额温枪共50个(每种型号至少买一只);要求总费用不超过12800元,则对购买A型号的额温枪在数量上有什么要求?说明理由.(3)、在(2)的条件下,若甲、乙两商店以同样价格出售这两种型号的额温枪,同时又各自推出不同的优惠方案:在甲店购买A型额温枪按原价90%收费,B型额温枪不优惠;在乙店购买A型额温枪不优惠,但购买B型额温枪按原价90%收费;则学校到哪家商店购买额温枪花费少?