鲁教版（五四学制）2022-2023学年八年级数学下册9.7 利用相似三角形测高 同步测试
试卷更新日期：2023-03-12 类型：同步测试
一、单选题
-
1. 如图，线段AB，EF，CD分别表示人，竹竿，楼房的高度，且A，E，C在同一直线上．测得人和竹竿的水平距离为1.2m，人和楼房的水平距离为20m，人的高度为1.5m，竹竿的高度为3m，则楼房的高度是（ ）
A、25m B、26.5m C、50m D、51.5m2. 大约在两千五百年前，如图1墨子和他的学生做了世界上第1个小孔成倒像的实验．并在《墨经》中有这样的精彩记录：“景到，在午有端，与景长，说在端”．如图2所示的小孔成像实验中，若物距为10cm，像距为15cm，蜡烛火焰倒立的像的高度是9cm，则蜡烛火焰的高度是（ ）
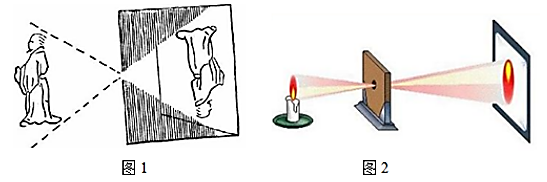A、6cm B、8cm C、10cm D、12cm3. “跳眼法”是炮兵常用的一种简易测距方法，如图，点A为左眼，点B为右眼，点O为右手大拇指，点C为敌人的位置，点D为敌人正左侧方的某一个参照物 ， 已知大多数人的眼距长约为6.4厘米左右，而手臂长约为64厘米左右．若的估测长度为50米，那么的大致距离为（ ）米．
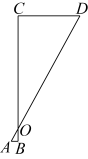A、250 B、320 C、500 D、7504. 如图，路灯距离地面8米，若身高1.6米的小明在路灯下处测得影子的长为5米，则小明和路灯的距离为（ ）
A、25米 B、15米 C、16米 D、20米5. 如图，小红利用小孔成像原理制作了一个成像装置，他在距离纸筒处准备了一支蜡烛，其中纸筒长为 ， 蜡烛长为 ， 则这支蜡烛所成像的高度为（ ）
A、 B、 C、 D、6. 如图，测量小玻璃管口径的量具ABC，AB的长为3cm，AC被分为6等份．若小玻璃管口DE正好对着量具上2等份处（DE∥AB），那么小玻璃管口径DE的长为（ ）
A、1cm B、cm C、2cm D、cm7. 国旗法规定：所有国旗均为相似矩形，在下列四面国旗中，其中只有一面不符合标准，这面国旗是（ ）A、
B、
C、
D、
8. 如图，广场上有一盏路灯挂在高的电线杆顶上，记电线杆的底部为 ． 把路灯看成一个点光源，一名身高的女孩站在点处， ， 则女孩的影子长为（ ）
A、 B、 C、 D、9. 如图，小红利用小孔成像原理制作了一个成像装置，他在距离纸筒处准备了一支蜡烛，蜡烛长为 ， 纸筒的长度为 ， 则这支蜡烛所成像的高度为（ ）
A、 B、 C、 D、10. 如图所示为我市某农村一古老的捣碎器，已知支撑柱AB的高为0.3米，踏脚着地时捣头点E距离地面0.8米 ，则捣头点E着地时，踏脚点D距离地面（ ）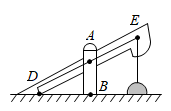
A、0.4 米 B、0.48米 C、0.5 米 D、0.8米二、填空题
-
11. 如图，路灯距离地面 ， 身高的小明站在距离灯的底部（点）的处，则小明的影子的长为m.
12. 大约在两千四五百年前，如图1墨子和他的学生做了世界上第1个小孔成倒像的实验．并在《墨经》中有这样的精彩记录：“景到，在午有端，与景长，说在端”．如图2所示的小孔成像实验中，若物距为10cm，像距为15cm，蜡烛火焰倒立的像的高度是9cm，则蜡烛火焰的高度是 cm．
13. 如图所示，某校数学兴趣小组利用自制的直角三角形硬纸板来测量操场旗杆的高度，他们通过调整测量位置，使斜边与地面保持平行，并使边与旗杆顶点在同一直线上，已知米，米，目测点到地面的距离米，到旗杆水平的距离米，则旗杆的高度为米．
14. 如图所示，某校数学兴趣小组利用标杆测量建筑物的高度，已知标杆高m，测得m，m．则建筑物的高是m．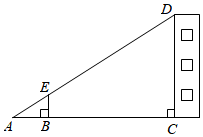
15. 测量附中国旗杆的高度，小宇的测量方法如下：如图，将直角三角形硬纸板△DEF的斜边DF与地面保持平行，并使边DE与旗杆顶点A在同一直线上．测得DE＝0.5米，EF＝0.25米，目测点D到地面的距离DG＝1.6米，到旗杆的水平距离DC＝18米．按此方法，可计算出旗杆的高度为 米．
三、解答题
-
16. 为测量一棵大树的高度，设计的测量方案如图所示：标杆高度 ， 人的眼睛A、标杆的顶端C和大树顶端M在一条直线上，标杆与大树的水平距离 ， 人的眼睛与地面的高度 ， 人与标杆的水平距离 ， B、D、N三点共线， ， 求大树的高度.
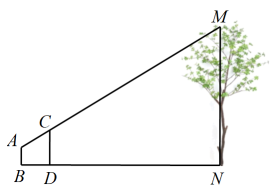17. 某校同学参与“项目式学习”综合实践活动，小明所在的数学活动小组利用所学知识测量旗杆EF的高度，他在距离旗杆40米的D处立下一根3米高的竖直标杆CD，然后调整自己的位置，当他与标杆的距离BD为4米时，他的眼睛、标杆顶端和旗杆顶位于同一直线上，若小明的眼睛离地面高度AB为1.6米，求旗杆EF的高度．
18. 如图是某数学兴趣小组设计用手电筒来测量某古城墙高度的示意图，在点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处，CD⊥BD，且测得AB＝4m，BP＝6m，PD＝12m，求该古城墙CD的高度是多少m？
四、综合题
-
19. 如图1，长、宽均为3cm，高为8cm的长方体容器，放置在水平桌面上，里面盛有水，水面高为6cm，绕底面一棱进行旋转倾斜后，水面恰好触到容器口边缘，图2是此时的示意图，将这个情景转化成几何图形，如图3所示．
(1)、利用图1、图2所示水的体积相等，求的长；(2)、求水面高度 ．20. 我们知道当人们的视线与物体的表面互相垂直且视线恰好落在物体中心位置时的视觉效果最佳，如图是小然站在地面MN欣赏悬挂在墙壁PM上的油画AD（PM⊥MN）的示意图，设油画AD与墙壁的夹角∠PAD＝α，此时小然的眼睛与油画底部A处于同一水平线上，视线恰好落在油画的中心位置E处，且与AD垂直．已知油画的长度AD为100cm．
(1)、视线∠ABD的度数为 .（用含α的式子表示）(2)、当小然到墙壁PM的距离AB＝250cm时，求油画顶部点D到墙壁PM的距离．21. 学习了相似三角形相关知识后，小明和同学们想利用“标杆”测量大楼的高度．如图，小明站立在地面点F处，他的同学在点B处竖立“标杆” ， 使得小明的头顶点E、杆顶点A、楼顶点C在一条直线上（点F、B、D也在一条直线上）．已知小明的身高米，“标杆”米，又米，米．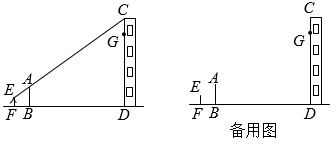
(1)、求大楼的高度为多少米（垂直地面）？(2)、小明站在原来的位置，同学们通过移动标杆，可以用同样的方法测得楼上点G的高度米，那么相对于第一次测量，标杆应该向大楼方向移动米.22. 小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高．如图所示，在某一时刻，他们在阳光下，分别测得该建筑物的影长为16米，的影长为20米，小明的影长为2.4米，其中O、C、D、F、G五点在同一直线上，A、B、O三点在同一直线上，且 ， ． 已知小明的身高为1.8米．
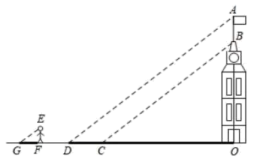(1)、求建筑物OB的高度；(2)、求旗杆的高AB．23. 如图为幸福小区入口处安装的汽车出入道闸示意图．如图1，道闸关闭时，四边形是矩形．如图2，在道闸打开的过程中，边固定，直线l，连杆、分别绕点A、D转动，且边始终与边平行，P为上的一点（不与点C，D重合），过点P作直线l， ， 垂足分别为E，F，即四边形是矩形，过点D作 ， 垂足为Q，延长与相交于点R．
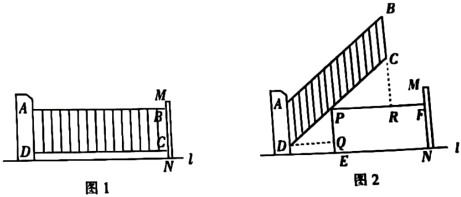(1)、与相似吗？请判断并说明理由．(2)、若道闸长米，宽米，点D距地面米，米，米，米．①求点B到地面l的距离；
②求的长．