鲁教版(五四学制)2022-2023学年八年级数学下册9.6 黄金分割 同步测试
试卷更新日期:2023-03-12 类型:同步测试
一、单选题
-
1. 若点C是线段AB的黄金分割点, , 则AC的长度为( )A、 B、 C、5 D、2. 比值为(约0.618)的比例被公认为是最能引起美感的比例,因此被称为黄金分割比,我们中国的国旗宽与长之比就非常接近这个比例,如果某面国旗长为2米,则其宽约为( )A、1.5米 B、1.2米 C、1.0米 D、0.8米3. 神奇的自然界处处隐含着数学美!生物学家在向日葵圆盘中发现:向日葵籽粒成螺线状排列,螺线的发散角是 . 我们知道圆盘一周为 , , . 这体现了( )
 A、轴对称 B、旋转 C、平移 D、黄金分割4. 下面说法错误的是( )A、点 , 都在反比例函数图象上,且 , 则 B、若点是线段的黄金分割点, , , 则 C、顺次连接对角线互相垂直的四边形各边中点所组成的图形是矩形 D、平面内,经过平行四边形对角线交点的直线,一定能平分它的面积5. 已知点C是线段AB的黄金分割点(AC>BC),若AB=4,则AC的长为( )A、(6-2) B、(2-2) C、(-1) D、(3-)6. 一本书的宽与长之比为黄金比,书的宽为14cm,则它的长为( )cmA、 B、 C、 D、7. 一般认为,如果一个人的肚脐以上的高度与肚脐以下的高度符合黄金分割,则这个人身材好.如图,是一个参加空姐选拔的选手的实际身高情况,如果要使身材好,那么她穿鞋子的高度最好为( ) . (精确到 , 参考数据:黄金分割比为)
A、轴对称 B、旋转 C、平移 D、黄金分割4. 下面说法错误的是( )A、点 , 都在反比例函数图象上,且 , 则 B、若点是线段的黄金分割点, , , 则 C、顺次连接对角线互相垂直的四边形各边中点所组成的图形是矩形 D、平面内,经过平行四边形对角线交点的直线,一定能平分它的面积5. 已知点C是线段AB的黄金分割点(AC>BC),若AB=4,则AC的长为( )A、(6-2) B、(2-2) C、(-1) D、(3-)6. 一本书的宽与长之比为黄金比,书的宽为14cm,则它的长为( )cmA、 B、 C、 D、7. 一般认为,如果一个人的肚脐以上的高度与肚脐以下的高度符合黄金分割,则这个人身材好.如图,是一个参加空姐选拔的选手的实际身高情况,如果要使身材好,那么她穿鞋子的高度最好为( ) . (精确到 , 参考数据:黄金分割比为)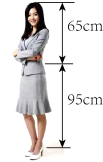 A、5 B、8 C、10 D、128. 大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”.如图,P为AB的黄金分割点 , 如果AB的长度为8cm,那么AP的长度是( )cm.
A、5 B、8 C、10 D、128. 大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”.如图,P为AB的黄金分割点 , 如果AB的长度为8cm,那么AP的长度是( )cm. A、 B、 C、 D、9. 如果P是线段的黄金分割点,并且 , , 那么的长度为( )A、 B、 C、 D、10. 点P是线段的黄金分割点,且 , 则下列等式不成立的是( )A、 B、 C、 D、
A、 B、 C、 D、9. 如果P是线段的黄金分割点,并且 , , 那么的长度为( )A、 B、 C、 D、10. 点P是线段的黄金分割点,且 , 则下列等式不成立的是( )A、 B、 C、 D、二、填空题
-
11. 如图,在“黄金三角形”中, , , 平分交于点D,若 , 则的长为 .
 12. 在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比,已知这本书的长为 , 则它的宽为.(结果保留根号)13. 黄金分割总能给人以美的享受,从人体审美学的角度看,若一个人上半身长与下半身长之比满足黄金比的话,则此人符合和谐完美的身体比例.一芭蕾舞演员的身高为160cm,但其上半身长与下半身长之比大于黄金比,当其表演时掂起脚尖,身高就可以增加10cm,这时上半身长与下半身长之比就恰好满足黄金比,那么该演员的上半身长为cm.(结果保留根号)
12. 在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比,已知这本书的长为 , 则它的宽为.(结果保留根号)13. 黄金分割总能给人以美的享受,从人体审美学的角度看,若一个人上半身长与下半身长之比满足黄金比的话,则此人符合和谐完美的身体比例.一芭蕾舞演员的身高为160cm,但其上半身长与下半身长之比大于黄金比,当其表演时掂起脚尖,身高就可以增加10cm,这时上半身长与下半身长之比就恰好满足黄金比,那么该演员的上半身长为cm.(结果保留根号) 14. 若线段AB=10,且点C是AB的黄金分割点,且BC>AC,则BC的长为 .15. 已知线段 , 是线段的黄金分割点, , 则 .
14. 若线段AB=10,且点C是AB的黄金分割点,且BC>AC,则BC的长为 .15. 已知线段 , 是线段的黄金分割点, , 则 .三、解答题
-
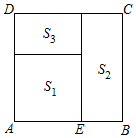
16. 如图,点E是正方形 的边 边上的黄金分割点,且 > , 表示 为边长的正方形面积, 表示以 为长, 为宽的矩形面积, 表示正方形 除去 和 剩余的面积,求 : 的值.
 17. 如图,在平行四边形ABCD中,E为边AD延长线上的一点,且D为AE的黄金分割点,即 ,BE交DC于点F,已知 ,求CF的长 .
17. 如图,在平行四边形ABCD中,E为边AD延长线上的一点,且D为AE的黄金分割点,即 ,BE交DC于点F,已知 ,求CF的长 . 18. 如图,已知等腰△ABC中,顶角∠A=36°,BD为∠ABC的平分线,求证:点D是AC的黄金分割点.
18. 如图,已知等腰△ABC中,顶角∠A=36°,BD为∠ABC的平分线,求证:点D是AC的黄金分割点.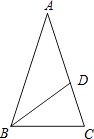
四、综合题
-
19.(1)、已知a=4.5,b=2,c是a,b的比例中项,求c;(2)、如图,C是AB的黄金分割点,且AC>BC,AB=4,求AC的长.
 20.(1)、已知 , 求的值;(2)、已知点P是线段AB的黄金分割点,PA>PB,AB=2,求PA、PB的长.21. 如图,已知在△ABC中,BC>AB , BD平分∠ABC , 交边AC于点D , E是BC边上一点,且BE=BA , 过点A作AG∥DE , 分别交BD、BC于点F、G , 联结FE .
20.(1)、已知 , 求的值;(2)、已知点P是线段AB的黄金分割点,PA>PB,AB=2,求PA、PB的长.21. 如图,已知在△ABC中,BC>AB , BD平分∠ABC , 交边AC于点D , E是BC边上一点,且BE=BA , 过点A作AG∥DE , 分别交BD、BC于点F、G , 联结FE . (1)、求证:四边形AFED是菱形;(2)、求证:AB2=BG•BC;(3)、若AB=AC , BG=CE , 联结AE , 求 的值.22. 已知在△ABC中,AB=AC= ,∠BAC=120°,△ADE的顶点D在边BC上,AE交BC于点F(点F在点D的右侧),∠DAE=30°.
(1)、求证:四边形AFED是菱形;(2)、求证:AB2=BG•BC;(3)、若AB=AC , BG=CE , 联结AE , 求 的值.22. 已知在△ABC中,AB=AC= ,∠BAC=120°,△ADE的顶点D在边BC上,AE交BC于点F(点F在点D的右侧),∠DAE=30°. (1)、求证:△ABF∽△DCA;(2)、若AD=ED .
(1)、求证:△ABF∽△DCA;(2)、若AD=ED .①联结EC , 当点F是BC的黄金分割点(FC>BF)时,求 .
②联结BE , 当DF=1时,求BE的长.
23. 如图 (1)、如图1,Rt△ABC中,∠B=90°,AB=2BC,现以C为圆心、CB长为半径画弧交边AC于D,再以A为圆心、AD为半径画弧交边AB于E.求证: .(这个比值 叫做AE与AB的黄金比.)(2)、如果一等腰三角形的底边与腰的比等于黄金比,那么这个等腰三角形就叫做黄金三角形.请你以图2中的线段AB为腰,用直尺和圆规,作一个黄金三角形ABC.
(1)、如图1,Rt△ABC中,∠B=90°,AB=2BC,现以C为圆心、CB长为半径画弧交边AC于D,再以A为圆心、AD为半径画弧交边AB于E.求证: .(这个比值 叫做AE与AB的黄金比.)(2)、如果一等腰三角形的底边与腰的比等于黄金比,那么这个等腰三角形就叫做黄金三角形.请你以图2中的线段AB为腰,用直尺和圆规,作一个黄金三角形ABC.(注:直尺没有刻度!作图不要求写作法,但要求保留作图痕迹,并对作图中涉及到的点用字母进行标注)