鲁教版(五四学制)2022-2023学年八年级数学下册9.5 相似三角形判定定理的证明 同步测试
试卷更新日期:2023-03-12 类型:同步测试
一、单选题
-
1. 如图,在中,分别是、上的点, , 与相交于 , 则下列结论一定正确的是( )
 A、 B、 C、 D、2. 如图,在△ABC中,DE∥BC,若 , 则△ADE与△ABC的面积之比为( )
A、 B、 C、 D、2. 如图,在△ABC中,DE∥BC,若 , 则△ADE与△ABC的面积之比为( )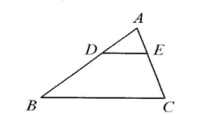 A、 B、 C、 D、3. 如图,已知直线l1∥l2∥l3 , 直线AB分别交三条平行线于点A、E、B,直线CD分别交三条平行线于点C、F、D,直线AB、CD相交于点O,若AE:EO:OB=4:2:7,则下列式子①;②;③;④中,正确的个数有( )
A、 B、 C、 D、3. 如图,已知直线l1∥l2∥l3 , 直线AB分别交三条平行线于点A、E、B,直线CD分别交三条平行线于点C、F、D,直线AB、CD相交于点O,若AE:EO:OB=4:2:7,则下列式子①;②;③;④中,正确的个数有( ) A、4个 B、3个 C、2个 D、1个4. 如图,在△ABC中,AB<AC,将△ABC以点A为旋转中心逆时针旋转得到△ADE,点D在BC边上,DE交AC于点F,则下列结论中错误的是( )
A、4个 B、3个 C、2个 D、1个4. 如图,在△ABC中,AB<AC,将△ABC以点A为旋转中心逆时针旋转得到△ADE,点D在BC边上,DE交AC于点F,则下列结论中错误的是( ) A、△AFE∽△DFC B、AD=AF C、DA平分∠BDE D、∠CDF=∠BAD5. 如图所示,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③;④AC2=AD•AB.其中单独能够判定△ABC∽△ACD的个数为( )
A、△AFE∽△DFC B、AD=AF C、DA平分∠BDE D、∠CDF=∠BAD5. 如图所示,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③;④AC2=AD•AB.其中单独能够判定△ABC∽△ACD的个数为( ) A、4 B、3 C、2 D、16. 如图,在△ABC中,AC=6,BC=8,∠C=90°,∠ABC与∠BAC的平分线交于点D,过点D作DE∥AC交AB于点E,则DE=( )
A、4 B、3 C、2 D、16. 如图,在△ABC中,AC=6,BC=8,∠C=90°,∠ABC与∠BAC的平分线交于点D,过点D作DE∥AC交AB于点E,则DE=( ) A、 B、2 C、 D、37. 如图,在中,D、E分别是边、上的点,且 , , .则下列说法不正确的是( )
A、 B、2 C、 D、37. 如图,在中,D、E分别是边、上的点,且 , , .则下列说法不正确的是( ) A、 B、 C、 D、8. 如图,与位似,点O为位似中心.已知 , 的周长为4,则的周长为( )
A、 B、 C、 D、8. 如图,与位似,点O为位似中心.已知 , 的周长为4,则的周长为( ) A、8 B、12 C、16 D、209. 如图,在正方形网格中:、的顶点都在正方形网格的格点上,则的度数为( )
A、8 B、12 C、16 D、209. 如图,在正方形网格中:、的顶点都在正方形网格的格点上,则的度数为( )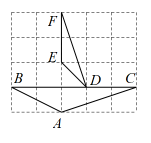 A、 B、 C、 D、10. 如图,在中,点D、E分别是、的中点,则下列四个结论,其中错误的结论是( )
A、 B、 C、 D、10. 如图,在中,点D、E分别是、的中点,则下列四个结论,其中错误的结论是( )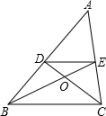 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在矩形中,点在上,连接 , 相交于点 , 若 , , 则的长为.
 12. 如图,在与中, , 连接、 , 若 , 则为.
12. 如图,在与中, , 连接、 , 若 , 则为. 13. 如图,在△ABC中,∠AED=∠B,若AB=10,AE=8,DE=6,则BC的长为.
13. 如图,在△ABC中,∠AED=∠B,若AB=10,AE=8,DE=6,则BC的长为. 14. 如图,在△ABC中,D、E分别是边AB、AC上的点,DE∥BC,AD:DB=1:2,S△ADE=1,则S四边形BCED的值为.
14. 如图,在△ABC中,D、E分别是边AB、AC上的点,DE∥BC,AD:DB=1:2,S△ADE=1,则S四边形BCED的值为. 15. 如图,在Rt△ABC中,∠BAC=90°,AB=3,BC=5,点P为BC边上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ长度的最小值为 .
15. 如图,在Rt△ABC中,∠BAC=90°,AB=3,BC=5,点P为BC边上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ长度的最小值为 .
三、解答题
-
16. 如图,在中, , D是边上一点,.求证.
 17. 如图,点D为边上一点,连接 , , , .
17. 如图,点D为边上一点,连接 , , , .求证:.
 18. 如图,在中,平分 , .若 , , , 求的长.
18. 如图,在中,平分 , .若 , , , 求的长.
四、综合题
-
19. 如图,在中,点分别在边上,连接.已知 , .
 (1)、求证:.(2)、若 , , 求的长.20. 如图,在正方形ABCD中,AB=4,P是BC边上一动点(不与B,C重合),DE⊥AP于E.
(1)、求证:.(2)、若 , , 求的长.20. 如图,在正方形ABCD中,AB=4,P是BC边上一动点(不与B,C重合),DE⊥AP于E. (1)、试说明△ADE∽△PAB;(2)、若PA=x,DE=y,请写出y与x之间的函数关系式.21. 如图,已知中, , , 点D、E在边上,.
(1)、试说明△ADE∽△PAB;(2)、若PA=x,DE=y,请写出y与x之间的函数关系式.21. 如图,已知中, , , 点D、E在边上,.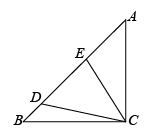 (1)、求证:;(2)、当 , 时,求的长.22. 如图,在△ABC中,点D在BC边上,点E在AC边上,且AD=AB,∠DEC=∠B.
(1)、求证:;(2)、当 , 时,求的长.22. 如图,在△ABC中,点D在BC边上,点E在AC边上,且AD=AB,∠DEC=∠B. (1)、求证:△AED∽△ADC;(2)、若AE=1,EC=3,求AB的长.23.
(1)、求证:△AED∽△ADC;(2)、若AE=1,EC=3,求AB的长.23. (1)、【问题提出】如图1,在中, , D是边上一点,F是边上一点,连接、 , .求证:;(2)、【问题探究】
(1)、【问题提出】如图1,在中, , D是边上一点,F是边上一点,连接、 , .求证:;(2)、【问题探究】如图2,在四边形中,点D是边的中点,连接、 , , 若 , 求线段的长;
(3)、【问题解决】某市进行绿化改造,美化生态环境.如图3,现有一块三角形的荒地计划改造公园,经测量米, , 按设计要求,要在三角形公园内建造一个以A为直角顶点的等腰直角三角形活动场所 , 且顶点D、顶点E分别在边、上,且米,请求出符合设计要求的等腰直角三角形活动场所的顶点D所在的位置(即的长).