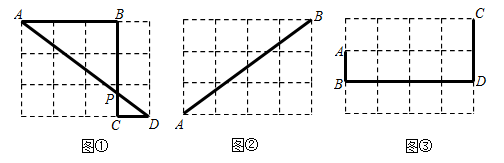
鲁教版（五四学制）2022-2023学年八年级数学下册9.4 探索三角形相似的条件同步测试

试卷更新日期：2023-03-12 类型：同步测试

进入出卷网下载

一、单选题

1. 如图所示，给出下列条件：①∠B＝∠ACD；②∠ADC＝∠ACB；③ $\frac{A C}{C D} = \frac{A B}{B C}$ ；④AC²＝AD•AB.其中单独能够判定△ABC∽△ACD的个数为（）

A、4 B、3 C、2 D、1

查看试题解析
2. 如图，点D在 $△ A B C$ 的边 $A C$ 上，添加一个条件，使得 $△ A D B ∽ △ A B C$ ，下列错误的是（）

A、 $A B^{2} = A D \cdot A C$ B、 $∠ A D B = ∠ A B C$ C、 $∠ A B D = ∠ C$ D、 $\frac{B D}{B C} = \frac{A D}{A B}$

查看试题解析
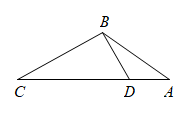3. 如图，将矩形ABCD沿着GE，EC，GF翻折，使得点A，B，D恰好都落在点O处，且点G，O，C在同一条直线上，点E，O，F 在另一条直线上. 以下结论正确的是（）

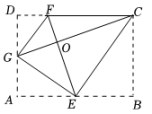A、△COF∽△CEG B、OC=3OF C、AB：AD=4：3 D、GE= $\sqrt{6}$ DF

查看试题解析
4. 如图，在四边形 $A B C D$ 中， $A D ∥ B C ， A C$ 与 $B D$ 相交于点O，则下列三角形中，与 $△ A O D$ 一定相似的是（）

A、 $△ B O C$ B、 $△ A O B$ C、 $△ D O C$ D、 $△ A B C$

查看试题解析
5. 如图，在 $△ A B C$ 中，点Р在边 $A B$ 上，则在下列四个条件中：① $∠ A C P = ∠ B$ ；② $∠ A P C = ∠ A C B$ ；③ $A C^{2} = A P \cdot A B$ ；④ $A B \cdot C P = A P \cdot C B$ ，能满足 $△ A P C$ 与 $△ A C B$ 相似的条件以及性质的是（）

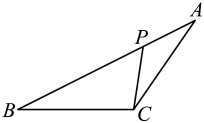A、①②④ B、①③④ C、②③④ D、①②③

查看试题解析
6. 如图，点P在 $△ A B C$ 的边AC上，要判断 $△ A B P ∽ △ A C B$ ，添加下列一个条件，不正确的是（）

A、 $∠ A B P = ∠ C$ B、 $∠ A P B = ∠ A B C$ C、 $\frac{A P}{A B} = \frac{A B}{A C}$ D、 $\frac{A P}{A B} = \frac{B P}{B C}$

查看试题解析
7. 如图，已知 $∠ 1 = ∠ 2$ ，那么添加下列一个条件后，仍无法判定 $△ A B C \sim △ A D E$ 的是（）

A、 $∠ C = ∠ E$ B、 $∠ B = ∠ A D E$ C、 $\frac{A B}{A D} = \frac{B C}{D E}$ D、 $\frac{A B}{A D} = \frac{A C}{A E}$

查看试题解析
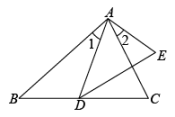8. 给出下列结论：
①任意两个等边三角形相似，②顶角对应相等的两个等腰三角形相似，③两条边对应成比例的两个直角三角形相似，其中正确的是（）

A、②③ B、①③ C、①② D、①②③

查看试题解析
9. 如图，点P在 $△ A B C$ 的边 $A C$ 上，添加如下一个条件后，仍不能得到 $△ A B P ∽ △ A C B$ 的是（）

A、 $\frac{A B}{B P} = \frac{A C}{C B}$ B、 $∠ A P B = ∠ A B C$ C、 $\frac{A P}{A B} = \frac{A B}{A C}$ D、 $∠ A B P = ∠ C$

查看试题解析
10. 已知在 $△ A B C$ 中， $∠ A = 78 ° ， A B = 4 ， A C = 6$ ，则下列选项中阴影部分的三角形与原 $△ A B C$ 不相似的是（　　）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 如图，在 $△ A B C$ 中， $A B > A C$ ，点D在 $A B$ 边上，点E在 $A C$ 边上且 $A D < A E$ .只需添加一个条件即可证明 $△ A B C ∽ △ A E D$ ，这个条件可以是（写出一个即可）.

查看试题解析
12. 如图，在 $△ A B C$ 中，点D，E分别为边 $A B$ ， $A C$ 上的点，试添加一个条件：，使得 $△ A D E$ 与 $△ A B C$ 相似．（任意写出一个满足条件的即可）

查看试题解析
13. 如图，已知矩形ABCD中，AB＝3，BC＝4，点M，N分别在边AD，BC上，沿着MN折叠矩形ABCD，使点A，B分别落在E，F处，且点F在线段CD上（不与两端点重合），过点M作MH⊥BC于点H，连接BF，给出下列判断：
①△MHN∽△BCF；

②折痕MN的长度的取值范围为3＜MN＜ $\frac{15}{4}$ ；

③当四边形CDMH为正方形时，N为HC的中点；

④若DF＝ $\frac{1}{3}$ DC，则折叠后重叠部分的面积为 $\frac{55}{12}$ ．

其中正确的是．（写出所有正确判断的序号）

查看试题解析
14. 如图，在 $△ A B C$ 中， $A C > A B$ ，过 $A B$ 上一点 D 作直线 $D F$ 交 $A C$ 于点 F，使所得的三角形与原三角形相似，这样的直线可以作出的条数为．

查看试题解析
15. 如图，在正方形网格中有三个三角形，分别是 $△ E B C$ ， $△ C D B$ ， $△ D E B$ ，其中与 $△ A B C$ 相似的是．

查看试题解析

三、解答题

16. 如图，点D为 $△ A B C$ 边 $A B$ 上一点，连接 $C D$ ， $A D = 2$ ， $B D = 6$ ， $A C = 4$ .
求证： $△ A C D ∽ △ A B C$ .

查看试题解析
17. 已知：如图，在 $R t △ A B C$ 中， $∠ B A C = 90 ° ， A D ⊥ B C$ 于D，E为直角边 $A C$ 的中点，过D，E作直线交 $A B$ 的延长线于F．求证： $△ D B F ∽ △ A D F$ ．

查看试题解析
18. 如图，在△ABP和△CDP中，∠B=∠C= $90 °$ ，点P在BC上，且∠APD= $90 °$ ，证明：△ABP $∽$ △PCD．

查看试题解析

四、综合题

19. 在四边形 $A B C D$ 中， $A C$ 为对角线， $A C = A B = B C$ ， $B E ⊥ A C$ 于点E， $C D = B E = \sqrt{3}$ ， $A D = 1$ ．

(1)、如图1，求证： $∠ A D C = 90 °$ ；

(2)、如图2，延长 $B E$ ，交 $A D$ 边的延长线于点F，交 $C D$ 边于点G，连接 $C F ， D E$ ，在不添加任何字母和辅助线的条件下，请直接写出图中与 $△ A B F$ 相似，但不全等的三角形．

查看试题解析
20. 如图，在△ABC中，D、E分别是边AC、BC的中点，F是BC延长线上一点，∠F＝∠B．

(1)、若AB＝10，求FD的长；

(2)、若AC＝BC，求证：△CDE∽△DFE．

查看试题解析
21. 如图，将一个 $R t △ B P E$ 与正方形 $A B C D$ 叠放在一起，并使其直角顶点P落在线段 $C D$ 上（不与C，D两点重合），斜边的一部分与线段 $A B$ 重合．

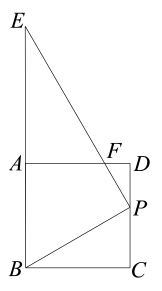(1)、图中与 $R t △ B C P$ 相似的三角形共有个，分别是；

(2)、请选择第（1）问答案中的任意一个三角形，完成该三角形与 $△ B C P$ 相似的证明．

查看试题解析
22. 以下各图均是由边长为1的小正方形组成的网格， $A 、 B 、 C 、 D$ 均在格点上．

(1)、在图①中， $\frac{P D}{P A}$ 的值为；

(2)、利用网格和无刻度的直尺作图，保留痕迹，不写作法．
①如图②，在 $A B$ 上找一点 $P$ ，使 $A P = 3$ ；
②如图③，在 $B D$ 上找一点 $P$ ，使 $Δ A P B$ $∽$ $Δ C P D$ ．

查看试题解析
23. 如图，在 $△$ ABC中，点D、E、F分别在AB、BC、AC边上，DE $∥$ AC，EF $∥$ AB.

(1)、求证： $△$ BDE∽ $△$ EFC.

(2)、若 $\frac{A F}{F C} = \frac{1}{2}$ ，AD＝6，求AB的长.

查看试题解析

鲁教版（五四学制）2022-2023学年八年级数学下册9.4 探索三角形相似的条件 同步测试

一、单选题

二、填空题

三、解答题

四、综合题

鲁教版（五四学制）2022-2023学年八年级数学下册9.4 探索三角形相似的条件同步测试