鲁教版（五四学制）2022-2023学年八年级数学下册9.3 相似多边形同步测试

试卷更新日期：2023-03-12 类型：同步测试

进入出卷网下载

一、单选题

1. 如图，E，F，G，H分别是矩形 $A B C D$ 四条边上的点，连接 $E F ， G H$ 相交于点I，且 $G H ∥ A D$ ， $E F ∥ A B$ ，矩形 $B F I G ∽$ 矩形 $E I H D$ ，连接 $A C$ 交 $G H ， E F$ 于点P，Q，下列一定能求出 $△ D P Q$ 面积的条件是（）

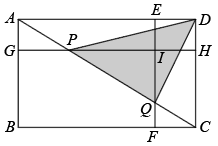A、矩形 $B F I G$ 和矩形 $E I H D$ 的面积之差 B、矩形 $A B C D$ 与矩形 $B F I G$ 的面积之差 C、矩形 $B F I G$ 和矩形 $F C H I$ 的面积之差 D、矩形 $B F I G$ 和矩形 $E I G A$ 的面积之差

查看试题解析
2. 如图，矩形ABCD∽矩形EFGH，已知 $A B = 3 cm$ ， $B C = 5 cm$ ， $E F = 6 cm$ ，则FG的长为（）

A、8cm B、10cm C、12cm D、15cm

查看试题解析
3. 若 $Δ A B C ∽ Δ A^{'} B^{'} C^{'}$ ，相似比为1：2，则 $Δ A B C$ 与 $Δ A^{'} B^{'} C^{'}$ 的面积的比为（）

A、1：2 B、2：1 C、1：4 D、4：1

查看试题解析
4. 如图， $E$ ， $F$ ， $G$ ， $H$ 是正方形 $A B C D$ 边上的点，且 $A G = B E = C H = D F$ ， $E F$ 和 $G H$ 将正方形剪切成四片进行重新拼接成四边形 $M Q P N$ ，若正方形 $A B C D$ 和四边形 $M Q P N$ 的面积之比为 $9 ： 10$ ，则 $A G ： G D =$ （）

A、2 B、3 C、 $\sqrt{2} + 1$ D、 $\sqrt{5}$

查看试题解析
5. 如图，已知四边形 $A B F E ∽$ 四边形 $E F C D$ ， $A B = 2$ ， $E F = 3$ ，则 $D C$ 的长是（）．

A、6 B、 $\frac{4}{3}$ C、 $\frac{9}{2}$ D、4

查看试题解析
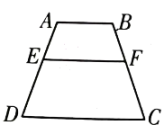6. 如图，点P是平行四边形 $A B C D$ 内部一点，过P分别作 $A B$ 和 $B C$ 的平行线交平行四边形 $A B C D$ 的四边于 $E ， F ， G ， H$ . 连结 $A C$ 分别交 $E G ， F H$ 于M和N. 若四边形 $F B G P ~$ 四边形 $E P H D$ ，且四边形 $F B C H$ 的面积是四边形 $A F P \overset{'}{E}$ 的3倍. 下列选项正确的是（　　）

A、 $E P = P H$ B、 $A N = E P$ C、 $A N = 2 M N$ D、 $A M = 2 C M$

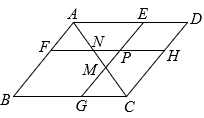查看试题解析
7. 如图，一块矩形ABCD绸布的长AB=a，宽AD=1，按照图中的方式将它裁成相同的三面矩形彩旗，如果裁出的每面彩旗与矩形ABCD绸布相似，则a的值等于（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、2 D、 $\sqrt{5}$

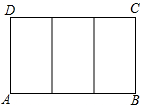查看试题解析
8. 两相似多边形的面积比是 $9 ： 16$ ，较小多边形的周长为 $18 c m$ ，则较大多边形的周长为（）

A、 $24 c m$ B、 $27 c m$ C、 $28 c m$ D、 $32 c m$

查看试题解析
9. 如图，四边形ABCD∽四边形EFGH，∠E＝85°，∠G＝90°，∠D＝120°，则∠B等于（）

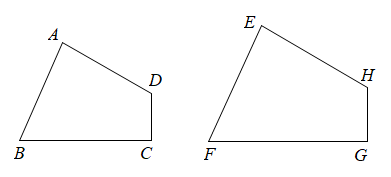A、55° B、65° C、75° D、85°

查看试题解析
10. 一个四边形的各边之比为1∶2∶3∶4，和它相似的另一个四边形的最小边长为 $5 c m$ ，则它的最大边长为（）

A、 $10 c m$ B、 $15 c m$ C、 $20 c m$ D、 $25 c m$

查看试题解析

二、填空题

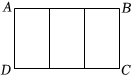
11. 若两个相似多边形的相似比是2：3，则它们的周长比是 .

查看试题解析
12. 如图，把一个大长方形 $A B C D$ 划分成三个全等的小长方形，若每一个小长方形均与大长方形 $A B C D$ 相似，则 $A D ： C D$ 的值为.

查看试题解析
13. 如图，四边形 $A B C D ∽$ 四边形 $A^{'} B^{'} C^{'} D^{'}$ ，若 $∠ B = 55 °$ ， $∠ C = 80 °$ ， $∠ A^{'} = 110 °$ ，则 $∠ D =$ °．

查看试题解析
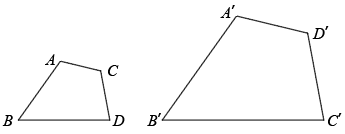14. 制作一块3m×2m长方形广告牌的成本是120元，在每平方米制作成本相同的情况下，若将此广告牌的四边都扩大为原来的3倍，那么扩大后长方形广告牌的成本是元．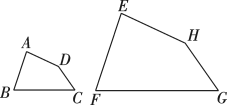

查看试题解析
15. 如图，四边形 $A B C D ∽$ 四边形 $E F G H$ ，若 $A B = 2$ ， $B C = 3$ ， $E F = 4$ ，则FG的长为．

查看试题解析

三、解答题

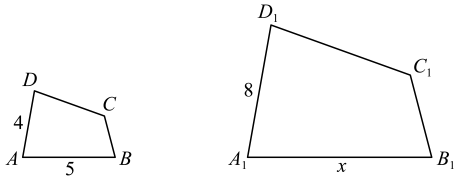
16. 如图，四边形ABCD∽四边形A₁B₁C₁D₁ ， ∠A＝80°，∠B＝75°，∠C＝125°，求x，∠D₁.

查看试题解析
17. 两个相似多边形的最长边分别为6cm和8cm，它们的周长之和为56cm，面积之差为28cm² ，求较小相似多边形的周长与面积.

查看试题解析
18. 如图，ABCD是边长为1的正方形，在它的左侧补一个矩形ABFE，使得新矩形CEFD与矩形ABEF相似，求BE的长．

查看试题解析

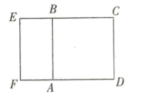
四、综合题

19. 如图，把一个矩形剪去一个边长和它的宽相等的正方形，若剩下的矩形与原矩形相似．

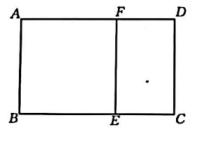(1)、求原矩形的长和宽的比．

(2)、若 $A B = 4$ ，求矩形 $A B C D$ 的面积．

查看试题解析
20. 如图是我国古代数学家赵爽创制的一副“勾股圆方图”(又称“赵爽弦图”)，它是由四个全等的直角三角形与中间的一个小正方形EFGH无缝拼成的大正方形ABCD.

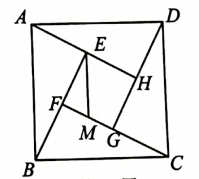(1)、若 $∠ A B E = 30^{°} ， E F = \sqrt{3} - 1$ ，求AB

(2)、点M在FG上， $A B / / E M$ ，且 $A B = 2 E M$ ，求正方形ABCD与正方形EFGH的周长比.

查看试题解析
21. 如图，四边形 $A B C D ∽$ 四边形 $A' B' C' D'$ .

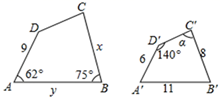(1)、 $α$ ＝，它们的相似比是.

(2)、求边x、y的长度.

查看试题解析
22. 一个矩形ABCD的较短边长为2．

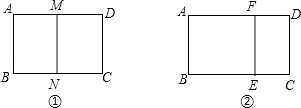(1)、如图①，若沿长边对折后得到的矩形与原矩形相似，求它的另一边长；

(2)、如图②，已知矩形ABCD的另一边长为4，剪去一个矩形ABEF后，余下的矩形EFDC与原矩形相似，求余下矩形EFDC的面积．

查看试题解析
23. 在矩形 $A B C D$ 中，点E是射线 $B C$ 上一动点，连接 $A E$ ，过点B作 $B F ⊥ A E$ 于点G，交直线 $C D$ 于点F.

(1)、当矩形 $A B C D$ 是正方形时，以点F为直角顶点在正方形 $A B C D$ 的外部作等腰直角三角形 $C F H$ ，连接 $E H$ .
①如图1，若点E在线段 $B C$ 上，则线段 $A E$ 与 $E H$ 之间的数量关系是_▲__，位置关系是_▲_；

②如图2，若点E在线段 $B C$ 的延长线上，①中的结论还成立吗？如果成立，请给予证明；如果不成立，请说明理由；

(2)、如图3，若点E在线段 $B C$ 上，以 $B E$ 和 $B F$ 为邻边作 $▱ B E H F$ ，M是 $B H$ 中点，连接 $G M$ ， $A B = 3$ ， $B C = 2$ ，求 $G M$ 的最小值.

查看试题解析

鲁教版（五四学制）2022-2023学年八年级数学下册9.3 相似多边形 同步测试

一、单选题

二、填空题

三、解答题

四、综合题

鲁教版（五四学制）2022-2023学年八年级数学下册9.3 相似多边形同步测试