冲刺2023中考——数学模拟考场仿真演练卷三
试卷更新日期:2023-03-12 类型:中考模拟
一、单选题(每题3分,共30分)
-
1. 下列各数是负数的是( )A、 B、 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 将直尺和三角板按如图所示的位置放置.若 , 则度数是( )
 A、 B、 C、 D、4. 定义新运算:对于任意实数 , 满足 , 其中等式右边是通常的加法、减法、乘法运算,例如 . 若(为实数)是关于的方程,则它的根的情况是( )A、有一个实数根 B、有两个不相等的实数根 C、有两个相等的实数根 D、没有实数根5. 将一枚飞镖任意投掷到如图所示的正六边形镖盘上,若飞镖落在镖盘上各点的机会相等,则飞镖落在阴影区域的概率为( )
A、 B、 C、 D、4. 定义新运算:对于任意实数 , 满足 , 其中等式右边是通常的加法、减法、乘法运算,例如 . 若(为实数)是关于的方程,则它的根的情况是( )A、有一个实数根 B、有两个不相等的实数根 C、有两个相等的实数根 D、没有实数根5. 将一枚飞镖任意投掷到如图所示的正六边形镖盘上,若飞镖落在镖盘上各点的机会相等,则飞镖落在阴影区域的概率为( )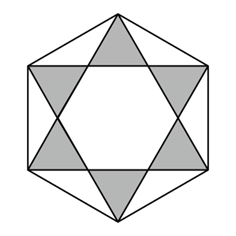 A、 B、 C、 D、6. 如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( )
A、 B、 C、 D、6. 如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( ) A、 B、 C、 D、7. 如图,矩形OABC与反比例函数(k1是非零常数,x>0)的图象交于点M,N,与反比例函数(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则k1-k2=( )
A、 B、 C、 D、7. 如图,矩形OABC与反比例函数(k1是非零常数,x>0)的图象交于点M,N,与反比例函数(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则k1-k2=( )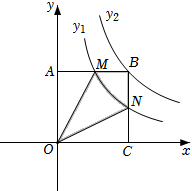 A、3 B、-3 C、 D、8. 如图.将扇形翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接 . 若 , 则图中阴影部分的面积是( )
A、3 B、-3 C、 D、8. 如图.将扇形翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接 . 若 , 则图中阴影部分的面积是( )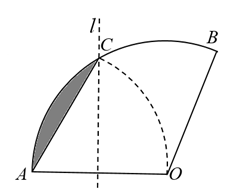 A、 B、 C、 D、9. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,OH=4,若菱形ABCD的面积为32 , 则CD的长为( )
A、 B、 C、 D、9. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,OH=4,若菱形ABCD的面积为32 , 则CD的长为( )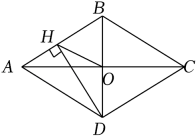 A、4 B、4 C、8 D、810. 如图,二次函数的图象关于直线对称,与x轴交于 , 两点,若 , 则下列四个结论:① , ② , ③ , ④ .
A、4 B、4 C、8 D、810. 如图,二次函数的图象关于直线对称,与x轴交于 , 两点,若 , 则下列四个结论:① , ② , ③ , ④ .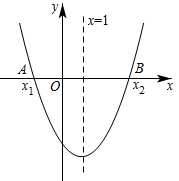
正确结论的个数为( )
A、1个 B、2个 C、3个 D、4个二、填空题(每空3分,共18分)
-
11. 今年是中国共青团建团100周年,据统计截止2021年12月31日,全国共有学生团员48310000名,48310000用科学记数法表示为 .12. 已知 , , 则的值为 .13. 关于x的不等式组 恰有3个整数解,则a的取值范围是.14. 一副三角板如图放置, , , , 则 .
 15. 如图,点的坐标是(0,3),将沿轴向右平移至 , 点的对应点E恰好落在直线上,则点移动的距离是 .
15. 如图,点的坐标是(0,3),将沿轴向右平移至 , 点的对应点E恰好落在直线上,则点移动的距离是 .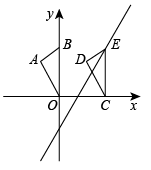 16. 如图,点O是正方形的中心, . 中,过点D,分别交于点G,M,连接 . 若 , 则的周长为 .
16. 如图,点O是正方形的中心, . 中,过点D,分别交于点G,M,连接 . 若 , 则的周长为 .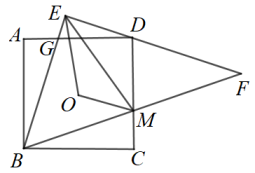
三、解答题(共7题,共72分)
-
17. 解答题(1)、计算: .(2)、先化简,再求值 , 其中 .(3)、求不等式组的整数解.18. 教育部在《大中小学劳动教育指导纲要(试行)》中明确要求:初中生每周课外生活和家庭生活中,劳动时间不少于3小时.某走读制初级中学为了解学生劳动时间的情况,对学生进行了随机抽样调查,并将调查结果制成不完整的统计图表,如图:
平均每周劳动时间的频数统计表
劳动时间小时
频数
t<3
9
3≤t<4
a
4≤t<5
66
t≥5
15

请根据图表信息,回答下列问题.
(1)、参加此次调查的总人数是人,频数统计表中a=;(2)、在扇形统计图中,D组所在扇形的圆心角度数是°;(3)、该校准备开展以“劳动美”为主题的教育活动,要从报名的2男2女中随机挑选2人在活动中分享劳动心得,请用树状图或列表法求恰好抽到一名男生和一名女生的概率.19. 如图,在Rt△ABC中,∠B=90°,AE平分∠BAC交BC于点E,O为AC上一点,经过点A、E的⊙O分别交AB、AC于点D、F,连接OD交AE于点M. (1)、求证:BC是⊙O的切线.(2)、若CF=2,sinC= , 求AE的长.20. 某数学兴趣小组自制测角仪到公园进行实地测量,活动过程如下:(1)、探究原理制作测角仪时,将细线一段固定在量角器圆心 处,另一端系小重物 .测量时,使支杆 、量角器90°刻度线 与铅垂线 相互重合(如图①),绕点 转动量角器,使观测目标 与直径两端点 共线(如图②),此目标 的仰角 .请说明两个角相等的理由.
(1)、求证:BC是⊙O的切线.(2)、若CF=2,sinC= , 求AE的长.20. 某数学兴趣小组自制测角仪到公园进行实地测量,活动过程如下:(1)、探究原理制作测角仪时,将细线一段固定在量角器圆心 处,另一端系小重物 .测量时,使支杆 、量角器90°刻度线 与铅垂线 相互重合(如图①),绕点 转动量角器,使观测目标 与直径两端点 共线(如图②),此目标 的仰角 .请说明两个角相等的理由.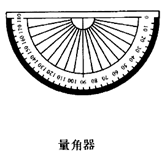
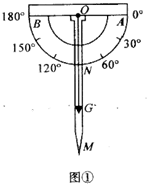
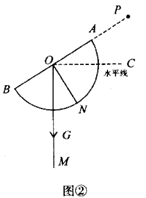 (2)、实地测量
(2)、实地测量如图③,公园广场上有一棵树,为了测量树高,同学们在观测点 处测得顶端 的仰角 ,观测点与树的距离 为5米,点 到地面的距离 为1.5米;求树高 . ( ,结果精确到0.1米)
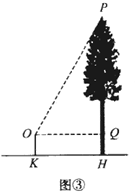 (3)、拓展探究
(3)、拓展探究公园高台上有一凉亭,为测量凉亭顶端 距离地面高度 (如图④),同学们讨论,决定先在水平地面上选取观测点 ( 在同一直线上),分别测得点 的仰角 ,再测得 间的距离 ,点 到地面的距离 均为1.5米;求 (用 表示).
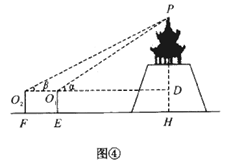 21. 阅读材料:
21. 阅读材料:材料1:若关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根为x1 , x2 , 则x1+x2= ,x1x2=
材料2:已知一元二次方程x2-x-1=0的两个实数根分别为m,n,求m2n+mn2的值.
解:∵一元二次方程x2-x-1=0的两个实数根分别为m,n,
∴m+n=1,mn=-1,
则m2n+mn2=mn(m+n)=-1×1=-1
根据上述材料,结合你所学的知识,完成下列问题:
(1)、材料理解:一元二次方程2x2-3x-1=0的两个根为x1 , x2 , 则x1+x2=;x1x2= .(2)、类比应用:已知一元二次方程2x2-3x-1=0的两根分别为m、n,求 的值.(3)、思维拓展:已知实数s、t满足2s2-3s-1=0,2t2-3t-1=0,且s≠t,求 的值.22. 如图1,在正方形ABCD中,E,F分别是BC,CD边上的点(点E不与点B,C重合),且 . (1)、当时,求证:;(2)、猜想BE,EF,DF三条线段之间存在的数量关系,并证明你的结论;(3)、如图2,连接AC,G是CB延长线上一点, , 垂足为K,交AC于点H且 . 若 , , 请用含a,b的代数式表示EF的长.23. 在平面直角坐标系中,抛物线y=﹣ +(m﹣1)x+2m与x轴交于A,B(4,0)两点,与y轴交于点C,点P是抛物线在第一象限内的一个动点.
(1)、当时,求证:;(2)、猜想BE,EF,DF三条线段之间存在的数量关系,并证明你的结论;(3)、如图2,连接AC,G是CB延长线上一点, , 垂足为K,交AC于点H且 . 若 , , 请用含a,b的代数式表示EF的长.23. 在平面直角坐标系中,抛物线y=﹣ +(m﹣1)x+2m与x轴交于A,B(4,0)两点,与y轴交于点C,点P是抛物线在第一象限内的一个动点.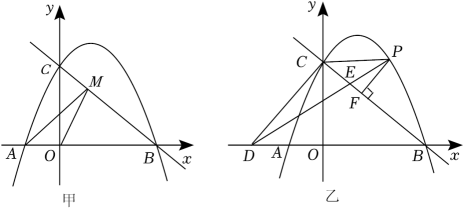 (1)、求抛物线的解析式,并直接写出点A,C的坐标;(2)、如图甲,点M是直线BC上的一个动点,连接AM,OM,是否存在点M使AM+OM最小,若存在,请求出点M的坐标,若不存在,请说明理由;(3)、如图乙,过点P作PF⊥BC,垂足为F,过点C作CD⊥BC,交x轴于点D,连接DP交BC于点E,连接CP.设△PEF的面积为S1 , △PEC的面积为S2 , 是否存在点P,使得最大,若存在,请求出点P的坐标,若不存在,请说明理由.
(1)、求抛物线的解析式,并直接写出点A,C的坐标;(2)、如图甲,点M是直线BC上的一个动点,连接AM,OM,是否存在点M使AM+OM最小,若存在,请求出点M的坐标,若不存在,请说明理由;(3)、如图乙,过点P作PF⊥BC,垂足为F,过点C作CD⊥BC,交x轴于点D,连接DP交BC于点E,连接CP.设△PEF的面积为S1 , △PEC的面积为S2 , 是否存在点P,使得最大,若存在,请求出点P的坐标,若不存在,请说明理由.