冲刺2023中考——数学模拟考场仿真演练卷二
试卷更新日期:2023-03-11 类型:中考模拟
一、单选题(每题3分,共30分)
-
1. -2的相反数是( )A、 B、-2 C、 D、22. 如图,l1∥l2 , ∠1=38°,∠2=46°,则∠3的度数为( )
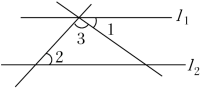 A、46° B、90° C、96° D、134°3. 如图,在中, , 的平分线交于点 , 为的中点,若 , 则的长是( )
A、46° B、90° C、96° D、134°3. 如图,在中, , 的平分线交于点 , 为的中点,若 , 则的长是( ) A、8 B、6 C、5 D、44. 下列计算正确的是( )A、2ab﹣ab=ab B、2ab+ab=2a2b2 C、4a3b2﹣2a=2a2b D、﹣2ab2﹣a2b=﹣3a2b25. 下面四幅图是我国一些博物馆的标志,其中既是轴对称图形又是中心对称图形的是( )A、温州博物馆
A、8 B、6 C、5 D、44. 下列计算正确的是( )A、2ab﹣ab=ab B、2ab+ab=2a2b2 C、4a3b2﹣2a=2a2b D、﹣2ab2﹣a2b=﹣3a2b25. 下面四幅图是我国一些博物馆的标志,其中既是轴对称图形又是中心对称图形的是( )A、温州博物馆 B、西藏博物馆
B、西藏博物馆 C、广东博物馆
C、广东博物馆 D、湖北博物馆
D、湖北博物馆 6. 如图,已知骰子相对两面的点数之和为7,下列图形为该骰子表面展开图的是( )
6. 如图,已知骰子相对两面的点数之和为7,下列图形为该骰子表面展开图的是( ) A、
A、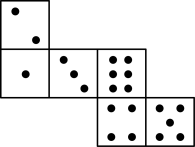 B、
B、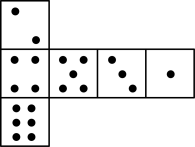 C、
C、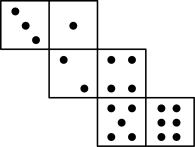 D、
D、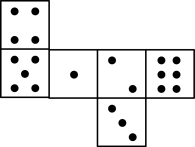 7. 受国际油价影响,今年我国汽油价格总体呈上升趋势.某地92号汽油价格三月底是6.2元/升,五月底是8.9元/升.设该地92号汽油价格这两个月平均每月的增长率为 , 根据题意列出方程,正确的是( )A、 B、 C、 D、8. 如图,正方形的对角线交于点O,点E是直线上一动点.若 , 则的最小值是( )
7. 受国际油价影响,今年我国汽油价格总体呈上升趋势.某地92号汽油价格三月底是6.2元/升,五月底是8.9元/升.设该地92号汽油价格这两个月平均每月的增长率为 , 根据题意列出方程,正确的是( )A、 B、 C、 D、8. 如图,正方形的对角线交于点O,点E是直线上一动点.若 , 则的最小值是( ) A、 B、 C、 D、9. 把量角器和含角的三角板按如图方式摆放:零刻度线与长直角边重合,移动量角器使外圆弧与斜边相切时,发现中心恰好在刻度处,短直角边过量角器外沿刻度处(即 , ).则阴影部分的面积为( )
A、 B、 C、 D、9. 把量角器和含角的三角板按如图方式摆放:零刻度线与长直角边重合,移动量角器使外圆弧与斜边相切时,发现中心恰好在刻度处,短直角边过量角器外沿刻度处(即 , ).则阴影部分的面积为( )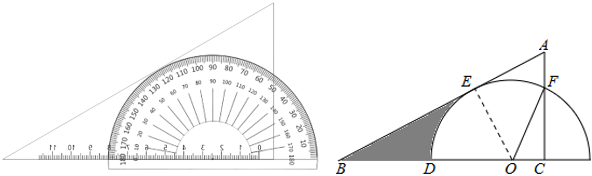 A、 B、 C、 D、10. 如图,二次函数的图象关于直线对称,与x轴交于 , 两点,若 , 则下列四个结论:① , ② , ③ , ④ .
A、 B、 C、 D、10. 如图,二次函数的图象关于直线对称,与x轴交于 , 两点,若 , 则下列四个结论:① , ② , ③ , ④ .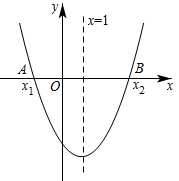
正确结论的个数为( )
A、1个 B、2个 C、3个 D、4个二、填空题(每空3分,共18分)
-
11. 若在实数范围内有意义,则实数x的取值范围是 .12. 已知 , , 则的值为 .13. 如图,直线 , 的边在直线上, , 将绕点顺时针旋转至 , 边交直线于点 , 则 .
 14. 化简分式:= .15. 如图,在△ABC中,边AB在x轴上,边AC交y轴于点E.反比例函数的图象恰好经过点C,与边BC交于点D.若AE=CE,CD=2BD, , 则k= .
14. 化简分式:= .15. 如图,在△ABC中,边AB在x轴上,边AC交y轴于点E.反比例函数的图象恰好经过点C,与边BC交于点D.若AE=CE,CD=2BD, , 则k= .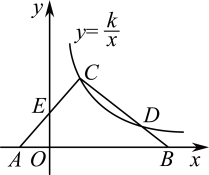 16. 已知二次函数 , 图象的一部分如图所示,该函数图象经过点 , 对称轴为直线.对于下列结论:①;②;③;④(其中);⑤若和均在该函数图象上,且 , 则.其中正确结论的个数共有个.
16. 已知二次函数 , 图象的一部分如图所示,该函数图象经过点 , 对称轴为直线.对于下列结论:①;②;③;④(其中);⑤若和均在该函数图象上,且 , 则.其中正确结论的个数共有个.
三、解答题(共9题,共72分)
-
17. 计算 .18. 先化简,再求值: , 从-3,-1,2中选择合适的a的值代入求值.19. 解不等式组并将其解集在数轴上表示出来.
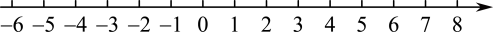 20. 2022年6月5日,“神舟十四号”载人航天飞船搭载“明星”机械臂成功发射.如图是处于工作状态的某型号手臂机器人示意图,是垂直于工作台的移动基座,、为机械臂,m,m,m, . 机械臂端点到工作台的距离m.
20. 2022年6月5日,“神舟十四号”载人航天飞船搭载“明星”机械臂成功发射.如图是处于工作状态的某型号手臂机器人示意图,是垂直于工作台的移动基座,、为机械臂,m,m,m, . 机械臂端点到工作台的距离m.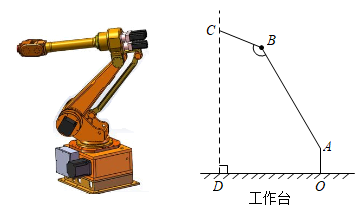 (1)、求、两点之间的距离;(2)、求长.(结果精确到0.1m,参考数据: , , , )21. 为扎实推进“五育并举”工作,某校利用课外活动时间开设了舞蹈、篮球、围棋和足球四个社团活动,每个学生只选择一项活动参加.为了解活动开展情况,学校随机抽取部分学生进行调查,将调查结果绘成如下表格和扇形统计图.
(1)、求、两点之间的距离;(2)、求长.(结果精确到0.1m,参考数据: , , , )21. 为扎实推进“五育并举”工作,某校利用课外活动时间开设了舞蹈、篮球、围棋和足球四个社团活动,每个学生只选择一项活动参加.为了解活动开展情况,学校随机抽取部分学生进行调查,将调查结果绘成如下表格和扇形统计图.参加四个社团活动人数统计表
社团活动
舞蹈
篮球
围棋
足球
人数
50
30
80
参加四个社团活动人数扇形统计图

请根据以上信息,回答下列问题:
(1)、抽取的学生共有人,其中参加围棋社的有人;(2)、若该校有3200人,估计全校参加篮球社的学生有多少人?(3)、某班有3男2女共5名学生参加足球社,现从中随机抽取2名学生参加学校足球队,请用树状图或列表法说明恰好抽到一男一女的概率.22. 如图,C,D是以AB为直径的半圆上的两点, , 连结BC,CD. (1)、求证: .(2)、若 , , 求阴影部分的面积.23. 如图,在平面直角坐标系中,直线与轴、轴分别交于点、两点,与双曲线交于点、两点, .
(1)、求证: .(2)、若 , , 求阴影部分的面积.23. 如图,在平面直角坐标系中,直线与轴、轴分别交于点、两点,与双曲线交于点、两点, .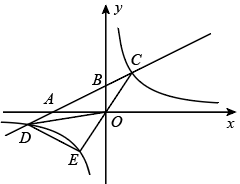 (1)、求 , 的值;(2)、求点坐标并直接写出不等式的解集;(3)、连接并延长交双曲线于点 , 连接、 , 求的面积.24. 如图,在菱形ABCD中,AB=5,BD为对角线.点E是边AB延长线上的任意一点,连结DE交BC于点F,BG平分∠CBE交DE于点G.
(1)、求 , 的值;(2)、求点坐标并直接写出不等式的解集;(3)、连接并延长交双曲线于点 , 连接、 , 求的面积.24. 如图,在菱形ABCD中,AB=5,BD为对角线.点E是边AB延长线上的任意一点,连结DE交BC于点F,BG平分∠CBE交DE于点G. (1)、求证:.(2)、若 .
(1)、求证:.(2)、若 .①求菱形的面积.
②求的值.
(3)、若 , 当的大小发生变化时(),在AE上找一点T,使GT为定值,说明理由并求出ET的值.25. 如图,二次函数的图象与x轴交于O(O为坐标原点),A两点,且二次函数的最小值为 , 点是其对称轴上一点,y轴上一点.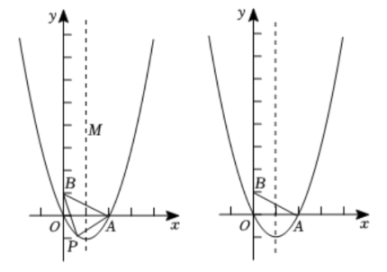 (1)、求二次函数的表达式;(2)、二次函数在第四象限的图象上有一点P,连结 , , 设点P的横坐标为t,的面积为S,求S与t的函数关系式;(3)、在二次函数图象上是否存在点N,使得以A、B、M、N为顶点的四边形是平行四边形?若存在,直接写出所有符合条件的点N的坐标,若不存在,请说明理由.
(1)、求二次函数的表达式;(2)、二次函数在第四象限的图象上有一点P,连结 , , 设点P的横坐标为t,的面积为S,求S与t的函数关系式;(3)、在二次函数图象上是否存在点N,使得以A、B、M、N为顶点的四边形是平行四边形?若存在,直接写出所有符合条件的点N的坐标,若不存在,请说明理由.