鲁教版（五四学制）2022-2023学年八年级数学下册8.3 用公式法解一元二次方程同步测试

试卷更新日期：2023-03-11 类型：同步测试

进入出卷网下载

一、单选题

1. 一元二次方程 $x^{2} - 2 x - 5 = 0$ 的两实数根之和等于（）

A、-2 B、2 C、-5 D、5

查看试题解析
2. 对于一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ ，满足 $a - b + c = 0$ ，且有两个相等的实数根，则（）

A、 $2 a - b = 0$ B、 $b = c$ C、 $2 a = c$ D、 $b + c = 0$

查看试题解析
3. 若一元二次方程 $a x^{2} - x + 2 = 0$ 有两个不相等的实数根，则实数a的取值范围为（）

A、 $a < \frac{1}{8}$ B、 $a < \frac{1}{8}$ 且 $a \neq 0$ C、 $a \leq \frac{1}{8}$ 且 $a \neq 0$ D、 $a > \frac{1}{8}$

查看试题解析
4. 在Rt△ABC中，∠C＝90°，a，b，c分别是∠A，∠B，∠C的对边，a，b是关于x的方程x²－7x＋c＋7＝0的两根，那么AB边上的中线长是（　　）

A、 $\frac{3}{2}$ B、 $\frac{5}{2}$ C、5 D、2

查看试题解析
5. 若 $x_{1} ， x_{2}$ 是一元二次方程 $x^{2} - 3 x - 10 = 0$ 的两个根.则 $x_{1} \cdot x_{2}$ 的值为（）

A、3 B、10 C、 $- 3$ D、 $- 10$

查看试题解析
6. 关于x的一元二次方程 $x^{2} - 4 x + 1 = 2 k$ 有两个不相等的实数根，则k的取值范围为（）

A、 $k > \frac{3}{2}$ B、 $k > 1$ C、 $k < 1$ D、 $k > - \frac{3}{2}$

查看试题解析
7. 已知 $α$ 、 $β$ 是方程 $x^{2} - 2 x - 2022 = 0$ 的两个实数根，则 $α^{2} - 4 α - 2 β - 2$ 的值是（）

A、2016 B、2018 C、2022 D、2024

查看试题解析
8. 若关于x的一元二次方程 $x^{2} - 4 x + m = 0$ 没有实数根，点 $A (x_{1} ， y_{1})$ 、 $B (x_{2} ， y_{2})$ 是反比例函数 $y = \frac{m}{x}$ 的图象上的两个点，若x₁<x₂<0，则y₁、y₂的大小关系为（）

A、y₁>y₂ B、y₁<y₂ C、y₁=y₂ D、不能确定

查看试题解析
9. 已知关于 $x$ 的一元二次方程 $x^{2} + 3 x - 2 = 0$ ，下列说法正确的是（）

A、方程有两个相等的实数根 B、方程有两个不相等的实数根 C、方程没有实数根 D、方程的根为 $x_{1} = 1$ ， $x_{2} = - 2$

查看试题解析
10. 已知关于x的一元二次方程 $(k + 1) x^{2} - 2 x + 1 = 0$ 有两个不相等的实数根，则k的取值范围为（）

A、 $k \geq 0$ B、 $k \leq 0$ 且 $k \neq - 1$ C、 $k < 0$ 且 $k \neq - 1$ D、 $k < 0$

查看试题解析

二、填空题

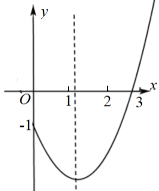
11. 关于x的一元二次方程x²+mx-3＝0的一个根是1，则另一根为.

查看试题解析
12. 已知关于 $x$ 的一元二次方程 $x^{2} + (2 m + 1) x + m - 2 = 0$ 有两个实数根 $x_{1}$ 、 $x_{2}$ ，且 $x_{1} + x_{2} + x_{1} x_{2} = 1$ ，则 $m =$ .

查看试题解析
13. 二次函数 $y = a x^{2} + b x + c$ 图像的一部分如图所示，下列结论：① $a b > 0$ ；② $a - b + c < 0$ ；③ $a x^{2} + b x + c + 1 = 0$ 有两个相等的实数根；④ $- 4 a < b < - 2 a$ .其中正确的为（只填序号）.

查看试题解析
14. 已知关于x的方程x²－2x＋2k－1＝0的两根分别是x₁、x₂ ，且 $\frac{x_{2}}{x_{1}} + \frac{x_{1}}{x_{2}} =$ x₁·x₂ ，则k的值是．

查看试题解析
15. 若一元二次方程 $x^{2} + m x + 2 = 0$ 有两个相等的实数根，则 $m$ 的值是.

查看试题解析

三、解答题

16. 已知 $x_{1}$ 、 $x_{2}$ 是一元二次方程 $x^{2} - 3 x - 2 = 0$ 的两个根，求 $2 x_{1} x_{2} - x_{1} - x_{2}$ 的值.

查看试题解析
17. 已知矩形ABCD两邻边AB、BC的长是关于x的方程 $x^{2} - 2 m x + 4 m - 4 = 0$ 的两个实数根.当m为何值时，矩形ABCD的两邻边AB、BC的长相等.

查看试题解析
18. 已知关于x的方程 $x^{2} - 2 x + m - 2 = 0$ 有两个实数根 $x_{1}$ ， $x_{2}$ ，求 $m$ 的取值范围.

查看试题解析

四、综合题

19. 已知：关于x的一元二次方程 $x^{2} - 2 m x + m^{2} - 1 = 0$ .

(1)、判断方程的根的情况；

(2)、若 $△ A B C$ 为等腰三角形， $A B = 5 c m$ ，另外两条边长是该方程的根，求 $△ A B C$ 的周长.

查看试题解析
20. 已知关于x的一元二次方程 $x^{2} + 2 x + 2 m - 3 = 0$ 有两个不相等的实数根.

(1)、求m的取值范围；

(2)、若m为正整数，求此时方程的根.

查看试题解析
21. 若关于x的方程 $x^{2} - 2 x + k - 1 = 0$ 有两个不相等的实数根.

(1)、求k的取值范围；

(2)、设方程的两根分别是 $x_{1}$ 、 $x_{2}$ ，且满足 $\frac{x_{2}}{x_{1}} + \frac{x_{1}}{x_{2}} = x_{1} x_{2}$ ，求 $k$ 的值.

查看试题解析
22. 已知关于 $x$ 的方程 $x^{2} - 2 m x + m^{2} - 9 = 0$ ．

(1)、求证：方程有两个不相等的实数根；

(2)、设此方程的两个根分别为 $x_{1}$ ， $x_{2}$ ，且 $x_{1} > x_{2}$ ，若 $2 x_{1} = x_{2} + 5$ ，求 $m$ 的值．

查看试题解析
23. 阅读材料，解答问题：已知实数m，n满足 $m^{2} - m - 1 = 0$ ， $n^{2} - n - 1 = 0$ ，且 $m \neq n$ ，则m，n是方程 $x^{2} - x - 1 = 0$ 的两个不相等的实数根，由韦达定理可知 $m + n = 1$ ， $m n = - 1$ .根据上述材料，解决以下问题：

(1)、直接应用：已知实数a，b满足： $a^{2} - 7 a + 1 = 0$ ， $b^{2} - 7 b + 1 = 0$ 且 $a \neq b$ ，则 $a + b =$ ， $a b =$ ；

(2)、间接应用：在（1）条件下，求 $\frac{1}{\sqrt{a}} + \frac{1}{\sqrt{b}}$ 的值；

(3)、拓展应用：已知实数x，y满足： $\frac{1}{m^{2}} + \frac{1}{m} = 7$ ， $n^{2} - n = 7$ 且 $m n \neq - 1$ ，求 $\frac{1}{m^{2}} + n^{2}$ 的值.

查看试题解析

鲁教版（五四学制）2022-2023学年八年级数学下册8.3 用公式法解一元二次方程 同步测试

一、单选题

二、填空题

三、解答题

四、综合题

鲁教版（五四学制）2022-2023学年八年级数学下册8.3 用公式法解一元二次方程同步测试