鲁教版(五四学制)2022-2023学年七年级数学下册11.6 一元一次不等式组 同步测试
试卷更新日期:2023-03-11 类型:同步测试
一、单选题
-
1. 关于x的不等式组恰好有3个整数解,则a满足( )A、 B、 C、 D、2. 若不等式组的解集是x<2,则m的取值范围是( )A、m=2 B、m≥2 C、m<2 D、m>23. 如图是测量一颗玻璃球体积的过程:

(1)将的水倒进一个容量为的杯子中;
(2)将五颗相同的玻璃球放入水中,结果水没有满;
(3)再加一颗同样的玻璃球放入水中,结果水满溢出.根据以上过程,推测这样一颗玻璃球的体积范围是( )
A、以上,以下 B、以上,以下 C、以上,以下 D、以上,以下4. 不等式组的解集在数轴上用阴影表示正确的是( )A、 B、
B、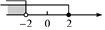 C、
C、 D、
D、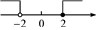 5. 如果关于的不等式组的解集为 , 且关于的分式方程有非负数解,则所有符合条件的整数的值之和是( )A、-2 B、0 C、3 D、56. 若关于x的不等式组有解,且关于x的分式方程的解为非负数,则满足条件的整数a的值的和为( )A、-3 B、-4 C、-5 D、-67. 不等式组的解集是( )A、 B、 C、或 D、8. 若不等式组有解,则a的取值范围是( )A、 B、 C、 D、9. 不等式组的最小整数解为( )A、 B、 C、 D、10. 若关于x的不等式组只有4个整数解,则a的取值范围是( )A、 B、 C、 D、
5. 如果关于的不等式组的解集为 , 且关于的分式方程有非负数解,则所有符合条件的整数的值之和是( )A、-2 B、0 C、3 D、56. 若关于x的不等式组有解,且关于x的分式方程的解为非负数,则满足条件的整数a的值的和为( )A、-3 B、-4 C、-5 D、-67. 不等式组的解集是( )A、 B、 C、或 D、8. 若不等式组有解,则a的取值范围是( )A、 B、 C、 D、9. 不等式组的最小整数解为( )A、 B、 C、 D、10. 若关于x的不等式组只有4个整数解,则a的取值范围是( )A、 B、 C、 D、二、填空题
-
11. 若关于x的不等式组有3个整数解,则m的取值范围是 .12. 定义:对于实数a,符号表示不大于a的最大整数.例如: , , .如果 , 则满足条件的所有正整数x的值是.13. 运行程序如图所示,规定:从“输入一个值”到“结果是否”为一次程序操作,如果程序操作进行了三次才停止,那么的取值范围是.
 14. 要使方程组有正整数解,则整数a有个.15. 我们用表示不小于a的最小整数,例如: , , .若 , 则x的取值范围是.
14. 要使方程组有正整数解,则整数a有个.15. 我们用表示不小于a的最小整数,例如: , , .若 , 则x的取值范围是.三、解答题
-
16. 求不等式组的最大整数解.17. 解一元一次不等式组 , 并把解表示在数轴上.
 18. 已知关于x、y的方程组的解x,y都是正数,求m的取值范围.
18. 已知关于x、y的方程组的解x,y都是正数,求m的取值范围.四、综合题
-
19.(1)、解不等式;(2)、解不等式组: , 并把它的解集在数轴上表示出来.
 20. 某社区为了更好地开展“垃圾分类,美丽永州”活动,需购买A,B两种类型垃圾桶,用1600元可购进A型垃圾桶14个和B型垃圾桶8个,且购买3个A型垃圾桶的费用与购买4个B型垃圾桶的费用相同,请解答下列问题:(1)、求出A型垃圾桶和B型垃圾桶的单价.(2)、若社区欲用不超过3600元购进两种垃圾桶共50个,其中A型垃圾桶至少29个,求有哪几种购买方案?21. 某体育馆计划从一家体育用品商店一次性购买若干个气排球和篮球(每个气排球的价格都相同,每个篮球的价格都相同).经洽谈,购买1个气排球和2个篮球共需210元;购买2个气排球和3个篮球共需340元.(1)、每个气排球和每个篮球的价格各是多少元?(2)、该体育馆决定从这家体育用品商店一次性购买气排球和篮球共50个,总费用不超过3200元,且购买气排球的个数少于30个,有哪几种购买方案?22. 某单位为做好防疫物资调配发放工作,租用A、B两种型号的车给全市各个防疫点配送消毒液。已知用2辆A型车和1辆B型车装满货物一次可运货7吨;用1辆A型车和2辆B型车装满货物一次可运货8吨。现有15吨消毒液需要配送,计划租用A、B两种型号车6辆一次配送完消毒液,其中A车至少租用1辆根据以上信息,解答下列问题:(1)、1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?(2)、请你帮助该单位设计一次配送完15吨消毒液的租车方案;23. 在数轴上,点O表示的数为0,点M表示的数为m().给出如下定义:对于该数轴上的一点P与线段上一点Q,如果线段的长度有最大值,那么称这个最大值为点P与线段的“闭距离”,如图1,若 , 点P表示的数为3,当点Q与点M重合时,线段的长最大,值是4,则点P与线段的“闭距离”为4.
20. 某社区为了更好地开展“垃圾分类,美丽永州”活动,需购买A,B两种类型垃圾桶,用1600元可购进A型垃圾桶14个和B型垃圾桶8个,且购买3个A型垃圾桶的费用与购买4个B型垃圾桶的费用相同,请解答下列问题:(1)、求出A型垃圾桶和B型垃圾桶的单价.(2)、若社区欲用不超过3600元购进两种垃圾桶共50个,其中A型垃圾桶至少29个,求有哪几种购买方案?21. 某体育馆计划从一家体育用品商店一次性购买若干个气排球和篮球(每个气排球的价格都相同,每个篮球的价格都相同).经洽谈,购买1个气排球和2个篮球共需210元;购买2个气排球和3个篮球共需340元.(1)、每个气排球和每个篮球的价格各是多少元?(2)、该体育馆决定从这家体育用品商店一次性购买气排球和篮球共50个,总费用不超过3200元,且购买气排球的个数少于30个,有哪几种购买方案?22. 某单位为做好防疫物资调配发放工作,租用A、B两种型号的车给全市各个防疫点配送消毒液。已知用2辆A型车和1辆B型车装满货物一次可运货7吨;用1辆A型车和2辆B型车装满货物一次可运货8吨。现有15吨消毒液需要配送,计划租用A、B两种型号车6辆一次配送完消毒液,其中A车至少租用1辆根据以上信息,解答下列问题:(1)、1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?(2)、请你帮助该单位设计一次配送完15吨消毒液的租车方案;23. 在数轴上,点O表示的数为0,点M表示的数为m().给出如下定义:对于该数轴上的一点P与线段上一点Q,如果线段的长度有最大值,那么称这个最大值为点P与线段的“闭距离”,如图1,若 , 点P表示的数为3,当点Q与点M重合时,线段的长最大,值是4,则点P与线段的“闭距离”为4.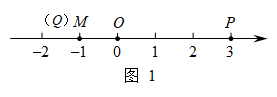 (1)、如图2,在该数轴上,点A表示的数为 , 点B表示的数为2.
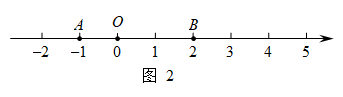
(1)、如图2,在该数轴上,点A表示的数为 , 点B表示的数为2.①当时,点A与线段的“闭距离”为 ▲ ;
②若点B与线段的“闭距离”为3,求m的值;
 (2)、在该数轴上,点C表示的数为 , 点D表示的数为 , 若线段上存在点G,使得点G与线段的“闭距离”为4,直接写出m的最大值与最小值.
(2)、在该数轴上,点C表示的数为 , 点D表示的数为 , 若线段上存在点G,使得点G与线段的“闭距离”为4,直接写出m的最大值与最小值.