鲁教版(五四学制)2022-2023学年七年级数学下册11.5 一元一次不等式与一次函数 同步测试
试卷更新日期:2023-03-11 类型:同步测试
一、单选题
-
1. 如图,直线与直线交于点 , 则不等式的解集是( )
 A、 B、 C、 D、2. 如图,直线y=x+m与y=nx-5n(n≠0)的交点的横坐标为3,则关于x的不等式x+m>nx-5n>0的整数解为( )
A、 B、 C、 D、2. 如图,直线y=x+m与y=nx-5n(n≠0)的交点的横坐标为3,则关于x的不等式x+m>nx-5n>0的整数解为( )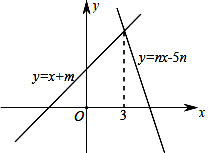 A、6 B、5 C、4 D、33. 如图所示,一次函数是常数,与正比例函数是常数,的图象相交于点 , 下列判断错误的是( )
A、6 B、5 C、4 D、33. 如图所示,一次函数是常数,与正比例函数是常数,的图象相交于点 , 下列判断错误的是( ) A、关于的方程的解是 B、关于的不等式的解集是 C、当时,函数的值比函数的值大 D、关于 , 的方程组 的解是4. 如图所示,一次函数(k,b是常数)与正比例函数(m是常数,)的图像相交于点 , 下列判断错误的是( )
A、关于的方程的解是 B、关于的不等式的解集是 C、当时,函数的值比函数的值大 D、关于 , 的方程组 的解是4. 如图所示,一次函数(k,b是常数)与正比例函数(m是常数,)的图像相交于点 , 下列判断错误的是( )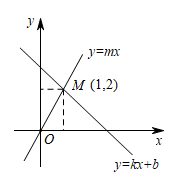 A、关于x的方程的解是 B、关于x的不等式的解集是 C、当时,函数的值比函数的值大 D、关于x,y的方程组的解是5. 如图,一次函数与一次函数的图象交于点P(1,3),则关于x的不等式的解集是( )
A、关于x的方程的解是 B、关于x的不等式的解集是 C、当时,函数的值比函数的值大 D、关于x,y的方程组的解是5. 如图,一次函数与一次函数的图象交于点P(1,3),则关于x的不等式的解集是( ) A、 B、 C、 D、6. 直线:与直线:在同一平面直角坐标系中的图象如图所示,则关于的不等式的解集为( )
A、 B、 C、 D、6. 直线:与直线:在同一平面直角坐标系中的图象如图所示,则关于的不等式的解集为( ) A、 B、 C、 D、7. 如图,函数和的图象相交于点 , 则不等式的解集为( )
A、 B、 C、 D、7. 如图,函数和的图象相交于点 , 则不等式的解集为( ) A、 B、 C、 D、8. 如图,函数和的图象相交于点 , 则不等式的解集为( )
A、 B、 C、 D、8. 如图,函数和的图象相交于点 , 则不等式的解集为( )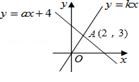 A、 B、 C、 D、9. 将直线向上平移3个单位长度后得到直线 , 下列关于直线的说法正确的是( )A、随的增大而减小 B、与轴交于点 C、经过第二、三、四象限 D、若关于的不等式 , 则10. 如图,一次函数的图象经过点和点 , 一次函数的图象过点 , 则不等式的解集为( )
A、 B、 C、 D、9. 将直线向上平移3个单位长度后得到直线 , 下列关于直线的说法正确的是( )A、随的增大而减小 B、与轴交于点 C、经过第二、三、四象限 D、若关于的不等式 , 则10. 如图,一次函数的图象经过点和点 , 一次函数的图象过点 , 则不等式的解集为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知过点的直线不经过第一象限.s=a+2b,则s的取值范围是.12. 如图,函数y=2x和y=ax+2的图象相交于点A(m,4),则不等式2x<ax+2的解集为.
 13. 如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式ax-3<3x+b≤0的解集是.
13. 如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式ax-3<3x+b≤0的解集是. 14. 若一次函数y=kx+b的图象如图所示,则关于kx+b>0的不等式的解集为 .
14. 若一次函数y=kx+b的图象如图所示,则关于kx+b>0的不等式的解集为 . 15. 如图,在平面直角坐标系中,直线:经过点 , 则关于的不等式的解集为 .
15. 如图,在平面直角坐标系中,直线:经过点 , 则关于的不等式的解集为 .
三、解答题
-
16. 由于灯管老化,现某学校要购进A、B两种节能灯管320只,A、B两种灯管的单价分别为25元和30元,现要求B种灯管的数量不少于A种灯管的3倍,那么购买A种灯管多少只时,可使所付金额最少?最少为多少元?17. 在给出的网格中画出一次函数 的图象,并结合图象求:

①方程 的解;
②不等式 的解集;
③不等式 的解集.
18. 已知一次函数 ,当 时, ,求此一次函数的表达式.四、综合题
-
19. 2022年北京承办了第24届冬季奥林匹克运动会,某商店为了抓住冬奥会的商机,决定购买A,B两种冬奥会纪念品,若购进A种纪念品20件,B种纪念品10件,需要2000元.若购进A种纪念品10件,B种纪念品8件,需要1150元.(1)、求购进A,B两种纪念品每件各需多少元?(2)、若该商店购进这两种纪念品共1000件,总费用不超过60000元,销售每件A种纪念品可获利润30元,每件B种纪念品可获利润20元.设购进A种纪念品a件,请求出总利润最高时的进货方案.20. 如图,直线y=kx+b经过点A(-5,0),B(-1,4).
 (1)、求直线AB的表达式;(2)、若直线y=-2x-4与直线AB相交于点C,求点C的坐标;(3)、根据图象,写出关于x的不等式kx+b>-2x-4的解集.21. 在直角坐标系内,已知直线 , 请画出直线 , 并由图象解答:
(1)、求直线AB的表达式;(2)、若直线y=-2x-4与直线AB相交于点C,求点C的坐标;(3)、根据图象,写出关于x的不等式kx+b>-2x-4的解集.21. 在直角坐标系内,已知直线 , 请画出直线 , 并由图象解答: (1)、写出方程组的解;(2)、写出不等式的解集.22. 在“新冠病毒”防控期间,某益康医疗器械公司分两次购进酒精消毒液与测温枪两种商品进行销售两次购进同一商品的进价相同,具体情况如表所示:
(1)、写出方程组的解;(2)、写出不等式的解集.22. 在“新冠病毒”防控期间,某益康医疗器械公司分两次购进酒精消毒液与测温枪两种商品进行销售两次购进同一商品的进价相同,具体情况如表所示:项目
购进数量(件)
购进所需费用(元)
酒精消毒液
测温枪
第一次
30
40
7560
第二次
40
30
5880
(1)、求酒精消毒液和测温枪两种商品每件的进价分别是多少元?(2)、公司决定酒精消毒液以每件20元出售,测温枪以每件240元出售.为满足市场需求,需购进这两种商品共1000件,且酒精消毒液的数量不少于测温枪数量的4倍,求该公司销售完上述1000件商品获得的最大利润.23. 如图,直线与x轴交于点 , 与直线交于点 , 直线交y轴于点B,直线交x轴于点C.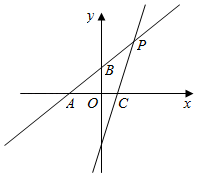 (1)、求直线的表达式;(2)、请直接写出使得不等式成立的x的取值范围.(3)、在直线上找点M,使得 , 求点M的坐标.
(1)、求直线的表达式;(2)、请直接写出使得不等式成立的x的取值范围.(3)、在直线上找点M,使得 , 求点M的坐标.