鲁教版(五四学制)2022-2023学年七年级数学下册11.3 不等式的解集 同步测试
试卷更新日期:2023-03-11 类型:同步测试
一、单选题
-
1. 如图所示,在数轴上表示不等式正确的是( )
 A、 B、 C、 D、2. 不等式组的解集在数轴上用阴影表示正确的是( )A、
A、 B、 C、 D、2. 不等式组的解集在数轴上用阴影表示正确的是( )A、 B、
B、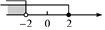 C、
C、 D、
D、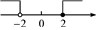 3. 不等式组的解集在数轴上表示正确的是( )A、
3. 不等式组的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 4. 若不等式组的解集为 , 则的值是( )A、-3 B、-2 C、-1 D、05. 下列不等式组的解集,在数轴上表示为如图所示的是( )
4. 若不等式组的解集为 , 则的值是( )A、-3 B、-2 C、-1 D、05. 下列不等式组的解集,在数轴上表示为如图所示的是( ) A、 B、 C、 D、或6. 关于x的不等式的解如图所示,则a的值是( )
A、 B、 C、 D、或6. 关于x的不等式的解如图所示,则a的值是( ) A、3 B、0 C、﹣6 D、-37. 若a,b,c,d为整数,且a<2b,b<3c,c<4d,d<100,则a可能取的最大值是( )A、2367 B、2375 C、2391 D、23998. 如图所示,在数轴上表示了某不等式的解集,则这个不等式可能是( )
A、3 B、0 C、﹣6 D、-37. 若a,b,c,d为整数,且a<2b,b<3c,c<4d,d<100,则a可能取的最大值是( )A、2367 B、2375 C、2391 D、23998. 如图所示,在数轴上表示了某不等式的解集,则这个不等式可能是( ) A、x≤1 B、x≤-1 C、x≥1 D、x≥-19. 如图,是关于x的不等式2x-m< -1的解集,则整数m的值为( )
A、x≤1 B、x≤-1 C、x≥1 D、x≥-19. 如图,是关于x的不等式2x-m< -1的解集,则整数m的值为( ) A、 B、 C、 D、10. 若不等式组的解集为x>4,则a的取值范围是( )A、a>4 B、a<4 C、a≤4 D、a≥4
A、 B、 C、 D、10. 若不等式组的解集为x>4,则a的取值范围是( )A、a>4 B、a<4 C、a≤4 D、a≥4二、填空题
-
11. 若数使关于的分式方程的解为正数,且使关于的不等式组的解集为 , 则符合条件所有整数的积为 .12. 如图,数轴上A,B两点表示的数分别为a,b,则关于x的不等式组的解集是 .
 13. 不等式的解集是.14. 在实数范围内规定新运算“”,其规则是: , 例如:已知不等式的解集在数轴上如图所示,则的值是 .
13. 不等式的解集是.14. 在实数范围内规定新运算“”,其规则是: , 例如:已知不等式的解集在数轴上如图所示,则的值是 .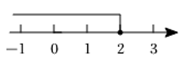 15. 已知不等式组的解集是 , 则关于的方程的解为.
15. 已知不等式组的解集是 , 则关于的方程的解为.三、解答题
-
16. 解一元一次不等式组 , 并把解表示在数轴上.
 17. 解不等式: , 并把解集表示在数轴上.18. 解不等式组 , 并把解集表示在数轴上.
17. 解不等式: , 并把解集表示在数轴上.18. 解不等式组 , 并把解集表示在数轴上.
四、综合题
-
19.(1)、解不等式;(2)、解不等式组: , 并把它的解集在数轴上表示出来.
 20. 解不等式,并将解集在数轴上表示出来.(1)、;(2)、.21.(1)、解不等式组: , 并把解表示在数轴上:
20. 解不等式,并将解集在数轴上表示出来.(1)、;(2)、.21.(1)、解不等式组: , 并把解表示在数轴上: (2)、写出(1)中不等式组的所有整数解.
(2)、写出(1)中不等式组的所有整数解.

