鲁教版(五四学制)2022-2023学年七年级数学下册10.4 线段的垂直平分线 同步测试
试卷更新日期:2023-03-11 类型:同步测试
一、单选题
-
1. 如图,△ABC中,AB<AC<BC,如果要使用尺规作图的方法在BC上确定一点P,使PA+PB=BC,那么符合要求的作图痕迹是( )A、
 B、
B、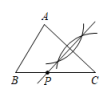 C、
C、 D、
D、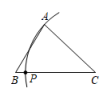 2. 如图,已知.
2. 如图,已知.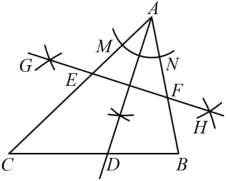 (1)、以点为圆心,以适当长为半径画弧,交于点 , 交于点.(2)分别以M,N为圆心,以大于的长为半径画弧,两弧在的内部相交于点.(3)作射线交于点D.(4)分别以A,D为圆心,以大于的长为半径画弧,两弧相交于G,H两点.(5)作直线 , 交分别于点E,F.
(1)、以点为圆心,以适当长为半径画弧,交于点 , 交于点.(2)分别以M,N为圆心,以大于的长为半径画弧,两弧在的内部相交于点.(3)作射线交于点D.(4)分别以A,D为圆心,以大于的长为半径画弧,两弧相交于G,H两点.(5)作直线 , 交分别于点E,F.依据以上作图,若 , , , 则的长是( ).
A、2 B、1 C、 D、43. 如图,长方形纸片中, 点是的中点,连接; 按以下步骤作图:①分别 以点和为圆心, 以大于的等长为半径作弧,两弧相交于点和;②作直线 , 且直线刚好经过点.若 , 则的长度是( ) A、2 B、 C、 D、44. 如图,在中, , 平分 , 交于点D,若点D恰好在边的垂直平分线上,则∠C的度数为( )
A、2 B、 C、 D、44. 如图,在中, , 平分 , 交于点D,若点D恰好在边的垂直平分线上,则∠C的度数为( ) A、30 B、36 C、40 D、455. 内找一点P,使P到B、C两点的距离相等,并且P到C的距离等于A到C的距离.下列尺规作图正确的是( )A、
A、30 B、36 C、40 D、455. 内找一点P,使P到B、C两点的距离相等,并且P到C的距离等于A到C的距离.下列尺规作图正确的是( )A、 B、
B、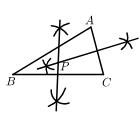 C、
C、 D、
D、 6. 如图,在△ABC中,按以下步骤作图:①分别以点A和点C为圆心,以大于的长为半径作弧,两弧相交于M、N两点;②作直线MN交BC于点D,连接AD.若AB=BD,AB=6,∠C=30°,则△ACD的面积为( )
6. 如图,在△ABC中,按以下步骤作图:①分别以点A和点C为圆心,以大于的长为半径作弧,两弧相交于M、N两点;②作直线MN交BC于点D,连接AD.若AB=BD,AB=6,∠C=30°,则△ACD的面积为( )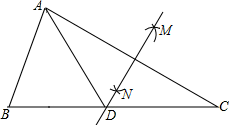 A、 B、 C、 D、97. 如图,在△ABC中,BC=3,AC=4,∠C=90°,以点B为圆心,BC长为半径画弧,与AB交于点D,再分别以A、D为圆心,大于AD的长为半径画弧,两弧交于点M、N,作直线MN,分别交AC、AB于点E、F,则AE的长度为( )
A、 B、 C、 D、97. 如图,在△ABC中,BC=3,AC=4,∠C=90°,以点B为圆心,BC长为半径画弧,与AB交于点D,再分别以A、D为圆心,大于AD的长为半径画弧,两弧交于点M、N,作直线MN,分别交AC、AB于点E、F,则AE的长度为( ) A、 B、3 C、 D、8. 如图,在矩形中,连接 , 分别以、为圆心,大于的长为半径画弧,两弧交于、两点,作直线 , 分别与、交于点、 , 连接、 . 若 , , 则四边形的周长为( )
A、 B、3 C、 D、8. 如图,在矩形中,连接 , 分别以、为圆心,大于的长为半径画弧,两弧交于、两点,作直线 , 分别与、交于点、 , 连接、 . 若 , , 则四边形的周长为( ) A、15 B、9 C、 D、9. 如图,在△ABC中,AB的垂直平分线分别交BC,AB于D,E两点,若 , △ADC的周长为9 cm,则△ABC的周长是( )
A、15 B、9 C、 D、9. 如图,在△ABC中,AB的垂直平分线分别交BC,AB于D,E两点,若 , △ADC的周长为9 cm,则△ABC的周长是( ) A、6 cm B、12 cm C、15 cm D、24 cm10. 如图,已知 , 用尺规在边上确定一点P,使 . 下面四种作图中,正确的是( )
A、6 cm B、12 cm C、15 cm D、24 cm10. 如图,已知 , 用尺规在边上确定一点P,使 . 下面四种作图中,正确的是( ) A、以B为圆心,为半径画弧,交于点P,点P为所求 B、以C为圆心,为半径画弧,交于点P,点P为所求 C、作的垂直平分线交于点P,点P为所求 D、作的垂直平分线交于点P,点P为所求
A、以B为圆心,为半径画弧,交于点P,点P为所求 B、以C为圆心,为半径画弧,交于点P,点P为所求 C、作的垂直平分线交于点P,点P为所求 D、作的垂直平分线交于点P,点P为所求二、填空题
-
11. 如图,在Rt△ABC中,∠B=90°,分别以A,C为圆心,大于AC长为半径画弧,两弧相交于点M,N,作直线MN,与AC,BC分别交于点D,点E,连结AE,当AC=13,AB=5时,则△ABE的周长是.
 12. 如图,在中,于点D,C是上一点, , 且点C在的垂直平分线上.若的周长为30,则的长为.
12. 如图,在中,于点D,C是上一点, , 且点C在的垂直平分线上.若的周长为30,则的长为. 13. 如图1,小明将一张长方形纸片对折,使长方形两边重合,折痕为EF,铺开后沿BC折叠,使点A与EF上的点D重合.如图2,再将该长方形纸片进行折叠,折痕分别为HG,KL,使长方形的两边均与EF重合;铺开后沿BP折叠,使点A与KL上的点Q重合;分别连结图1中的AD与图2中的AQ,则的值为.
13. 如图1,小明将一张长方形纸片对折,使长方形两边重合,折痕为EF,铺开后沿BC折叠,使点A与EF上的点D重合.如图2,再将该长方形纸片进行折叠,折痕分别为HG,KL,使长方形的两边均与EF重合;铺开后沿BP折叠,使点A与KL上的点Q重合;分别连结图1中的AD与图2中的AQ,则的值为.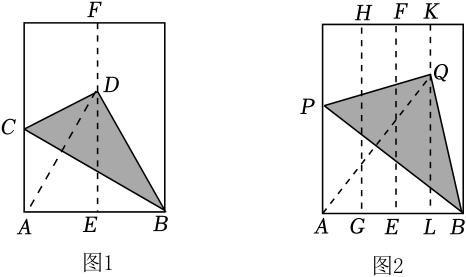 14. 如图,四边形ABCD是正方形,AB=6,E是BC的中点,连接DE,DE的垂直平分线分别交AB、DE、CD于点M、O、N,连接EN,过E作EF⊥EN交AB于点F,则AF的长为 .
14. 如图,四边形ABCD是正方形,AB=6,E是BC的中点,连接DE,DE的垂直平分线分别交AB、DE、CD于点M、O、N,连接EN,过E作EF⊥EN交AB于点F,则AF的长为 . 15. 如图,在中, , , , 以点B为圆心,长为半径画弧,与交于点D,再分别以A,D为圆心,大于的长为半径画弧,两弧交于点M,N,作直线 , 分别交 , 于点E,F,则线段的长为.
15. 如图,在中, , , , 以点B为圆心,长为半径画弧,与交于点D,再分别以A,D为圆心,大于的长为半径画弧,两弧交于点M,N,作直线 , 分别交 , 于点E,F,则线段的长为.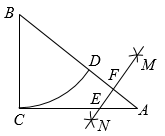
三、解答题
-
16. 如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC,垂足分别是E,F,连接EF,EF与BD相交于点P.求证:EP=FP.
 17. 如图,在中, , 是的垂直平分线,交于点E.已知的周长是24,的长是5.求的周长.
17. 如图,在中, , 是的垂直平分线,交于点E.已知的周长是24,的长是5.求的周长. 18. 如图,在中,点D是的中点,过点D作交于点E,连接 . 若的周长为13, , 求的周长.
18. 如图,在中,点D是的中点,过点D作交于点E,连接 . 若的周长为13, , 求的周长.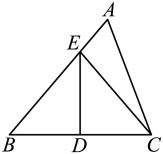
四、综合题
-
19. 如图,在中, , AB的垂直平分线DE分别交AC,AB于点D,E.
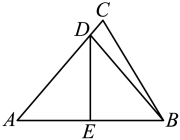 (1)、若 , 求的度数:(2)、若且周长为12,求BC的长.20. 如图,在四边形中, , 对角线的垂直平分线与边、分别相交于点M、N,连接、.
(1)、若 , 求的度数:(2)、若且周长为12,求BC的长.20. 如图,在四边形中, , 对角线的垂直平分线与边、分别相交于点M、N,连接、. (1)、求证:四边形是菱形;(2)、若四边形的周长为52, , 求的长.21. 如图,在中,分别以A,B为圆心,以大于的长为半径画弧,两弧交于M,N两点,直线交于点F,交BC于点E,D为线段的中点,.
(1)、求证:四边形是菱形;(2)、若四边形的周长为52, , 求的长.21. 如图,在中,分别以A,B为圆心,以大于的长为半径画弧,两弧交于M,N两点,直线交于点F,交BC于点E,D为线段的中点,. (1)、求证:;(2)、若 , 求的度数.22. 教材呈现
(1)、求证:;(2)、若 , 求的度数.22. 教材呈现以下是人教版八年级上册数学教材第53页的部分内容.
如图,四边形中, , .我们把这种两组邻边分别相等的四边形叫做“筝形”.

 (1)、【概念理解】根据上面教材的内容,请写出“筝形”的一条性质:;(2)、如图1,在中, , 垂足为 , 与关于所在的直线对称,与关于所在的直线对称,延长 , 相交于点.请写出图中的“筝形”: ;(写出一个即可)(3)、【应用拓展】如图2,在(2)的条件下,连接 , 分别交 , 于点 , , 连接.
(1)、【概念理解】根据上面教材的内容,请写出“筝形”的一条性质:;(2)、如图1,在中, , 垂足为 , 与关于所在的直线对称,与关于所在的直线对称,延长 , 相交于点.请写出图中的“筝形”: ;(写出一个即可)(3)、【应用拓展】如图2,在(2)的条件下,连接 , 分别交 , 于点 , , 连接.①求证:;
②求证:.
23. 如图,在中,已知 , 是边上的中线,点是边上一动点,点是上的一个动点.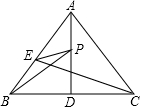 (1)、若 , 求的度数;(2)、若 , , , 且时,求的长;(3)、在(2)的条件下,请直接写出的最小值.
(1)、若 , 求的度数;(2)、若 , , , 且时,求的长;(3)、在(2)的条件下,请直接写出的最小值.