鲁教版（五四学制）2022-2023学年七年级数学下册10.1 全等三角形 同步测试

试卷更新日期：2023-03-11 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 如图，点B、E、C、F四点共线，∠B ＝∠DEF，BE ＝ CF，添加一个条件，不能判定 △ABC ≌ △DEF的是（   ）

    A、∠A＝∠D B、AB＝DE C、AC∥DF D、AC＝DF

    查看试题解析

  • 2. 如图，下列各组条件中，不能得到△ABC≌△BAD的是（       ）

    A、BC=AD ， ∠ABC=∠BAD B、BC=AD ， AC=BD C、AC=BD ， ∠CAB=∠DBA D、BC=AD ， ∠CAB=∠DBA

    查看试题解析

  • 3. 用直尺和圆规作一个角等于已知角，如图，要证∠A'O'B'=∠AOB ， 则只需证明△ODC≌△O'D'C' ， 依据是（  ）

    A、SAS B、SSS C、AAS D、ASA

    查看试题解析

  • 4. 如图，D是AB上一点，DF交AC于点E，DE=FE ， FC∥AB ， 若AB=7 ， CF=4 ， 则BD的长是（ ）

    A、5 B、4 C、3 D、2

    查看试题解析

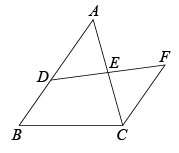  • 5. 如图，△ABC≅△CDA ， 则与BC长度相等的线段是（ ）

    A、CD B、CA C、DA D、AB

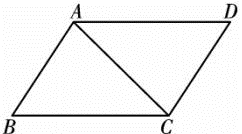    查看试题解析

  • 6. 如图，△OAB≌△OCD，若∠A＝80°，OB＝3，则下列说法正确的是（    ）

    A、∠COD＝80° B、CD＝3 C、∠D＝20° D、OD＝3

    查看试题解析

  • 7. 如图，AB=AD ， AC=AE ， ∠DAB=∠CAE=50° ， 以下四个结论：①△ADC≌△ABE；②CD=BE；③∠DOB=50°；④CD平分∠ACB ． 其中结论正确的个数是（ ）

    A、1 B、2 C、3 D、4

    查看试题解析

  • 8. 如图，在△ABC和△ADE中，已知AB=AD，还需要添加两个条件，才能使△ABC≌△ADE，不能添加的一组是（  ）

    A、BC=DE，AC=AE B、∠B=∠D，∠BAC=∠DAE C、BC=DE，∠C=∠E D、AC=AE，∠BAD=∠CAE

    查看试题解析

  • 9. 尺规作图作∠AOB的平分线方法如下：以O为圆心，任意长为半径画弧交OA、OB于C、D ， 再分别以点C、D为圆心，以大于12CD长为半径画弧，两弧交于点P ， 作射线OP ， 由作法得△OCP≌△ODP的根据是（  ）

    A、SAS B、ASA C、AAS D、SSS

    查看试题解析

  • 10. 如图，四边形ABCD ， ∠B=∠C=90° ， 边AD的中垂线分别交BC ， AD于点E ， F ， 且AF=EF若AB=5 ， CD=12 ， 则BE的长为（ ）

    A、7 B、12 C、13 D、17

    查看试题解析

二、填空题

  • 11. 如图，∠1=∠2=30° ， ∠A=∠B ， AE=BE ， 点D在边AC上，AE与BD相交于点O，则∠C的度数为 ．

    查看试题解析

  • 12. 如图，桌面上放置一个等腰直角△ABC，直角顶点C顶着桌面，若另外两个顶点与桌面的距离分别为5cm和3cm ， 过另外两个顶点向桌面作垂线，则两个垂足之间的距离DE的长度为cm ．

    查看试题解析

  • 13. 如图，有一座小山，现要在小山A，B的两端开一条隧道，施工队要知道A，B两端的距离，于是先在平地上取一个可以直接到达点A和点B的点C，连接AC并延长到D，使CD=CA ， 连接BC并延长到E，使CE=CB ， 连接DE ． 经测量DE ， EC ， DC的长度分别为800m ， 500m ， 400m ， 则A，B之间的距离为m；

    查看试题解析

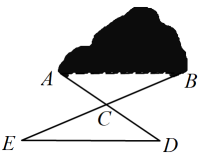  • 14. 如图，CD是△ABC的高，且CD平分∠ACB，∠BAC＝70°，∠CFE＝25°，则∠CEF＝°．

    查看试题解析

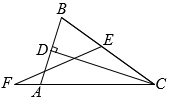  • 15. 如图，D是AB延长线上一点，DF交AC于点E，AE＝CE，FC∥AB，若AB＝3，CF＝5，则BD的长是 ．

    查看试题解析

三、解答题

  • 16. 已知：如图，点E，F是BD上的点，∠AED=∠CFB，AE=CF，BE=DF．

    求证：AB∥CD，AB=CD．

    查看试题解析

  • 17. 已知：点A、E、D、C在同一条直线上，AE=CD ， EF//BD ， EF=BD.求证：AB//CF.

    查看试题解析

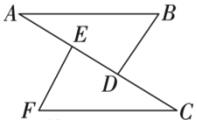  • 18. 在学习完“探索三角形全等的条件”一节后，小丽总结出很多全等三角形的模型，她设计了以下问题给同桌解决：如图，做一个“U”字形框架PABQ，AP，BQ足够长，PA⊥AB于点A，QB⊥AB于点B，她在框架里放了两根长度相等的木条CM、NM，且CM⊥MN，点C、M、N分别在PA、AB、BQ上，若AM＝4cm，求BN的长．

    查看试题解析

四、综合题

  • 19. 如图，在△ABC中，AD是BC边上的中线，F，E分别是AD及其延长线上的点．

    (1)、如果CF//BE，说明：△BDE≌△CDF；
    (2)、若CF，BE是△ABC的BC边上的中线AD及其延长线的垂线，垂足分别为E、F，请猜想BF与CE的位置关系？并说明理由．

    查看试题解析

  • 20. 如图，点E在线段CD上，EA、EB分别平分∠DAB和∠CBA，点F在线段AB上运动，AD=4cm，BC=3cm，且AD∥BC．

    (1)、你认为AE和BE有什么位置关系？并验证你的结论；
    (2)、当点F运动到离点A多少厘米时，△ADE和△AFE全等？为什么？
    (3)、在（2）的情况下，此时BF=BC吗？证明你的结论并求出AB的长.

    查看试题解析

  • 21. 已知如图，在△ABC中，D是BC的中点．过点D的直线GF交AC于点F，交AC的平行线BG于点G．

    (1)、试说明BG＝CF．
    (2)、若DE⊥GF交AB于点E，连接EF，试判断BE+CF与EF之间的大小关系，并说明理由．

    查看试题解析

  • 22. 如图在△ABC和△CDE中，AC=BC，CD=CE，∠ACB=∠DCE，连接AD，BE交于点M．

    (1)、如图1，当点B，C，D在同一条直线上，且∠ACB=∠DCE=45°时，可以得到图中的一对全等三角形，即≌；
    (2)、当点D不在直线BC上时，如图2位置，且∠ACB=∠DCE=α．

    ①试说明AD=BE；

    ②直接写出∠EMD的大小（用含α的代数式表示）．

    查看试题解析

  • 23. 在等腰Rt△ABC中，AB＝AC ， ∠BAC=90° ， 以CA为边在∠ACB的另一侧作∠ACM=∠ACB ， 点D为射线BC上任意一点，在射线CM上截取CE＝BD ， 连接AD、DE、AE ．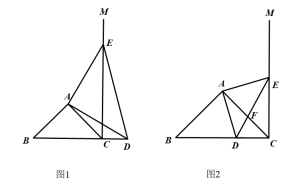

    (1)、如图1，当点D落在线段BC的延长线上时，试求∠ADE的度数；
    (2)、如图2，当点D落在线段BC（不与B、C重合）上时，AC与DE交于点F ， 请问（1）中的∠ADE的度数是否会改变?试说明理由．

    查看试题解析