冲刺2023中考——数学模拟考场仿真演练卷一
试卷更新日期:2023-03-11 类型:中考模拟
一、单选题(每题3分,共30分)
-
1. 计算 , 结果正确的是( )A、 B、 C、 D、2. 如图,M、N、P、Q是数轴上的点,那么在数轴上对应的点可能是( )
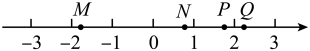 A、点A B、点N C、点P D、点Q3. 若关于x的不等式组仅有3个整数解,则a的取值范围是( )A、-4≤a<-2 B、-3<a≤-2 C、-3≤a≤-2 D、-3≤a<-24. 已知实数m,n满足 , 则的最大值为( )A、24 B、 C、 D、-45. 小明解方程的步骤如下:
A、点A B、点N C、点P D、点Q3. 若关于x的不等式组仅有3个整数解,则a的取值范围是( )A、-4≤a<-2 B、-3<a≤-2 C、-3≤a≤-2 D、-3≤a<-24. 已知实数m,n满足 , 则的最大值为( )A、24 B、 C、 D、-45. 小明解方程的步骤如下:解:方程两边同乘6,得①
去括号,得②
移项,得③
合并同类项,得④
以上解题步骤中,开始出错的一步是( )
A、① B、② C、③ D、④6. 如图,正比例函数与反比例函数的图象交于、B两点,当时,x的取值范围是( ) A、或 B、或 C、或 D、或7. 已知关于x的一元二次方程(m﹣1)x2+2x﹣3=0有实数根,则m的取值范围是( )A、m≥ B、m< C、m>且m≠1 D、m≥且m≠18. 如图,在菱形纸片ABCD中,E是BC边上一点,将△ABE沿直线AE翻折,使点B落在上,连接 . 已知∠C=120°,∠BAE=50°,则的度数为( )
A、或 B、或 C、或 D、或7. 已知关于x的一元二次方程(m﹣1)x2+2x﹣3=0有实数根,则m的取值范围是( )A、m≥ B、m< C、m>且m≠1 D、m≥且m≠18. 如图,在菱形纸片ABCD中,E是BC边上一点,将△ABE沿直线AE翻折,使点B落在上,连接 . 已知∠C=120°,∠BAE=50°,则的度数为( )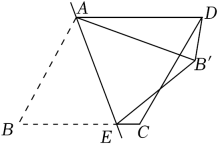 A、50° B、60° C、80° D、90°9. 如图,为的直径,弦交于点 , , , , 则( )
A、50° B、60° C、80° D、90°9. 如图,为的直径,弦交于点 , , , , 则( )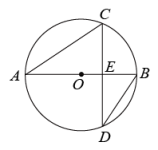 A、 B、 C、1 D、210. 如图是二次函数的图象,其对称轴为直线 , 且过点 . 有以下四个结论:① , ② , ③ , ④若顶点坐标为 , 当时,y有最大值为2、最小值为 , 此时m的取值范围是 . 其中正确结论的个数是( )
A、 B、 C、1 D、210. 如图是二次函数的图象,其对称轴为直线 , 且过点 . 有以下四个结论:① , ② , ③ , ④若顶点坐标为 , 当时,y有最大值为2、最小值为 , 此时m的取值范围是 . 其中正确结论的个数是( )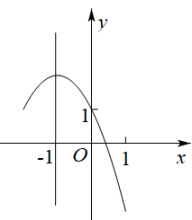 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题(每空3分,共18分)
-
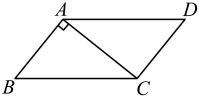
11. 如图,在中, , 若 , 则的度数是.
 12. 如图,以的三边为边在上方分别作等边、、.且点A在内部.给出以下结论:
12. 如图,以的三边为边在上方分别作等边、、.且点A在内部.给出以下结论:①四边形是平行四边形;
②当时,四边形是矩形;
③当时,四边形是菱形;
④当 , 且时,四边形是正方形.
其中正确结论有(填上所有正确结论的序号).
 13. 一艘轮船位于灯塔的南偏东方向,距离灯塔30海里的处,它沿北偏东方向航行一段时间后,到达位于灯塔的北偏东方向上的处,此时与灯塔的距离约为海里.(参考数据: , , )
13. 一艘轮船位于灯塔的南偏东方向,距离灯塔30海里的处,它沿北偏东方向航行一段时间后,到达位于灯塔的北偏东方向上的处,此时与灯塔的距离约为海里.(参考数据: , , )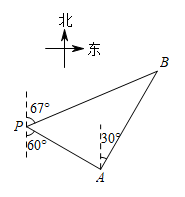 14. 如图,有一张平行四边形纸片 , , , 将这张纸片折叠,使得点落在边上,点的对应点为点 , 折痕为 , 若点在边上,则长的最小值等于 .
14. 如图,有一张平行四边形纸片 , , , 将这张纸片折叠,使得点落在边上,点的对应点为点 , 折痕为 , 若点在边上,则长的最小值等于 .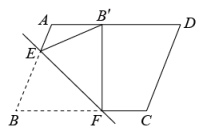 15. 喜迎党的二十大召开,学校推荐了四部影片:、香山叶正红、建党伟业、建军大业 . 甲、乙同学用抽卡片的方式决定本班观看哪部,四张卡片正面分别是上述影片剧照,除此之外完全相同.将这四张卡片背面朝上,甲随机抽出一张并放回,洗匀后,乙再随机抽出一张,则两人恰好抽到同一部的概率是 .16. 小明在学习“二次函数”内容后,进行了反思总结.如图,二次函数y=ax2+bx+c(a≠0)图像的一部分与x轴的一个交点坐标为(1,0),对称轴为直线x=﹣1,结合图像他得出下列结论:①ab>0且c>0;②a+b+c=0;③关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为﹣3和1;④若点(﹣4,y1),(﹣2,y2),(3,y3)均在二次函数图象上,则y1<y2<y3;⑤3a+c<0,其中正确的结论有 . (填序号,多选、少选、错选都不得分)
15. 喜迎党的二十大召开,学校推荐了四部影片:、香山叶正红、建党伟业、建军大业 . 甲、乙同学用抽卡片的方式决定本班观看哪部,四张卡片正面分别是上述影片剧照,除此之外完全相同.将这四张卡片背面朝上,甲随机抽出一张并放回,洗匀后,乙再随机抽出一张,则两人恰好抽到同一部的概率是 .16. 小明在学习“二次函数”内容后,进行了反思总结.如图,二次函数y=ax2+bx+c(a≠0)图像的一部分与x轴的一个交点坐标为(1,0),对称轴为直线x=﹣1,结合图像他得出下列结论:①ab>0且c>0;②a+b+c=0;③关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为﹣3和1;④若点(﹣4,y1),(﹣2,y2),(3,y3)均在二次函数图象上,则y1<y2<y3;⑤3a+c<0,其中正确的结论有 . (填序号,多选、少选、错选都不得分)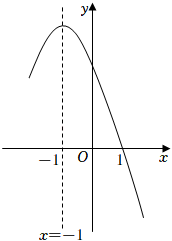
三、解答题(共9题,共72分)
-
17. 解不等式组: , 并写出它的正整数解.18. 计算: .19. 教育部在《大中小学劳动教育指导纲要(试行)》中明确要求:初中生每周课外生活和家庭生活中,劳动时间不少于3小时.某走读制初级中学为了解学生劳动时间的情况,对学生进行了随机抽样调查,并将调查结果制成不完整的统计图表,如图:
平均每周劳动时间的频数统计表
劳动时间小时
频数
t<3
9
3≤t<4
a
4≤t<5
66
t≥5
15

请根据图表信息,回答下列问题.
(1)、参加此次调查的总人数是人,频数统计表中a=;(2)、在扇形统计图中,D组所在扇形的圆心角度数是°;(3)、该校准备开展以“劳动美”为主题的教育活动,要从报名的2男2女中随机挑选2人在活动中分享劳动心得,请用树状图或列表法求恰好抽到一名男生和一名女生的概率.20. “五一”节期间,许多露营爱好者在我市郊区露营,为遮阳和防雨会搭建一种“天幕”,其截面示意图是轴对称图形,对称轴是垂直于地面的支杆 , 用绳子拉直后系在树干上的点处,使得 , , 在一条直线上,通过调节点的高度可控制“天幕”的开合,m,m.
(参考数据: , , , )
(1)、天晴时打开“天幕”,若 , 求遮阳宽度(结果精确到0.1m);(2)、下雨时收拢“天幕”,从65°减少到45°,求点下降的高度(结果精确到0.1m).21. 如图,是的内接三角形, , 经过圆心交于点 , 连接 , . (1)、判断直线与的位置关系,并说明理由;(2)、若 , 求图中阴影部分的面积.22. 阅读材料,解答问题:
(1)、判断直线与的位置关系,并说明理由;(2)、若 , 求图中阴影部分的面积.22. 阅读材料,解答问题:材料1
为了解方程 , 如果我们把看作一个整体,然后设 , 则原方程可化为 , 经过运算,原方程的解为 , . 我们把以上这种解决问题的方法通常叫做换元法.
材料2
已知实数m,n满足 , , 且 , 显然m,n是方程的两个不相等的实数根,由书达定理可知 , .
根据上述材料,解决以下问题:
(1)、直接应用:方程的解为;
(2)、间接应用:已知实数a,b满足: , 且 , 求的值;
(3)、拓展应用:已知实数m,n满足: , 且 , 求的值.
23. 如图,在平面直角坐标系中,直线与轴、轴分别交于点、两点,与双曲线交于点、两点, .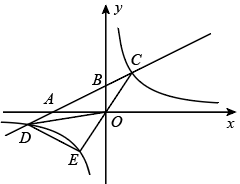 (1)、求 , 的值;(2)、求点坐标并直接写出不等式的解集;(3)、连接并延长交双曲线于点 , 连接、 , 求的面积.24. 如图,在菱形ABCD中,AB=5,BD为对角线.点E是边AB延长线上的任意一点,连结DE交BC于点F,BG平分∠CBE交DE于点G.
(1)、求 , 的值;(2)、求点坐标并直接写出不等式的解集;(3)、连接并延长交双曲线于点 , 连接、 , 求的面积.24. 如图,在菱形ABCD中,AB=5,BD为对角线.点E是边AB延长线上的任意一点,连结DE交BC于点F,BG平分∠CBE交DE于点G. (1)、求证:.(2)、若 .
(1)、求证:.(2)、若 .①求菱形的面积.
②求的值.
(3)、若 , 当的大小发生变化时(),在AE上找一点T,使GT为定值,说明理由并求出ET的值.25. 如图(1),二次函数的图象与轴交于、两点,与轴交于点,点的坐标为 , 点的坐标为 , 直线经过、两点.
 (1)、求该二次函数的表达式及其图象的顶点坐标;(2)、点为直线上的一点,过点作轴的垂线与该二次函数的图象相交于点 , 再过点作轴的垂线与该二次函数的图象相交于另一点 , 当时,求点的横坐标;(3)、如图(2),点关于轴的对称点为点 , 点为线段上的一个动点,连接 , 点为线段上一点,且 , 连接 , 当的值最小时,直接写出的长.
(1)、求该二次函数的表达式及其图象的顶点坐标;(2)、点为直线上的一点,过点作轴的垂线与该二次函数的图象相交于点 , 再过点作轴的垂线与该二次函数的图象相交于另一点 , 当时,求点的横坐标;(3)、如图(2),点关于轴的对称点为点 , 点为线段上的一个动点,连接 , 点为线段上一点,且 , 连接 , 当的值最小时,直接写出的长.