河北省石家庄市赵县2022-2023学年第一学期八年级数学期末试卷

试卷更新日期：2023-03-10 类型：期末考试

进入出卷网下载

一、选择题．(本大题有16个小题，1~10小题每题3分；11~16小题每题2分，共42分.)

1. 已知三条线段的长分别是4，4，m，若它们能构成三角形，则整数m的最大值是（）

A、10 B、8 C、7 D、4

查看试题解析
2. 如图是一个平分角的仪器，其中AB=AD，BC=DC，将点A放在角的顶点，AB和AD沿着角的两边放下，沿AC画一条射线，这条射线就是角的平分线，在这个操作过程中，运用了三角形全等的判定方法是（）

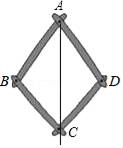A、SSS B、SAS C、ASA D、AAS

查看试题解析
3. 如图，在 $△ A B C$ 和 $△ D E F$ 中，点 $A$ ， $E$ ， $B$ ， $D$ 在同一直线上， $A C ∥ D F$ ， $A C = D F$ ，只添加一个条件，能判定 $△ A B C ≌ △ D E F$ 的是（）

A、 $B C = D E$ B、 $A E = D B$ C、 $∠ A = ∠ D E F$ D、 $∠ A B C = ∠ D$

查看试题解析
4. 到△ABC的三条边距离相等的点是△ABC的（）

A、三条中线交点 B、三条角平分线交点 C、三条高的交点 D、三条边的垂直平分线交点

查看试题解析
5. 下列计算正确的是（）

A、m+m=m² B、(-3x)²=6x² C、(m+2n)²=m²+4n² D、(m+3)(m-3)=m²-9

查看试题解析
6. 如图，△ABC中，D点在AB上，E点在BC上，DE为AB的中垂线．若∠B=∠C，且∠EAC>90°，则根据图中标示的角，下列结论正确的是（）

A、∠1=∠2，∠1<∠3 B、∠1=∠2，∠1>∠3 C、∠l≠∠2，∠1<∠3 D、∠1≠∠2，∠1>∠3

查看试题解析
7. 下列变形从左到右是因式分解的是（）

A、(x+1)(x-1)=x²-1 B、x²+2x+1=x(x+2)+1 C、-2x(x+y)=-2x²-2xy D、x²-12x+36=(x-6)²

查看试题解析
8. 如果(x+1)(2x+m)的乘积中不含x的一次项，则m的值为（）

A、2 B、-2 C、0.5 D、-0.5

查看试题解析
9. 若 $a \neq b$ ，则下列分式化简正确的是（）

A、 $\frac{a + 2}{b + 2} = \frac{a}{b}$ B、 $\frac{a - 2}{b - 2} = \frac{a}{b}$ C、 $\frac{a^{2}}{b^{2}} = \frac{a}{b}$ D、 $\frac{\frac{1}{2} a}{\frac{1}{2} b} = \frac{a}{b}$

查看试题解析
10. 某药店在今年3月份购进了一批口罩，这批口罩包括一次性医用外科口罩和N95口罩，且两种口罩的只数相同，其中一次性医用外科口罩花费1600元，N95口罩花费9600元．已知一次性医用外科口罩的单价比N95口罩的单价少10元，那么一次性医用外科口罩的单价为多少元？设一次性医用外科口罩单价为x元，则列方程正确的是（）

A、 $\frac{9000}{x - 10} = \frac{1600}{x}$ B、 $\frac{9600}{x + 10} = \frac{1600}{x}$ C、 $\frac{9600}{x} = \frac{1600}{x - 10}$ D、 $\frac{9600}{x} = \frac{1600}{x} + 10$

查看试题解析
11. 若x是非负整数，则表示 $\frac{2 x}{x + 2} - \frac{x^{2} - 4}{(x + 2)^{2}}$ 的值的对应点落在如图数轴上的范围是（）

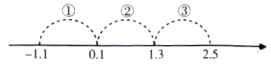A、① B、② C、③ D、①或②

查看试题解析
12. 在等腰△ABC中，AB=AC，中线BD将这个三角形的周长分为15和12两个部分，则这个等腰三角形的底边长为（）

A、7 B、11 C、7或11 D、7或10

查看试题解析
13. 3⁵⁰ ， 4⁴⁰ ， 5³⁰的大小关系是（）

A、3⁵⁰<4⁴⁰<5³⁰ B、5³⁰<3⁵⁰<4⁴⁰ C、5³⁰<4⁴⁰<3⁵⁰ D、4⁴⁰<5³⁰<3⁵⁰

查看试题解析
14. 如果关于x的方程 $\frac{2 x + m}{x - 1}$ =1的解是正数，那么m的取值范围是（）

A、m>-1 B、m>-1且m≠0 C、m<-1 D、m<-1且m≠-2

查看试题解析
15. 如图，△ABC是等边三角形，AD是BC边上的高，E是AC的中点，P是AD上的一个动点，当PC与PE的和最小时，∠CPE的度数是（）

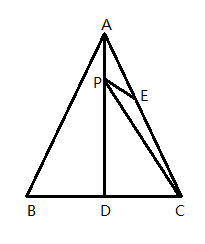A、30° B、45° C、60° D、90°

查看试题解析
16. 在平面直角坐标系×Oy中，点A(0，2)，B(a，0)，C(m，n)(n>0)．若△ABC是等腰直角三角形，且AB= BC，当0<a<1时，点C的横坐标m的取值范围是：（）

A、0<m<2 B、2<m<3 C、m<3 D、m>3

查看试题解析

二、填空题(本大题共3个小题，每小题3分，共9分．其中18小题第一空2分，第二空1分；19小题每空1分)

17. 有一种新冠病毒直径为0.00000012米，数0.00000012用科学记数法表示为

查看试题解析
18. 现有甲、乙、丙三种不同的矩形纸片（边长如图）．

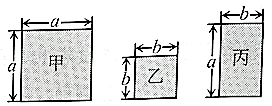(1)、取甲、乙纸片各1块，其面积和为；

(2)、嘉嘉要用这三种纸片紧密拼接成一个大正方形，先取甲纸片1块，再取乙纸片4块，还需取丙纸片块．

查看试题解析
19. 在△ABC中，D是BC边的点(不与点B、C重合)，连接AD．

(1)、如图1，当点D是BC边上的中点时，S_△_ABD：S_△_ACD=

(2)、如图2，当AD是∠BAC的平分线时，若AB=m，AC=n，则S_△_ABD：S_△_ACD =(用含m，n的代数式表示)

(3)、如图3，AD平分∠BAC，延长AD到E，使得AD=DE，连接BE，如果AC=2，AB=4，S_△_BDE=6，那么S_△_ABC= ．

查看试题解析

三、解答题．(本大题共7个小题，共69分．)

20.

(1)、解方程： $\frac{x}{x - 1} - 1 = \frac{3}{(x - 1) (x + 2)}$

(2)、先化简，再求值：[(x+y)(x-2y)-(x-2y)²]÷ $\frac{1}{2}$ y，其中x=-1，y= $- \frac{1}{4}$

查看试题解析
21. 以下是某同学化简分式 $(\frac{x + 1}{x^{2} - 4} - \frac{1}{x + 2}) \div \frac{3}{x - 2}$ 的部分运算过程：
解：原式= $[\frac{x + 1}{(x + 2) (x - 2)} - \frac{1}{x + 2}] \times \frac{x - 2}{3}$ ①

= $[\frac{x + 1}{(x + 2) (x - 2)} - \frac{x - 2}{(x + 2) (x - 2)}] \times \frac{x - 2}{3}$ ②

= $\frac{x + 1 - x - 2}{(x + 2) (x - 2)} \times \frac{x - 2}{3}$ ③

．．．

(1)、上面的运算过程中第步出现了错误；

(2)、请你写出完整的解答过程．

查看试题解析
22. 如图，点A，B，C，D在一条直线上，且 $A B = C D$ ，若 $∠ 1 = ∠ 2$ ， $E C = F B .$ 求证： $∠ E = ∠ F$ .

查看试题解析
23. 如图，在Rt△ABC中，
(要求：尺规作图，不写作法，保留作图痕迹，并把作图痕迹用黑色签字笔描黑)
⑴利用尺规作图，在BC边上求作一点P，使得点P到AB的距离(PD的长)等于PC的长；
⑵利用尺规作图，作出(1)中的线段PD．

查看试题解析
24. 设a5是一个两位数，其中a是十位上的数字(1≤a≤9)．例如，当a=4时，a5表示的两位数是45．

(1)、尝试：
①当a=1时，15²=225=1×2×100+25 ；
②当a=2时，25²=625=2×3×100+25；
③当a=3时，35²= 1225=；
．．．．．．

(2)、归纳： $\overset{— — 2}{a 5}$ 与100a(a+1)+ 25有怎样的大小关系？试说明理由．

(3)、运用：若 $\overset{— — 2}{a 5}$ 与100a的差为2525，求a的值．

查看试题解析
25. 已知：在△ABC中，AB=AC，D为AC的中点，DE⊥AB，DF⊥BC，垂足分别为点E，F，且DE=DF。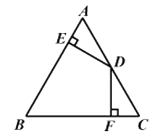
求证：△ABC是等边三角形。

查看试题解析
26. △ABC和△ADE都是等边三角形．

(1)、将△ADE绕点A旋转到图①的位置时，连接BD，CE并延长相交于点P(点P与点A重合)，有PA+PB=PC(或PA+ PC= PB)成立(不需证明)；
将△ADE绕点A旋转到图②的位置时，连接BD，CE相交于点P ，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？并加以证明；

(2)、将△ADE绕点A旋转到图③的位置时，连接BD，CE相交于点P，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？并加以证明．

查看试题解析