山东省菏泽市2023届高三下学期数学一模联考试卷
试卷更新日期:2023-03-10 类型:高考模拟
一、单选题
-
1. 已知集合 , 则( )A、 B、 C、或 D、或2. 设i是虚数单位,复数 , 则( )A、 B、 C、 D、3. 2020年12月17日凌晨1时59分,嫦娥五号返回器携带月球样品成功着陆,这是我国首次实现了地外天体采样返回,标志着中国航天向前又迈出了一大步.月球距离地球约38万千米,有人说:在理想状态下,若将一张厚度约为0.1毫米的纸对折次其厚度就可以超过到达月球的距离,那么至少对折的次数是( )( , )A、40 B、41 C、42 D、434. 如图,八面体的每一个面都是正三角形,并且四个顶点在同一平面内,下列结论:①平面;②平面平面;③;④平面平面 , 正确命题的个数为( )
 A、1 B、2 C、3 D、45. 过抛物线焦点作倾斜角为的直线交抛物线于 , 则( )A、 B、 C、1 D、166. 为了迎接“第32届菏泽国际牡丹文化旅游节”,某宣传团体的六名工作人员需要制作宣传海报,每人承担一项工作,现需要一名总负责,两名美工,三名文案,但甲,乙不参与美工,丙不能书写文案,则不同的分工方法种数为( )A、9种 B、11种 C、15种 D、30种7. 设实数满足 , , , 则的最小值为( )A、 B、 C、 D、8. 定义在实数集上的函数 , 如果 , 使得 , 则称为函数的不动点.给定函数 , , 已知函数 , , 在上均存在唯一不动点,分别记为 , 则( )A、 B、 C、 D、
A、1 B、2 C、3 D、45. 过抛物线焦点作倾斜角为的直线交抛物线于 , 则( )A、 B、 C、1 D、166. 为了迎接“第32届菏泽国际牡丹文化旅游节”,某宣传团体的六名工作人员需要制作宣传海报,每人承担一项工作,现需要一名总负责,两名美工,三名文案,但甲,乙不参与美工,丙不能书写文案,则不同的分工方法种数为( )A、9种 B、11种 C、15种 D、30种7. 设实数满足 , , , 则的最小值为( )A、 B、 C、 D、8. 定义在实数集上的函数 , 如果 , 使得 , 则称为函数的不动点.给定函数 , , 已知函数 , , 在上均存在唯一不动点,分别记为 , 则( )A、 B、 C、 D、二、多选题
-
9. 为了解学生的身体状况,某校随机抽取了100名学生测量体重,经统计,这些学生的体重数据(单位:千克)全部介于45至70之间,将数据整理得到如图所示的频率分布直方图,则( )
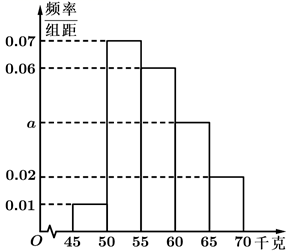 A、频率分布直方图中 的值为0.04 B、这100名学生中体重不低于60千克的人数为20 C、这100名学生体重的众数约为52.5 D、据此可以估计该校学生体重的75%分位数约为61.2510. 已知圆 , 下列说法正确有( )A、对于 , 直线与圆都有两个公共点 B、圆与动圆有四条公切线的充要条件是 C、过直线上任意一点作圆的两条切线(为切点),则四边形的面积的最小值为4 D、圆上存在三点到直线距离均为111. 已知函数 , 下列命题正确的有( )A、在区间上有3个零点 B、要得到的图象,可将函数图象上的所有点向右平移个单位长度 C、的周期为 , 最大值为1 D、的值域为12. 已知双曲线的左、右焦点分别为、 , 过点的直线与双曲线的左、右两支分别交于、两点,下列命题正确的有( )A、当点为线段的中点时,直线的斜率为 B、若 , 则 C、 D、若直线的斜率为 , 且 , 则
A、频率分布直方图中 的值为0.04 B、这100名学生中体重不低于60千克的人数为20 C、这100名学生体重的众数约为52.5 D、据此可以估计该校学生体重的75%分位数约为61.2510. 已知圆 , 下列说法正确有( )A、对于 , 直线与圆都有两个公共点 B、圆与动圆有四条公切线的充要条件是 C、过直线上任意一点作圆的两条切线(为切点),则四边形的面积的最小值为4 D、圆上存在三点到直线距离均为111. 已知函数 , 下列命题正确的有( )A、在区间上有3个零点 B、要得到的图象,可将函数图象上的所有点向右平移个单位长度 C、的周期为 , 最大值为1 D、的值域为12. 已知双曲线的左、右焦点分别为、 , 过点的直线与双曲线的左、右两支分别交于、两点,下列命题正确的有( )A、当点为线段的中点时,直线的斜率为 B、若 , 则 C、 D、若直线的斜率为 , 且 , 则三、填空题
-
13. 已知夹角为的非零向量满足 , , 则.14. 定义在上的函数 , 满足为偶函数,为奇函数,若 , 则.15. 设均为非零实数,且满足 , 则.16. 正三棱锥的高为为中点,过作与棱平行的平面,将三棱锥分为上下两部分,设上、下两部分的体积分别为 , 则.
四、解答题
-
17. 如图,在平面四边形中, , .
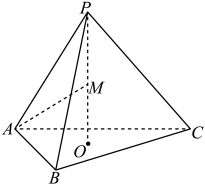
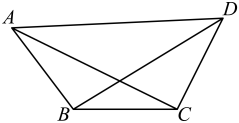 (1)、试用表示的长;(2)、求的最大值.18. 为了促进学生德、智、体、美、劳全面发展,某校成立了生物科技小组,在同一块试验田内交替种植A、B、C三种农作物(该试验田每次只能种植一种农作物),为了保持土壤肥度,每种农作物都不连续种植,共种植三次.在每次种植后会有的可能性种植的可能性种植;在每次种植的前提下再种植的概率为 , 种植的概率为 , 在每次种植的前提下再种植的概率为 , 种植的概率为.(1)、在第一次种植的前提下,求第三次种植的概率;(2)、在第一次种植的前提下,求种植作物次数的分布列及期望.19. 如图,直四棱柱中, , 与交于为棱上一点,且 , 点到平面的距离为.
(1)、试用表示的长;(2)、求的最大值.18. 为了促进学生德、智、体、美、劳全面发展,某校成立了生物科技小组,在同一块试验田内交替种植A、B、C三种农作物(该试验田每次只能种植一种农作物),为了保持土壤肥度,每种农作物都不连续种植,共种植三次.在每次种植后会有的可能性种植的可能性种植;在每次种植的前提下再种植的概率为 , 种植的概率为 , 在每次种植的前提下再种植的概率为 , 种植的概率为.(1)、在第一次种植的前提下,求第三次种植的概率;(2)、在第一次种植的前提下,求种植作物次数的分布列及期望.19. 如图,直四棱柱中, , 与交于为棱上一点,且 , 点到平面的距离为.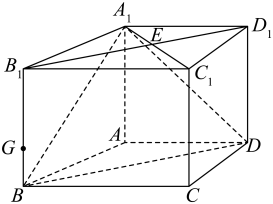 (1)、判断是否在平面内,并说明理由;(2)、求平面与平面所成角的余弦值.
(1)、判断是否在平面内,并说明理由;(2)、求平面与平面所成角的余弦值.