浙江省十校联盟2023届高三下学期数学2月第三次联考试卷
试卷更新日期:2023-03-10 类型:高考模拟
一、单选题
-
1. 已知集 , , 则( )A、 B、 C、 D、2. 已知复数 , , 则复数的模等于( )A、 B、 C、 D、3. 函数的图像是( )A、
 B、
B、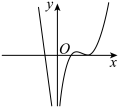 C、
C、 D、
D、 4. 已知向量满足 , , , 则( )A、 B、 C、 D、5. 记为数列的前n项积,已知 , 则( )A、8 B、9 C、10 D、116. 已知函数在上单调递增,且 , 则( )A、 B、 C、 D、7. 甲、乙、丙3人去食堂用餐,每个人从这5种菜中任意选用2种,则菜有2人选用、菜有1人选用的情形共有( )A、54 B、81 C、135 D、1628. 若函数满足 , , 设的导函数为 , 当时, , 则( )A、65 B、70 C、75 D、80
4. 已知向量满足 , , , 则( )A、 B、 C、 D、5. 记为数列的前n项积,已知 , 则( )A、8 B、9 C、10 D、116. 已知函数在上单调递增,且 , 则( )A、 B、 C、 D、7. 甲、乙、丙3人去食堂用餐,每个人从这5种菜中任意选用2种,则菜有2人选用、菜有1人选用的情形共有( )A、54 B、81 C、135 D、1628. 若函数满足 , , 设的导函数为 , 当时, , 则( )A、65 B、70 C、75 D、80二、多选题
-
9. 已知定义域为I的偶函数在上单调递增,且 , 使.则下列函数中符合上述条件的是( )A、 B、 C、 D、10. 已知随机变量从二项分布 , 则( )A、 B、 C、 D、最大时或50111. 已知椭圆的左、右焦点分别为 , 点在椭圆上且在轴上方,若的中点在以原点为圆心,为半径的圆上,则( )A、点在第一象限 B、的面积为 C、的斜率为 D、直线和圆相切12. 数列定义如下: , , 若对于任意 , 数列的前项已定义,则对于 , 定义 , 为其前n项和,则下列结论正确的是( )A、数列的第项为 B、数列的第2023项为 C、数列的前项和为 D、
三、填空题
-
13. 展开式中项的系数为.14. 已知随机事件A,B, , , , 则.15. 在中,E为边BC中点,若 , 的外接圆半径为3,则的最大值为.16. 在三棱锥中,对棱 , , , 则该三棱锥的外接球体积为 , 内切球表面积为.
四、解答题
-
17. 某地区2016至2022年生活垃圾无害化处理量(单位:万吨)如下表:
年份
2016
2017
2018
2019
2020
2021
2022
年份代号x
1
2
3
4
5
6
7
生活垃圾无害化处理量y
3.9
4.3
4.6
5.4
5.8
6.2
6.9
附:回归直线的斜率和截距的最小二乘估计公式分别为: , .参考数据
(1)、求y关于x的线性回归方程;(2)、根据(1)中的回归方程,分析过去七年该地区生活垃圾无害化处理的变化情况,并预测该地区2024年生活垃圾无害化处理量.18. 如图,在中,D为边BC上一点, , , , . (1)、求的大小;(2)、求的面积.19. 在数列中 , , 在数列中 , .(1)、求证数列成等差数列并求;(2)、求证:.
(1)、求的大小;(2)、求的面积.19. 在数列中 , , 在数列中 , .(1)、求证数列成等差数列并求;(2)、求证:.
