云南省红河州2023届高三数学第一次复习统一检测（一模）试卷

试卷更新日期：2023-03-10 类型：高考模拟

进入出卷网下载

一、单选题

1. 若集合 $M = {x | x^{\frac{1}{2}} < 9}$ ， $N = {x | x^{2} \geq 1}$ ，则 $M ∩ N =$ （）

A、 ${x | x \leq - 1$ 或 $1 \leq x < 3}$ B、 ${x | 1 \leq x < 3}$ C、 ${x | 1 \leq x < 81}$ D、 ${x | x \leq - 1$ 或 $1 \leq x < 81}$

查看试题解析
2. 复数 $\frac{1}{\frac{1}{2} + \frac{\sqrt{3}}{2} i}$ 与下列哪个复数相等（）

A、 $c o s (- \frac{π}{3}) + i s i n (- \frac{π}{3})$ B、 $\frac{\sqrt{3}}{2} - \frac{1}{2} i$ C、 $1 - i$ D、 $\frac{π}{3} i$

查看试题解析
3. 已知向量 $\vec{a} = (2 ， m)$ ， $\vec{b} = (4 ， - 1)$ ，且 $(\vec{a} - \vec{b}) ⊥ (\vec{a} + \vec{b})$ ，则实数 $m =$ （）

A、2 B、 $\frac{1}{2}$ C、8 D、 $\pm \sqrt{13}$

查看试题解析
4. 中国是茶的故乡，也是茶文化的发源地，茶文化是把茶、赏茶、闻茶、饮茶、品茶等习惯与中国的文化内涵相结合而形成的一种文化现象，具有鲜明的中国文化特征．其中沏茶、饮茶对水温也有一定的要求，把物体放在空气中冷却，如果物体原来的温度是 ${θ_{1}}^{∘} C$ ，空气的温度是 ${θ_{0}}^{∘} C$ ，经过t分钟后物体的温度为θ℃，满足公式 $θ = θ_{0} + (θ_{1} - θ_{0}) e^{- 0.25 t}$ ．现有一壶水温为92℃的热水用来沏茶，由经验可知茶温为52℃时口感最佳，若空气的温度为12℃，那从沏茶开始，大约需要（）分钟饮用口感最佳．（参考数据； $l n 3 \approx 1.099$ ， $l n 2 \approx 0.693$ ）

A、2.57 B、2.77 C、2.89 D、3.26

查看试题解析
5. 如图所示是一块边长为10cm的正方形铝片，其中阴影部分由四个全等的等腰梯形和一个正方形组成，将阴影部分裁剪下来，并将其拼接成一个无上盖的容器（铝片厚度不计），则该容器的容积为（）

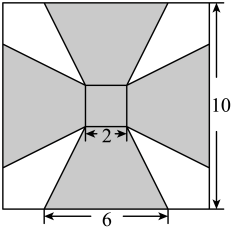A、 $\frac{80 \sqrt{3}}{3} c m^{3}$ B、 $\frac{104 \sqrt{3}}{3} c m^{3}$ C、 $80 \sqrt{3} c m^{3}$ D、 $104 \sqrt{3} c m^{3}$

查看试题解析
6. 一组数据为148，150，151，153，153，154，155，156，156，158，163，165，则这组数据的上四分位数是（）

A、151 B、152 C、156 D、157

查看试题解析
7. 古希腊数学家阿波罗尼奥斯的著作《圆锥曲线论》中有这样一个命题：平面内与两定点的距离的比为常数k（ $k > 0$ 且 $k \neq 1$ ）的点的轨迹为圆，后人将这个圆称为阿波罗尼奥斯圆．已知点 $O (0 ， 0) ， A (5 ， 0) ，$ 圆C： ${(x - 4)}^{2} + y^{2} = r^{2} (r > 0)$ 上有且只有一个点P满足 $\frac{| P A |}{| P O |} = \frac{3}{2}$ ，则r的值是（）

A、2 B、8 C、8或14 D、2或14

查看试题解析
8. 已知函数 $f (x) = s i n (ω x + φ) (ω > 0 ， | φ | < \frac{π}{2})$ ．若 $f (x + \frac{π}{6})$ 为偶函数． $y = f (x)$ 的图象与x轴交点的横坐标构成一个公差为 $\frac{π}{2}$ 的等差数列．将函数 $f (x)$ 图象上每一点的横坐标缩短为原来的 $\frac{1}{2}$ ，纵坐标不变，再向左平移 $\frac{π}{12}$ 个单位后得到函数 $g (x)$ 的图象，则 $f (\frac{π}{3}) + g (\frac{π}{3})$ （）

A、0 B、－2 C、1 D、－1

查看试题解析

二、多选题

9. 某校高三一名数学教师从该校高三学生中随机抽取男、女生各50名进行了身高统计，得到男、女身高分别近似服从正态分布

N (173 ， 11)

和

N (164 ， 9)

，并对其是否喜欢体育锻炼进行数据统计，得到如下2×2列联表：

	喜欢	不喜欢	合计
男生	37	m	50
女生	n	32	50
合计	55	45	100

参考公式： $χ^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d}$

α	0.01	0.005	0.001
$x_{α}$	6.635	7.879	10.828

则下列说法正确的是（）

A、

m = 13

，

n = 18

B、男生身高的平均数约为173，女生身高的平均数约为164 C、男生身高的标准差约为11，女生身高的标准差约为9 D、依据

α = 0.01

的独立性检验，认为喜欢体育锻炼与性别有关联

查看试题解析

10. 已知 $x > 0$ ， $y > 0$ ，且 $x + y - x y + 3 = 0$ ，则下列说法正确的是（）

A、 $3 < x y ≤ 12$ B、 $x + y \geq 6$ C、 $x^{2} + y^{2} ≥ 18$ D、 $0 < \frac{1}{x} + \frac{1}{y} ≤ \frac{1}{3}$

查看试题解析
11. 三棱锥P－ABC的四个顶点都在球O上，且PA⊥底面ABC， $P A = 2 A B = 2 A C = 2$ ， $∠ B A C = \frac{2 π}{3}$ ，则下列说法正确的是（）

A、 $B C = \sqrt{3}$ B、球心O在三棱锥的外部 C、球心O到底面ABC的距离为2 D、球O的体积为 $\frac{8 \sqrt{2} π}{3}$

查看试题解析
12. 已知函数 $f (x) = {\begin{array}{l} \frac{1}{e^{| l n x |}} ， x \in (0 ， + ∞) \\ l n (1 - x) ， x \in (- ∞ ， 0] \end{array}$ ，则下列说法正确的是（）

A、函数 $f (x)$ 有两个极值点 B、若关于x的方程 $f (x) = t$ 恰有1个解，则 $t > 1$ C、函数 $f (x)$ 的图象与直线 $x + y + c = 0 (c \in R)$ 有且仅有一个交点 D、若 $f (x_{1}) = f (x_{2}) = f (x_{3})$ ，且 $x_{1} < x_{2} < x_{3}$ ，则 $(1 - x_{1}) (x_{2} + x_{3})$ 无最值

查看试题解析

三、填空题

13. $(1 + \frac{y}{x}) {(x - y)}^{7}$ 的展开式中 $x^{2} y^{5}$ 的系数为．（用数字作答）

查看试题解析
14. 在数列 ${a_{n}}$ 中， $a_{3} = 3$ ， $a_{5} = 7$ ，若 ${2 a_{n} - n}$ 为等比数列，则 $a_{11} =$ ．

查看试题解析
15. 已知函数 $f (x) = x^{3} + 2 x - 1 + {(s i n x - c o s x)}^{2}$ ，则不等式 $f (x^{2} - 2 x) + f (2 - x) > 0$ 的解集为．

查看试题解析
16. 已知双曲线E： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点分别为 $F_{1}$ 、 $F_{2}$ ，若E上存在点P，满足 $| O P | = \frac{1}{2} | F_{1} F_{2} |$ ，（O为坐标原点），且 $△ P F_{1} F_{2}$ 的内切圆的半径等于a，则E的离心率为．

查看试题解析

四、解答题

17. 已知正项数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，且满足 $2 a_{n} + 1 = 2 \sqrt{2 S_{n}}$ ．

(1)、求数列 ${a_{n}}$ 的通项公式：

(2)、若 $b_{n} = \frac{1}{4 a_{n} a_{n + 1}}$ ，数列 ${b_{n}}$ 的前n项和为 $T_{n}$ ，证明： $T_{n} < \frac{1}{2}$ ．

查看试题解析
18. 在① $\frac{s i n C}{s i n A + s i n B} + \frac{b}{a + c} = 1$ ， ② $c c o s C s i n A = (2 b - c) s i n C c o s A$ 这两个条件中任选一个，补充到下面横线上，并解答．
记△ABC的内角A，B，C的对边分别为a，b，c，且____．
（注：如果选择多个条件分别解答，则按第一个解答计分．）

(1)、求 $∠ A$ ；

(2)、若 $| \vec{C B} - \vec{C A} | = 4$ ， $c o s B + c o s C = 1$ ，求△ABC的面积．

查看试题解析
19. 如图，在多面体ABCDEF中，A，B，C，D四点共面， $A B = A C = A F = C E 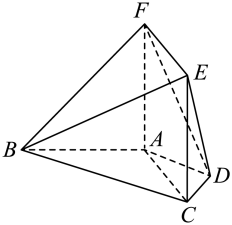= 2$ ， $A F ∥ C E$ ， AF⊥平面ABCD， $D E^{2} + D F^{2} = 12$ ．

(1)、求证：CD⊥平面ADF；

(2)、若 $A D = C D$ ， $A B ⊥ A C$ ，求平面 $B E F$ 和平面 $D E F$ 的夹角的余弦值．

查看试题解析
20. 在某校举办“青春献礼二十大，强国有我新征程”的知识能力测评中，随机抽查了100名学生，其中共有4名女生和3名男生的成绩在90分以上，从这7名同学中每次随机抽1人在全校作经验分享，每位同学最多分享一次，记第一次抽到女生为事件A，第二次抽到男生为事件B．

(1)、求 $P (B)$ ， $P (B | A)$ ，

(2)、若把抽取学生的方式更改为：从这7名学生中随机抽取3人进行经验分享，记被抽取的3人中女生的人数为X，求X的分布列和数学期望．

查看试题解析
21. 已知P为抛物线E： $y^{2} = 2 p x (p > 0)$ 上任意一点，过点P作 $P Q ⊥ y$ 轴，垂足为O，点 $C (7 ， 8)$ 在抛物线上方（如图所示），且 $| P C | + | P Q |$ 的最小值为9．

(1)、求E的方程；

(2)、若直线 $y = x + m (m \neq 0)$ 与抛物线E相交于不同的两点A，B，线段AB的垂直平分线交x轴于点N，且 $△ A B N$ 为等边三角形，求m的值．

查看试题解析
22. 已知函数 $f (x) = a l n x - \frac{a^{2}}{x} - x (a > 0)$ ，曲线 $y = f (x)$ 在点 $(1 ， f (1))$ 处的切线与直线 $x - y + 1 = 0$ 平行．

(1)、求a的值；

(2)、若 $x \in [1 ， + ∞)$ 时，不等式 $f (x) ≤ (m - 1) x - \frac{(m + 1)}{x}$ 恒成立，求实数m的取值范围．

查看试题解析