云南省大理、丽江2023届高三数学毕业生第二次复习统一检测试卷
试卷更新日期:2023-03-10 类型:高考模拟
一、单选题
-
1. 设集合 , 则( )A、 B、 C、 D、2. 已知为虚数单位,复数的共轭复数为 , 则( )A、 B、 C、 D、3. 若平面向量与的夹角为60°, , , 则等于( ).A、 B、 C、4 D、124. 《九章算术》是我国古代的数学巨著,书中有这样一道题:“今有垣厚五尺,两鼠对穿.大鼠日一尺,小鼠亦日一尺,大鼠日自倍,小鼠日自半.问何日相逢?”题意为:有一堵墙厚五尺,有两只老鼠从墙的正对面打洞穿墙.大老鼠第一天打进一尺,以后每天打进的长度是前一天的2倍;小老鼠第一天也打进一尺,以后每天打进的长度是前一天的一半.若这一堵墙厚 尺,则几日后两鼠相逢( )A、3 B、4 C、5 D、65. 中国南北朝时期数学家、天文学家祖冲之、祖暅父子总结了魏晋时期著名数学家刘徽的有关工作,提出“幂势既同,则积不容异”.“幂”是截面积,“势”是几何体的高.详细点说就是,界于两个平行平面之间的两个几何体,被任一平行于这两个平面的平面所截,如果两个截面的面积相等,则这两个几何体的体积相等.上述原理在中国被称为祖暅原理.一个上底面边长为1,下底面边长为2,高为 的正六棱台与一个不规则几何体满足“幂势既同”,则该不规则几何体的体积为( )
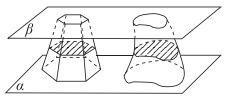 A、16 B、 C、 D、216. 抛物线有如下光学性质:过焦点的光线经抛物线反射后得到的光线平行于抛物线的对称轴;反之,平行于抛物线对称轴的入射光线经抛物线反射后必过抛物线的焦点.已知抛物线 的焦点为F,一条平行于x轴的光线从点 射出,经过抛物线上的点A反射后,再经抛物线上的另一点B射出,则 的周长为( )A、 B、 C、 D、7. 已知实数a、b、c满足 , 则a、b、c的大小关系为( )A、 B、 C、 D、8. 已知函数 , 是函数的一个零点,是函数的一条对称轴,若在区间上单调,则的最大值是( )A、14 B、16 C、18 D、20
A、16 B、 C、 D、216. 抛物线有如下光学性质:过焦点的光线经抛物线反射后得到的光线平行于抛物线的对称轴;反之,平行于抛物线对称轴的入射光线经抛物线反射后必过抛物线的焦点.已知抛物线 的焦点为F,一条平行于x轴的光线从点 射出,经过抛物线上的点A反射后,再经抛物线上的另一点B射出,则 的周长为( )A、 B、 C、 D、7. 已知实数a、b、c满足 , 则a、b、c的大小关系为( )A、 B、 C、 D、8. 已知函数 , 是函数的一个零点,是函数的一条对称轴,若在区间上单调,则的最大值是( )A、14 B、16 C、18 D、20二、多选题
-
9. 在的展开式中,下列说法正确的是( )A、不存在常数项 B、二项式系数和为1 C、第4项和第5项二项式系数最大 D、所有项的系数和为12810. 如图,在正方体中,E、F、G分别为的中点,则( )
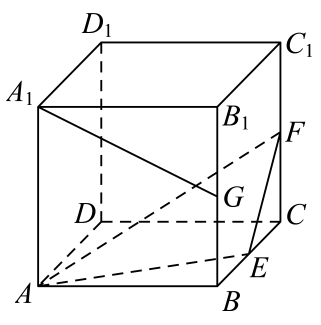 A、 B、与所成角为 C、 D、平面11. 在平面直角坐标系中,动点P与两个定点和连线的斜率之积等于 , 记点P的轨迹为曲线E,则( )A、E的方程为 B、E的离心率为 C、E的渐近线与圆相切 D、过点作曲线E的切线仅有2条12. 已知定义在R上的函数 , 对于任意的 恒有 , 且 , 若存在正数t,使得 , 则下列结论正确的是( )A、 B、 C、为偶函数 D、为周期函数
A、 B、与所成角为 C、 D、平面11. 在平面直角坐标系中,动点P与两个定点和连线的斜率之积等于 , 记点P的轨迹为曲线E,则( )A、E的方程为 B、E的离心率为 C、E的渐近线与圆相切 D、过点作曲线E的切线仅有2条12. 已知定义在R上的函数 , 对于任意的 恒有 , 且 , 若存在正数t,使得 , 则下列结论正确的是( )A、 B、 C、为偶函数 D、为周期函数三、填空题
-
13. “幸福感指数”是指某个人主观地评价他对自己的前生活状态的满意程度的指标,常用区间[0,10]内的一个数来表示,该数越接近10,表示满意度越高.现随机抽取10位某市市民,他们的幸福感指数为4,4,5,5,6,7,7,8,9,10.则这组数据的第80百分位数是 .14. 已知直线 , 圆 , 则圆关于直线对称的圆的方程为.15. 若曲线有两条过坐标原点的切线,则实数a的取值范围为.16. 把半椭圆: 和圆弧: 合成的曲线称为“曲圆”,其中点 是半椭圆的右焦点, 分别是“曲圆”与 轴的左、右交点, 分别是“曲圆”与 轴的上、下交点,已知 ,过点 的直线与“曲圆”交于 两点,则半椭圆方程为( ), 的周长的取值范围是.
四、解答题
-
17. 已知等差数列和等比数列满足 , , , .(1)、求和的通项公式;(2)、数列和中的所有项分别构成集合 , , 将的所有元素按从小到大依次排列构成一个新数列 , 求数列的前60项和.18. 在如图所示的几何体中,四边形是正方形,四边形是梯形, , , 平面平面 , 且.
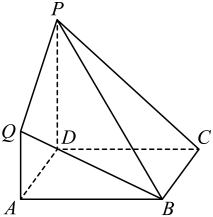 (1)、证明:平面平面;(2)、求平面与平面夹角的大小.19. 在① ,② ,③ 三个条件中选一个,补充在下面的横线处,然后解答问题.在 中,角 , , 所对的边分别是 , , ,设 的面积为 ,已知________.(1)、求角 的值;(2)、若 ,点 在边 上, 为 的平分线, 的面积为 ,求边长 的值.20. 党的二十大胜利召开后,某校为调查性别因素对党史知识的了解情况是否有影响,随机抽查了男女教职工各100名,得到如下数据:
(1)、证明:平面平面;(2)、求平面与平面夹角的大小.19. 在① ,② ,③ 三个条件中选一个,补充在下面的横线处,然后解答问题.在 中,角 , , 所对的边分别是 , , ,设 的面积为 ,已知________.(1)、求角 的值;(2)、若 ,点 在边 上, 为 的平分线, 的面积为 ,求边长 的值.20. 党的二十大胜利召开后,某校为调查性别因素对党史知识的了解情况是否有影响,随机抽查了男女教职工各100名,得到如下数据:不了解
了解
女职工
30
70
男职工
20
80
附:
0.010
0.005
0.001
6.635
7.879
10.828
(1)、根据小概率值的独立性检验,能否认为对党史知识的了解情况与性别有关?(2)、为了增进全体教职工对党史知识的了解,该校组织开展党史知识竞赛活动并以支部为单位参加比赛现有两组党史题目放在甲、乙两个纸箱中,甲箱有5个选择题和3个填空题,乙箱中有4个选择题和3个填空题,比赛中要求每个支部在甲或乙两个纸箱中随机抽取两题作答.每个支部先抽取一题作答,答完后题目不放回纸箱中,再抽取第二题作答,两题答题结束后,再将这两个题目放回原纸箱中,若第一支部从甲箱中抽取了2个题目,答题结束后错将题目放入了乙箱中,接着第二支部答题,第二支部抽取第一题时,从乙箱中抽取了题目.已知第二支部从乙箱中取出的这个题目是选择题,求第一支部从甲箱中取出的是2个选择题的概率.