上海市黄浦区2023届高三上学期数学一模试卷
试卷更新日期:2023-03-10 类型:高考模拟
一、填空题
-
1. 函数的定义域是 .2. 已知集合 , , 则.3. 在 的二项展开式中, 的系数是
4. 已知向量 , , 若 , 则mn的值为.5. 已知复数满足(为虚数单位),则复数的模等于.6. 某个品种的小麦麦穗长度(单位:cm)的样本数据如下:10.2、9.7、10.8、9.1、8.9、8.6、9.8、9.6、9.9、11.2、10.6、11.7,则这组数据的第80百分位数为.7. 在平面直角坐标系中,若角的顶点为坐标原点,始边与x轴的非负半轴重合,终边与以点O为圆心的单位圆交于点 , 则的值为.8. 若一个圆锥的侧面展开图是面积为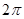 的半圆面,则该圆锥的体积为. 9. 已知的三边长分别为4、5、7,记的三个内角的正切值所组成的集合为 , 则集合中的最大元素为.10. 现有5人参加抽奖活动,每人依次从装有5张奖票(其中3张为中奖票)的箱子中不放回地随机抽取一张,直到3张中奖票都被抽出时活动结束,则活动恰好在第4人抽完后结束的概率为 .11. 已知四边形ABCD是平行四边形,若 , , , 且 , 则在上的数量投影为.12. 已知曲线与曲线 , 长度为1的线段AB的两端点A、B分别在曲线、上沿顺时针方向运动,若点A从点开始运动,点B到达点时停止运动,则线段AB所扫过的区域的面积为.
的半圆面,则该圆锥的体积为. 9. 已知的三边长分别为4、5、7,记的三个内角的正切值所组成的集合为 , 则集合中的最大元素为.10. 现有5人参加抽奖活动,每人依次从装有5张奖票(其中3张为中奖票)的箱子中不放回地随机抽取一张,直到3张中奖票都被抽出时活动结束,则活动恰好在第4人抽完后结束的概率为 .11. 已知四边形ABCD是平行四边形,若 , , , 且 , 则在上的数量投影为.12. 已知曲线与曲线 , 长度为1的线段AB的两端点A、B分别在曲线、上沿顺时针方向运动,若点A从点开始运动,点B到达点时停止运动,则线段AB所扫过的区域的面积为.二、单选题
-
13. 在平面直角坐标系中,“”是“方程表示的曲线是双曲线”的( )条件A、充分不必要 B、必要不充分 C、充要 D、既不充分也不必要14. 如图,四边形ABCD是边长为1的正方形,平面ABCD,平面ABCD,且 , 点G为MC的中点.则下列结论中不正确的是( )
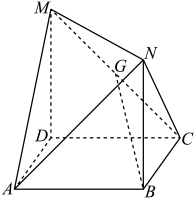 A、 B、平面平面ABN C、直线GB与AM是异面直线 D、直线GB与平面AMD无公共点15. 已知 , 且函数恰有两个极大值点在 , 则的取值范围是( )A、 B、 C、 D、16. 设a、b、c、p为实数,若同时满足不等式、与的全体实数x所组成的集合等于.则关于结论:①a、b、c至少有一个为0;②.下列判断中正确的是( )A、①和②都正确 B、①和②都错误 C、①正确,②错误 D、①错误,②正确
A、 B、平面平面ABN C、直线GB与AM是异面直线 D、直线GB与平面AMD无公共点15. 已知 , 且函数恰有两个极大值点在 , 则的取值范围是( )A、 B、 C、 D、16. 设a、b、c、p为实数,若同时满足不等式、与的全体实数x所组成的集合等于.则关于结论:①a、b、c至少有一个为0;②.下列判断中正确的是( )A、①和②都正确 B、①和②都错误 C、①正确,②错误 D、①错误,②正确三、解答题
-
17. 已知是等差数列,是等比数列,且 , , , .(1)、求的通项公式;(2)、设 , 求数列的前2n项和.18. 如图所示,四棱锥 中,底面 为菱形,且直线 又棱 为 的中点,
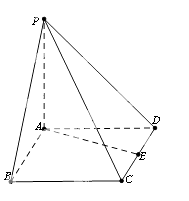
(Ⅰ) 求证:直线 ;
(Ⅱ) 求直线 与平面 的正切值.
19. 某展览会有四个展馆,分别位于矩形ABCD的四个顶点A、B、C、D处,现要修建如图中实线所示的步道(宽度忽略不计,长度可变)把这四个展馆连在一起,其中百米,百米,且.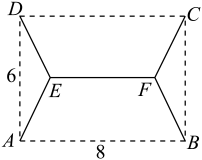 (1)、试从各段步道的长度与图中各角的弧度数中选择某一变量作为自变量x,并求出步道的总长y(单位:百米)关于x的函数关系式;(2)、求步道的最短总长度(精确到0.01百米).20. 已知椭圆的离心率为 , 以其四个顶点为顶点的四边形的面积等于.动直线、都过点 , 斜率分别为k、 , 与椭圆C交于点A、P,与椭圆C交于点B、Q,点P、Q分别在第一、四象限且轴.
(1)、试从各段步道的长度与图中各角的弧度数中选择某一变量作为自变量x,并求出步道的总长y(单位:百米)关于x的函数关系式;(2)、求步道的最短总长度(精确到0.01百米).20. 已知椭圆的离心率为 , 以其四个顶点为顶点的四边形的面积等于.动直线、都过点 , 斜率分别为k、 , 与椭圆C交于点A、P,与椭圆C交于点B、Q,点P、Q分别在第一、四象限且轴.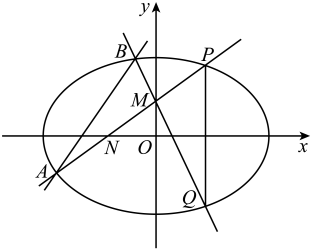 (1)、求椭圆C的标准方程;(2)、若直线与x轴交于点N,求证:;(3)、求直线AB的斜率的最小值,并求直线AB的斜率取最小值时的直线的方程.21. 已知集合A和定义域为的函数 , 若对任意 , , 都有 , 则称是关于A的同变函数.(1)、当与时,分别判断是否为关于A的同变函数,并说明理由;(2)、若是关于的同变函数,且当时, , 试求在上的表达式,并比较与的大小;(3)、若n为正整数,且是关于的同变函数,求证:既是关于的同变函数,也是关于的同变函数.
(1)、求椭圆C的标准方程;(2)、若直线与x轴交于点N,求证:;(3)、求直线AB的斜率的最小值,并求直线AB的斜率取最小值时的直线的方程.21. 已知集合A和定义域为的函数 , 若对任意 , , 都有 , 则称是关于A的同变函数.(1)、当与时,分别判断是否为关于A的同变函数,并说明理由;(2)、若是关于的同变函数,且当时, , 试求在上的表达式,并比较与的大小;(3)、若n为正整数,且是关于的同变函数,求证:既是关于的同变函数,也是关于的同变函数.