陕西省西安市长安区2023届高三下学期理数一模试卷

试卷更新日期：2023-03-10 类型：高考模拟

进入出卷网下载

一、单选题

1. 设集合 $A = {x | 0 < x \leq 4 ， x \in N} ， B = {x | 2^{x} \leq 6}$ ，则 $A ∩ B =$ （）

A、 ${1 ， 2}$ B、 $[1 ， 2]$ C、 ${1 ， 2 ， 3}$ D、 $[1 ， 3]$

查看试题解析
2. 甲乙两位射击运动员参加比赛，抽取连续6轮射击比赛的成绩情况如下：
甲：80、70、80、90、90、70；乙：70、80、80、80、70、80
则下列说法中正确的是（）

A、甲比乙平均成绩高，甲比乙成绩稳定 B、甲比乙平均成绩高，乙比甲成绩稳定 C、乙比甲平均成绩高，甲比乙成绩稳定 D、乙比甲平均成绩高，乙比甲成绩稳定

查看试题解析
3. 复数 $z$ 满足 $z^{3} = - 2 + 2 i$ ，则 $z =$ （）

A、 $1 - i$ B、 $1 + i$ C、 $- 1 - i$ D、 $- 1 + i$

查看试题解析
4. 函数 $f (x) = \frac{1 0^{x} - 1}{1 0^{x} + 1} \cdot s i n x$ 在区间 $[- \frac{π}{2} ， \frac{π}{2}]$ 上的图象大致为（）

A、 B、 C、 D、

查看试题解析
5. 在平行四边形ABCD中， $\vec{A E} = \frac{1}{3} \vec{A D}$ ， $\vec{C F} = \frac{1}{3} \vec{C D}$ ，则 $\vec{B A} =$ （）

A、 $\frac{6}{5} \vec{A F} - \frac{9}{5} \vec{C E}$ B、 $\frac{2}{5} \vec{A F} - \frac{3}{5} \vec{C E}$ C、 $\frac{6}{5} \vec{A F} + \frac{9}{5} \vec{C E}$ D、 $\frac{2}{5} \vec{A F} + \frac{3}{5} \vec{C E}$

查看试题解析
6. 我国古代数学家僧一行应用“九服晷影算法”在《大衍历》中建立了晷影长1与太阳天顶距 $θ (0 ° \leq θ \leq 180 °)$ 的对应数表，这是世界数学史上较早的一张正切函数表，根据三角学知识可知，晷影长度l等于表高h与太阳天顶距 $θ$ 正切值的乘积，即 $l = h t a n θ$ ．对同一“表高”两次测量，第一次和第二次太阳天顶距分别为 $α ， β$ ，且 $t a n (α - β) = \frac{1}{3}$ ，若第二次的“晷影长”与“表高”相等，则第一次的“晷影长”是“表高”的（）

A、1倍 B、2倍 C、3倍 D、4倍

查看试题解析
7. 下列是函数 $f (x) = 2 s i n (x + \frac{3 π}{4}) s i n (x + \frac{π}{4})$ 图像的对称轴的是（）

A、 $x = \frac{π}{6}$ B、 $x = \frac{π}{4}$ C、 $x = \frac{π}{3}$ D、 $x = \frac{π}{2}$

查看试题解析
8. 盲盒是一种深受大众喜爱的玩具，某盲盒生产厂商准备将棱长为 $8 c m$ 的正四面体的魔方放入正方体盲盒内，为节约成本，使得魔方能够放入盲盒且盲盒棱长最小时，盲盒内剩余空间的体积为（）

A、 $\frac{64 \sqrt{2}}{3} c m^{3}$ B、 $\frac{128 \sqrt{2}}{3} c m^{3}$ C、 $\frac{256 \sqrt{2}}{3} c m^{3}$ D、 $\frac{512 \sqrt{2}}{3} c m^{3}$

查看试题解析
9. 已知点 $F (4 ， 0)$ 是双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的右焦点，过点F向C的一条渐近线引垂线垂足为A，交另一条渐近线于点B．若 $2 \vec{A F} = \vec{F B}$ ，则双曲线C的方程为（）

A、 $\frac{x^{2}}{12} - \frac{y^{2}}{4} = 1$ B、 $\frac{x^{2}}{4} - \frac{y^{2}}{12} = 1$ C、 $\frac{x^{2}}{10} - \frac{y^{2}}{6} = 1$ D、 $\frac{x^{2}}{6} - \frac{y^{2}}{10} = 1$

查看试题解析
10. 已知函数 $f (x)$ 满足 $2 f (x) + f (- x) = - 2 x$ ，若 $2^{a} = l o g_{2} b = c$ ，则（）

A、 $f (a) < f (b) < f (c)$ B、 $f (b) < f (c) < f (a)$ C、 $f (a) < f (c) < f (b)$ D、 $f (c) < f (b) < f (a)$

查看试题解析
11. 在三棱锥 $A - B C D$ 中，平面 $A C D ⊥$ 平面BCD， $△ A C D$ 是以CD为斜边的等腰直角三角形，M为CD中点， $B M ⊥ B C$ ， $A C = 2 B C = 4$ ，则该三棱锥的外接球的表面积为（）

A、 $16 π$ B、 $24 π$ C、 $32 π$ D、 $40 π$

查看试题解析
12. 设函数 $f (x)$ 的定义域为 $R$ ，满足 $f (x + 2) = 2 f (x)$ ，且当 $x \in (0 ， 2]$ 时， $f (x) = x (2 - x)$ .则下列结论正确的个数是（）
① $f (7) = 8$ ；②若对任意 $x \in (- \infty ， m]$ ，都有 $f (x) \leq 6$ ，则 $m$ 的取值范围是 $(- \infty ， \frac{13}{2}]$ ；③若方程 $f (x) = m (x - 5)$ 恰有3个实数根，则 $m$ 的取值范围是 $(- 1 ， - \frac{1}{4})$ ；④函数 $f (x)$ 在区间 $[2 n - 2 ， 2 n] (n \in N_{+})$ 上的最大值为 $a_{n}$ ，若 $\exists n \in N_{+}$ ，使得 $λ a_{n} < 2 n - 7$ 成立，则 $λ \in (- \infty ， \frac{3}{16}]$ .

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 设a为实数，函数 $f (x) = e^{x} - e^{- x} + a x^{2}$ 的导函数为 $f^{^{'}} (x)$ ，若 $f^{^{'}} (x)$ 是偶函数，则 $a =$ ，此时，曲线 $y = f (x)$ 在原点处的切线方程为．

查看试题解析
14. 已知直线 $l ： m x + y + \sqrt{3} m - 1 = 0$ 与圆 $x^{2} + y^{2} = 4$ 交于A，B两点，若 $| A B | = 2$ ，则 $m =$ ．

查看试题解析
15. 已知在 $△ A B C$ 中，角 $A ， B ， C$ 所对边分别为 $a ， b ， c$ ，满足 $2 b c o s A + a = 2 c$ ，且 $b = 2 \sqrt{3}$ ，则 $2 a - c$ 的取值范围为.

查看试题解析
16. 在生活中，可以利用如下图工具绘制椭圆，已知 $O$ 是滑杆上的一个定点，D可以在滑杆上自由移动，线段 $| O A | = | A D | = 3$ ，点E在线段 $A D$ 上，且满足 $\vec{A E} = λ \vec{E D}$ ，若点E所形成的椭圆的离心率为 $\frac{2 \sqrt{6}}{5}$ ，则 $λ =$ .

查看试题解析

三、解答题

17. 已知等差数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，满足 $a_{3} = 6$ ， ____．
在① $S_{3} = a_{6}$ ；② $S_{4} = 20$ ；③ $a_{2} + a_{5} + a_{8} = 30$ 这三个条件中任选一个，补充在上面的问题中并解答（注：如果选择多个条件，按照第一个解答给分．在答题前应说明“我选____”）

(1)、求 ${a_{n}}$ 的通项公式；

(2)、设 $b_{n} = 2^{a_{n}} + a_{n}$ ，求 ${b_{n}}$ 的前n项和 $T_{n}$ ．

查看试题解析
18. 如图，在四棱锥 $P - A B C D$ 中， $P A ⊥$ 平面 $A B C D$ ， $A D ⊥ C D$ ， $A D ∥ B C$ ， $P A = A D = C D = 2$ ， $B C = 3$ ， E为 $P D$ 的中点，F在 $P C$ 上，满足 $E F ⊥ P C$ .

(1)、求证： $C D ⊥$ 平面 $P A D$ ；

(2)、求二面角 $B - A F - C$ 的余弦值.

查看试题解析
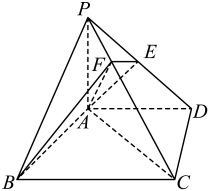19. 设抛物线 $C ：$ $y^{2} = 2 p x$ $(p > 0)$ 的焦点为 $F$ ， $M \in C$ ， Q在准线上，Q的纵坐标为 $\sqrt{3} p$ ，点M到F与到定点 $Q$ 的距离之和的最小值为4．

(1)、求抛物线C的方程；

(2)、过F且斜率为2的直线l与C交于A、B两点，求 $△ A B Q$ 的面积．

查看试题解析
20. 某学校组织知识竞答比赛，设计了两种答题方案：
方案一：先回答一道多选题，从第二道开始都回答单选题；
方案二：全部回答单选题.
其中每道单选题答对得2分，答错得0分；
多选题全部选对得3分，选对但不全得1分，有错误选项得0分.
每名参与竞答的同学至多答题3道.在答题过程中得到4分或4分以上立刻停止答题.统计参与竞答的500名同学，所得结果如下表所示：

男生
女生
选择方案一
100
80
选择方案二
200
120
附： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ， $n = a + b + c + d$ .
$P (K^{2} \geq k_{0})$
0.15
0.10
0.05
0.025
0.010
0.005
0.001
$k_{0}$
2.072
2.706
3.841
5.024
6.635
7.879
10.828

(1)、能否有90%的把握认为方案的选择与性别有关?

(2)、小明回答每道单选题的正确率为0.8；多选题完全选对的概率为0.3，选对且不全的概率为0.3.
①若小明选择方案一，记小明的得分为X，求X的分布列及数学期望；
②如果你是小明，为了获取更好的得分你会选择哪个方案?请通过计算说明理由.

查看试题解析
21. 已知函数 $f (x) = e^{x} - x^{2}$ ，求证：

(1)、 $f (x)$ 存在唯一零点；

(2)、不等式 $e^{x - 1} - x^{2} + x - 1 + (l n x)^{2} \geq 0$ 恒成立．

查看试题解析
22. 在直角坐标系 $x O y$ 中，曲线C的参数方程为 ${\begin{array}{l} x = \frac{t^{2}}{4} + \frac{1}{t^{2}} - 1 \\ y = \sqrt{3} t - \frac{2 \sqrt{3}}{t} \end{array}$ （ $t > 0$ ， t为参数）．

(1)、求曲线C的直角坐标方程；

(2)、已知直线 $l ： x - y - 1 = 0$ 与x轴的交点为F，且曲线C与直线l交于A、B两点，求 $| F A | \cdot | F B |$ 的值．

查看试题解析
23. 已知 $f (x) = | x - 1 | + | x - 3 |$ ．

(1)、求 $f (x) \leq 3$ 的解集；

(2)、已知 $a (x - 2)^{2} + 1 \geq f (x)$ 在 $[3 ， + \infty)$ 上恒成立，求实数a的取值范围．

查看试题解析

$P (K^{2} \geq k_{0})$	0.15	0.10	0.05	0.025	0.010	0.005	0.001
$k_{0}$	2.072	2.706	3.841	5.024	6.635	7.879	10.828

	男生	女生
选择方案一	100	80
选择方案二	200	120