云南省玉溪市峨山县2022年初中学业水平模拟考试数学试题(三模)
试卷更新日期:2023-03-10 类型:中考模拟
一、单选题
-
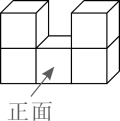
1. 如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图为( )
 A、
A、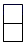 B、
B、 C、
C、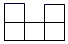 D、
D、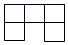 2. 2021年12月3日,全长1035公里、总投资约50 500 000 000元的中老铁路全线开通运营,它是以中方为主投资建设、全线采用中国技术标准、使用中国设备并与中国铁路网直接连通的国际铁路.数据50 500 000 000用科学记数法可表示为( )A、0.505×1011 B、505×108 C、5.05×1010 D、50.5×1093. 下列运算正确的是( )A、 B、 C、 D、4. 正九边形每一个内角的度数为( )A、120° B、130° C、140° D、150°5. 已知点在反比例函数的图象上,则下列各点在该函数图象上的是( )A、 B、 C、 D、6. 如图,在△ABC中,点D,E分别在边AB,AC上, , 且BC=6, , 则DE的长等于( )
2. 2021年12月3日,全长1035公里、总投资约50 500 000 000元的中老铁路全线开通运营,它是以中方为主投资建设、全线采用中国技术标准、使用中国设备并与中国铁路网直接连通的国际铁路.数据50 500 000 000用科学记数法可表示为( )A、0.505×1011 B、505×108 C、5.05×1010 D、50.5×1093. 下列运算正确的是( )A、 B、 C、 D、4. 正九边形每一个内角的度数为( )A、120° B、130° C、140° D、150°5. 已知点在反比例函数的图象上,则下列各点在该函数图象上的是( )A、 B、 C、 D、6. 如图,在△ABC中,点D,E分别在边AB,AC上, , 且BC=6, , 则DE的长等于( ) A、1.5 B、2 C、2.5 D、37. 关于x的一元二次方程的一个根是1,则另一个根是( )A、3 B、-2 C、-3 D、-48. 在Rt△ABC中,∠C=90°,AB=4,AC=2,则sinA的值为( )A、 B、 C、 D、9. 如图,AB是⊙O的直径,CD是⊙O的弦,连接AC,AD,BD.若∠CAB=36°,则∠ADC的度数为( )
A、1.5 B、2 C、2.5 D、37. 关于x的一元二次方程的一个根是1,则另一个根是( )A、3 B、-2 C、-3 D、-48. 在Rt△ABC中,∠C=90°,AB=4,AC=2,则sinA的值为( )A、 B、 C、 D、9. 如图,AB是⊙O的直径,CD是⊙O的弦,连接AC,AD,BD.若∠CAB=36°,则∠ADC的度数为( ) A、72° B、54° C、45° D、36°10. 某工厂计划生产300个零件,由于采用新技术,实际每天生产零件的数量是原计划的2倍,因此提前5天完成任务.设原计划每天生产零件x个,根据题意,所列方程正确的是( )A、 ﹣ =5 B、 ﹣ =5 C、 ﹣ =5 D、 ﹣ =511. 某公司今年1~4月的电子产品销售总额如图1所示,其中平板电脑的销售额占当月电子产品销售总额的百分比如图2,据图中信息,得到的结论不合理的是( )
A、72° B、54° C、45° D、36°10. 某工厂计划生产300个零件,由于采用新技术,实际每天生产零件的数量是原计划的2倍,因此提前5天完成任务.设原计划每天生产零件x个,根据题意,所列方程正确的是( )A、 ﹣ =5 B、 ﹣ =5 C、 ﹣ =5 D、 ﹣ =511. 某公司今年1~4月的电子产品销售总额如图1所示,其中平板电脑的销售额占当月电子产品销售总额的百分比如图2,据图中信息,得到的结论不合理的是( ) A、这4个月,电子产品销售总额为290万元 B、平板电脑销售额占当月电子产品销售总额的百分比,1月最高 C、这4个月,平板电脑销售额最低的是3月 D、平板电脑4月份的销售额比3月份有所下降12. 已知关于x、y的方程组 的解为整数,且关于x的不等式组 有且仅有5个整数解,则所有满足条件的整数a的和为( )A、﹣1 B、﹣2 C、﹣8 D、﹣6
A、这4个月,电子产品销售总额为290万元 B、平板电脑销售额占当月电子产品销售总额的百分比,1月最高 C、这4个月,平板电脑销售额最低的是3月 D、平板电脑4月份的销售额比3月份有所下降12. 已知关于x、y的方程组 的解为整数,且关于x的不等式组 有且仅有5个整数解,则所有满足条件的整数a的和为( )A、﹣1 B、﹣2 C、﹣8 D、﹣6二、填空题
-
13. 函数y= 中,自变量x的取值范围是 .14. 如图,直线a、b、c、d,已知c⊥a,c⊥b,直线b、c、d交于一点,若∠1=50°,则∠2=°.
 15. 分解因式: =16. 观察下列各等式: , , , …,根据你发现的规律计算:=(n为正整数).17. 如图,在边长为2的正方形ABCD中,对角线AC的中点为O,分别以点A,C为圆心,以AO的长为半径画弧,分别与正方形的边相交,则图中的阴影部分的面积为.(结果保留π)
15. 分解因式: =16. 观察下列各等式: , , , …,根据你发现的规律计算:=(n为正整数).17. 如图,在边长为2的正方形ABCD中,对角线AC的中点为O,分别以点A,C为圆心,以AO的长为半径画弧,分别与正方形的边相交,则图中的阴影部分的面积为.(结果保留π)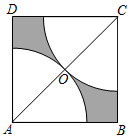 18. 在直角边分别为6cm和8cm的直角三角形中作菱形,使菱形的一个内角恰好是三角形的一个角,其余顶点都在三角形的边上,则所作菱形的边长是 .
18. 在直角边分别为6cm和8cm的直角三角形中作菱形,使菱形的一个内角恰好是三角形的一个角,其余顶点都在三角形的边上,则所作菱形的边长是 .三、解答题
-
19. 重庆市2022年体育中考将在3月底4月初进行,近日,某中学初三年级组织了一次体育中考模拟测试.现从该校初三年级男女生中各抽取10名同学的成绩进行统计分析(成绩得分用x表示,共分成四组:A:30≤x<35,B:35≤x<40,C:40≤x<45,D:45≤x≤50),绘制了如下的图表,请根据图中的信.息解答下列问题,
10名男生的成绩是:32,34,38,43,44,45,47,48,50,50
10名女生的成绩在C组中的数据是:43,44,44
男生、女生抽取学生测试成绩统计表

年级
平均数
中位数
众数
D组占比
男生
43.1
44.5
b
c
女生
43.1
a
44
40%
(1)、直接写出上表中a,b,c的值;(2)、根据以上数据,你认为该校初三年级男生和女生谁的体育成绩更好?请说明理由;(写出一条理由即可)(3)、若该校初三年级共有400人参加了此次测试,估计参加此次测试成绩优秀(45≤x≤50)的学生共有多少人?20. 为纪念历史,缅怀先烈,某校社团将电影《长津湖》中的四位历史英雄人物头像制成编号为 A、B、C、D 的四张卡片(除编号和头像外其余完全相同),活动时学生根据所抽取的卡片来讲述他们在影片中的历史事迹.规则如下:先将四张卡片背面朝上,洗匀放好,小强从中随机抽取一张,然后放回并洗匀,小叶再从中随机抽取一张. (1)、小强从中随机抽取一张卡片是“伍千里”的概率是 .(2)、请用列表或画树状图的方法求小强和小叶抽到的两张卡片恰好是同一英雄人物的概率.21. 如图,平行四边形ABCD的对角线 AC,BD 交于点 O,AE⊥BC于点 E,点F在BC延长线上,且CF=BE.
(1)、小强从中随机抽取一张卡片是“伍千里”的概率是 .(2)、请用列表或画树状图的方法求小强和小叶抽到的两张卡片恰好是同一英雄人物的概率.21. 如图,平行四边形ABCD的对角线 AC,BD 交于点 O,AE⊥BC于点 E,点F在BC延长线上,且CF=BE. (1)、求证:四边形 AEFD 是矩形;(2)、连接 AF,若 , BE=1,AD=3,求AF的长.22. 某剧院举行专场音乐会,成人票每张20元,学生票每张5元.暑假期间,为了丰富广大师生的业余文化生活,该剧院制定了两种优惠方案.
(1)、求证:四边形 AEFD 是矩形;(2)、连接 AF,若 , BE=1,AD=3,求AF的长.22. 某剧院举行专场音乐会,成人票每张20元,学生票每张5元.暑假期间,为了丰富广大师生的业余文化生活,该剧院制定了两种优惠方案.方案一:购买一张成人票赠送一张学生票;
方案二:按总价的90%付款.
某校有4名老师带队,与若干名(不少于4人)学生一起听音乐会.设学生人数为x(x≥4且x为整数).方案一付款总金额为y1元,方案二付款总金额为y2元,
(1)、分别求y1 , y2关于x的函数表达式;(2)、①若用两种方案购买音乐会门票的花费相同,求听音乐会的学生人数;②若购买音乐会门票共花费了450元,要使听音乐会的学生人数最多,应该用哪个方案购买音乐会门票?
