云南省普洱市2022年中考数学二模试题

试卷更新日期：2023-03-10 类型：中考模拟

进入出卷网下载

一、单选题

1. $- \frac{1}{2}$ 的倒数是（）

A、-2 B、2 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 移动互联网已经全面进入人们的日常生活.截止2015年3月，全国4G用户总数达到1.62亿，其中1.62亿用科学记数法表示为（）

A、1.62×10⁴ B、1.62×10⁶ C、1.62×10⁸ D、0.162×10⁹

查看试题解析
3. 如图是某几何体的三视图，该几何体是（）

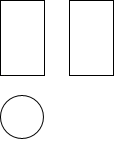A、圆柱 B、正方体 C、圆锥 D、球

查看试题解析
4. 圆锥的母线长为4，底面半径为2，则此圆锥的侧面积是（）

A、 $16 π$ B、 $12 π$ C、 $8 π$ D、 $6 π$

查看试题解析
5. 如图，△ABD的三个顶点在⊙O上，AB是直径，点C在⊙O上，且∠ABD＝52°，则∠BCD等于（　　）

A、32° B、38° C、52° D、66°

查看试题解析
6. 下列运算正确的是（　　）

A、4ab÷2a=2ab B、（3x²）³=9x⁶ C、a³•a⁴=a⁷ D、 $\sqrt{6}$ ÷ $\sqrt{3}$ =2

查看试题解析
7. 一元二次方程 ${2x}^{2} - 5x + 1 = 0$ 的根的情况是

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定

查看试题解析
8. 在同一直角坐标系中，函数y＝kx+1与y＝﹣ $\frac{k}{x}$ （k≠0）的图象大致是（　　）

A、 B、 C、 D、

查看试题解析

二、填空题

9. 若式子 $\sqrt{x - 3}$ 有意义，则实数 $x$ 的取值范围是.

查看试题解析
10. 我市测得一周 $P M_{2.5}$ 的日均值 $($ 单位：微克 $/$ 立方米 $)$ 如下： $50$ ， $40$ ， $75$ ， $50$ ， $37$ ， $50$ ， $40$ ，这组数据的中位数和众数分别是．

查看试题解析
11. 分解因式：m³n−4mn=

查看试题解析
12. 若一个多边形的内角和是其外角和的3倍，则这个多边形的边数是．

查看试题解析
13. 把一张矩形纸片ABCD按如图方式折叠，使顶点B和顶点D重合，折痕为EF，若BF＝4，FC＝2，则△DEF的周长是．

查看试题解析
14. 如图在坐标系中放置一菱形OABC，已知∠ABC=60°，OA=1.先将菱形OABC沿x轴的正方向无滑动翻转，每次翻转60°，连续翻转2016次，点B的落点依次为B₁ ， B₂ ， B₃ ， …，则B₂₀₁₆的坐标为.

查看试题解析

三、解答题

15. 如图所示，正方形网格中，△ABC为格点三角形（即三角形的顶点都在格点上）.

（ 1 ）把△ABC沿BA方向平移后，点A移到点A₁ ，在网格中画出平移后得到的△A₁B₁C₁；

（ 2 ）把△A₁B₁C₁绕点A₁按逆时针方向旋转90°，在网格中画出旋转后的△A₁B₂C₂；

（ 3 ）如果网格中小正方形的边长为1，求点B经过（1）、（2）变换的路径总长.

查看试题解析
16. 计算：(－1)²－|－7|＋ $\sqrt{4}$ ×(2016－π)⁰＋( $\frac{1}{3}$ )^－1 ．

查看试题解析
17. 先化简，再求代数式( $\frac{1}{x - y}$ － $\frac{2}{x^{2} - x y}$ )÷ $\frac{x - 2}{3 x}$ 的值，其中x＝2＋ $\sqrt{3}$ ， y＝2．

查看试题解析
18. 如图，△ABC和△EFD分别在线段AE的两侧，点C，D在线段AE上，AC=DE，AB=EF，AB∥EF.
求证：BC=FD

查看试题解析
19.
某超市计划在“十周年”庆典当天开展购物抽奖活动，凡当天在该超市购物的顾客，均有一次抽奖的机会，抽奖规则如下：将如图所示的圆形转盘平均分成四个扇形，分别标上1，2，3，4四个数字，抽奖者连续转动转盘两次，当每次转盘停止后指针所指扇形内的数为每次所得的数（若指针指在分界线时重转）；当两次所得数字之和为8时，返现金20元；当两次所得数字之和为7时，返现金15元；当两次所得数字之和为6时返现金10元．

(1)、试用树状图或列表的方法表示出一次抽奖所有可能出现的结果

(2)、某顾客参加一次抽奖，能获得返还现金的概率是多少？

查看试题解析
20. 目前我市“校园手机”现象越来越受到社会关注，针对这种现象，随机抽查了某中学九年级的同学，关于手机在中学生中的主要用途做了调查，对调查数据进行统计整理、制作了如下的两种统计图，请根据图形回答问题：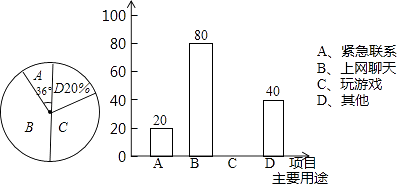

(1)、这次被调查的学生共有人，其中主要用于“上网聊天”的学生人数占抽样人数的百分比为；

(2)、请你将条形统计图（2）补充完整；

(3)、若该校共有3000名学生，请你估计主要使用手机玩游戏的人数大约有多少人？

查看试题解析
21.
如图，我国的一艘海监船在钓鱼岛A附近沿正东方向航行，船在B点时测得钓鱼岛A在船的北偏东60°方向，船以50海里/时的速度继续航行2小时后到达C点，此时钓鱼岛A在船的北偏东30°方向．请问船继续航行多少海里与钓鱼岛A的距离最近？

查看试题解析
22. 如图，点B、C、D都在⊙O上，过C点作CA∥BD交OD的延长线于点A，连接BC，∠B=∠A=30°， $B D = 2 \sqrt{3}$ ．

(1)、试说明：AC是⊙O的切线；

(2)、求由线段AC、AD与弧CD所围成的阴影部分的面积．（结果保留π）

查看试题解析
23. 如图，已知抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的对称轴为直线 $x = - 1$ ，且抛物线与 $x$ 轴交于 $A$ 、 $B$ 两点，与 $y$ 轴交于 $C$ 点，其中 $A (1 ， 0)$ ， $C (0 ， 3)$ .

(1)、若直线 $y = m x + n$ 经过 $B$ 、 $C$ 两点，求直线 $B C$ 和抛物线的解析式；

(2)、在抛物线的对称轴 $x = - 1$ 上找一点 $M$ ，使点 $M$ 到点 $A$ 的距离与到点 $C$ 的距离之和最小，求出点 $M$ 的坐标；

(3)、设点 $P$ 为抛物线的对称轴 $x = - 1$ 上的一个动点，求使 $Δ B P C$ 为直角三角形的点 $P$ 的坐标.

查看试题解析