云南省楚雄州2022年中考数学模拟预测试卷

试卷更新日期：2023-03-10 类型：中考模拟

进入出卷网下载

一、单选题

1. 比较m与2m的大小关系（）

A、 $m < 2 m$ B、 $m > 2 m$ C、 $m = 2 m$ D、以上都有可能

查看试题解析
2. 如图是由三个小正方体叠成的一个几何体，它的左视图是（）．

A、 B、 C、 D、

查看试题解析
3. 第24届冬季奥林匹克运动会于2022年2月4日在北京开幕.2022年北京冬奥会会徽以汉字“冬”为灵感来源；北京冬奥会的吉祥物“冰墩墩”是以熊猫为原型进行设计创作；北京冬季残奥会的吉祥物“雪容融”是以灯笼为原型进行设计创作．下列冬奥元素图片中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 5个整数从小到大的排列，其中位数是4，如果这组数据的唯一众数是6，则这5个整数最大的和可能是（）

A、 21 B、22 C、23 D、24

查看试题解析
5. 如果关于x的一元二次方程 $a x^{2} + b x + c = 0$ 有两个实数根，且其中一个根为另一个根的2倍，则称这样的方程为“倍根方程”，下列说法：
①方程 $x^{2} - 2 x - 8 = 0$ 是倍根方程；
②若 $(x - 2) (m x + n) = 0$ 是倍根方程，则 $m = - n$ 或 $m = - \frac{1}{4} n$ ；
③若方程 $a x^{2} + b x + c = 0$ 是倍根方程，且相异两点 $M (2 + t ， s)$ ， $N (4 - t ， s)$ 都在抛物线 $y = a x^{2} + b x + c$ 上，则方程 $a x^{2} + b x + c = 0$ 的一个根为2．
其中，正确说法的个数是（　　）

A、 $0$ B、 $1$ C、 $2$ D、 $3$

查看试题解析
6. 下列运算正确的是（　　）

A、 $x^{3} + x^{3} = 2 x^{6}$ B、 $x \cdot x^{2} = x^{3}$ C、 $(- x^{3})^{2} = - x^{6}$ D、 $x^{6} \div x^{3} = x^{2}$

查看试题解析
7. 在下列说法中，正确的有（　　）
①两点确定一条直线；
②过一点有且只有一条直线与已知直线平行；
③垂直于同一条直线的两条直线垂直；
④平行于同一条直线的两条直线平行；
⑤过一点有且只有一条直线和已知直线垂直．

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图，扇形 $P O Q$ 可以绕着正六边形 $A B C D E F$ 的中心 $O$ 旋转，若 $∠ P O Q = 120 °$ ， $O P$ 等于正六边形 $A B C D E F$ 的边心距的2倍， $A B = 2$ ，则阴影部分的面积为（）

A、 $\frac{4}{3} π - 2 \sqrt{3}$ B、 $4 π - 2 \sqrt{3}$ C、 $4 π - \sqrt{3}$ D、 $\frac{16}{3} π - 4 \sqrt{3}$

查看试题解析
9. 已知正多边形的一个外角等于 $40^{\circ}$ ，那么这个正多边形的边数为 $($ $)$

A、6 B、7 C、8 D、9

查看试题解析
10. 已知关于x，y的方程组 ${\begin{array}{l} x + 3 y = 4 - a \\ x - y = 3 a \end{array}$ ，其中 $- 3 \leq a \leq 1$ ，下列命题正确的个数为（）
①当 $a = - 2$ 时，x、y的值互为相反数；

② ${\begin{array}{l} x = 5 \\ y = - 1 \end{array}$ 是方程组的解；

③当 $a = 1$ 时，方程组的解也是方程 $x + y = 4 - a$ 的解；

④若 $x \leq 1$ ，则 $1 \leq y \leq 4$ ．

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. 如图，边长为2的正方形ABCD的对称中心是坐标原点O，且 $A B ∥ x$ 轴， $A D ∥ y$ 轴，双曲线y= $\frac{1}{x}$ ， $y = - \frac{1}{x}$ 经过正方形ABCD的四个顶点，且与以2为半径的⊙O相交，则阴影部分的面积是（　　）

A、 $π$ B、 $\frac{1}{2} π$ C、 $\frac{1}{3} π$ D、 $2 π$

查看试题解析
12. 已知平行四边形 $A B C D$ 中， $∠ B = 4 ∠ A$ ，则 $∠ C$ 等于（　　）

A、 $144 °$ B、 $72 °$ C、 $54 °$ D、 $36 °$

查看试题解析

二、填空题

13. 分解因式： $x^{3} - 9 x$ =.

查看试题解析
14. $\sqrt{2} - 1$ 的相反数是， $| 3.14 - π | =$

查看试题解析
15. 若 ${(2 x - 1)}^{6} = a_{0} x^{6} + a_{1} x^{5} + a_{2} x^{4} + a_{3} x^{3} + a_{4} x^{2} + a_{5} x + a_{6}$ ，则 $a_{1} + a_{3} + a_{5}$ 的值．

查看试题解析
16. 若反比例函数 $y = \frac{m + 1}{x}$ 的图象在二、四象限，则m的取值范围为.

查看试题解析
17. 二次根式 $\sqrt{x - 3}$ 中字母x的取值范围是．

查看试题解析
18. 单项式 $- a^{2} b$ 的次数是，它与单项式 $3 a^{2} b$ 的和为．

查看试题解析

三、解答题

19. 已知：二次函数 $y = (2 m - 1) x^{2} - (5 m + 3) x + 3 m + 5$

(1)、m为何值时，此抛物线必与x轴相交于两个不同的点；

(2)、 m为何值时，这两个交点在原点的左右两边；

(3)、 m为何值时，此抛物线的对称轴是y轴；

(4)、 m为何值时，这个二次函数有最大值 $- \frac{5}{4}$ ．

查看试题解析
20. 现有四张完全相同的不透明卡片，其正面分别写有数字-2，-1，0，2，把这四张卡片背面朝上洗匀后放在桌面上.

(1)、随机抽取一张卡片，求抽取的卡片上的数字为负数的概率；

(2)、先随机抽取卡片，其上的数字作为点A的横坐标；然后放回并洗匀，再随机抽取一张卡片，其上的数字作为点A的纵坐标，试用画树状图或列表的方法求出点A在直线y=2x上的概率.

查看试题解析
21. 2022年北京冬奥会共设7个大项，15个分项和109个小项的比赛项目，北京冬奥会和残奥会的成功举办，点亮了“共创未来”的人类进步之光.某校体育组为了解全校学生对7个大项中“最喜欢观看的冬奥会比赛项目：A（滑雪），B（滑冰），C（冰球），D（冰壶），E（其他）”的情况（只选一项），随机抽取了部分学生进行调查，根据调查结果绘制出如下不完整的统计图.
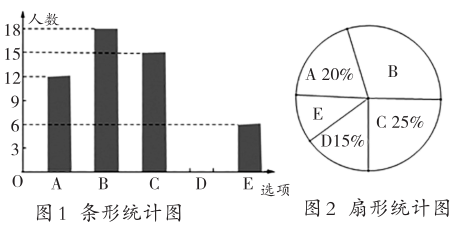
请你根据统计图回答下列问题：

(1)、请列式求本次调查共抽取多少名学生？

(2)、请补全条形统计图（图1）；

(3)、在扇形统计图中，“B（滑冰）”所对应的圆心角是多少度？

(4)、请你估计全校1200名学生中，最喜欢观看“E（其他）”项目的有多少人？

查看试题解析
22. 已知：平行四边形ABCD中，AD＝BD且∠ADB＝90°，CE平分∠BCD交AB于点E，交BD于点N，过点E作AB的垂线交AD于点F，连接BF，与线段EC交于点G．

(1)、如果边BC长为4，求△CBE的面积；

(2)、求证： $\sqrt{2}$ EG＝EN

查看试题解析
23.
如图，点D双曲线上，AD垂直x轴，垂足为A，点C在AD上，CB平行于x轴交曲线于点B，直线AB与y轴交于点F，已知AC：AD=1：3，点C的坐标为（2，2）．

(1)、求该双曲线的解析式；

(2)、求△OFA的面积．

查看试题解析
24.
如图，已知直线AB与x轴、y轴分别交于点A和点B，OA=4，且OA，OB长是关于x的方程x²﹣mx+12=0的两实根，以OB为直径的⊙M与AB交于C，连接CM，交x轴于点N，点D为OA的中点．

(1)、求证：CD是⊙M的切线；

(2)、求线段ON的长．

查看试题解析