上海市松江区2022年中考二模数学试题

试卷更新日期：2023-03-10 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中，无理数是（）

A、 $\frac{π}{2}$ B、 $\frac{22}{7}$ C、 $\sqrt{4}$ D、 $\sqrt{9}$

查看试题解析
2. 若 $a \neq 0$ ，则下列运算正确的是（）

A、 $a^{3} - a^{2} = a$ B、 $a^{3} a^{2} = a^{6}$ C、 $a^{3} + a^{2} = a^{5}$ D、 $a^{3} \div a^{2} = a$

查看试题解析
3. 下列统计量中，表示一组数据波动程度的量是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
4. 若一次函数y=kx+b的图象交y轴于正半轴，且y的值随x值的增大而减小，则（）

A、k＞0，b＞0 B、k＞0，b＜0 C、k＜0，b＞0 D、k＜0，b＜0

查看试题解析
5. 下面结论中，正确的是（）．

A、对角线相等的四边形是矩形 B、对角线互相平分的四边形是平行四边形 C、对角线互相垂直的四边形是菱形 D、对角线互相垂直且相等的四边形是正方形

查看试题解析
6. 如图，已知 $R t △ A B C$ 中， $∠ C = 90 °$ ， $t a n A = \frac{3}{4}$ ． D、E分别是边 $B C$ 、 $A B$ 上的点， $D E ∥ A C$ ，且 $B D = 2 C D$ ．如果 $⊙ E$ 经过点A，且与 $⊙ D$ 外切，那么 $⊙ D$ 与直线 $A C$ 的位置关系是（）

A、相离 B、相切 C、相交 D、不能确定

查看试题解析

二、填空题

7. 方程 $\sqrt{x + 6} = 3$ 的解是．

查看试题解析
8. 不等式组 ${\begin{array}{l} x - 1 > 1 \\ 3 x - 8 < x \end{array}$ 的解集是．

查看试题解析
9. 已知关于x的方程 $x^{2} - 2 x + k = 1$ 有两个相等的实数根，那么k的值是．

查看试题解析
10. 函数y= $\frac{1}{x - 2}$ 中，自变量x的取值范围是．

查看试题解析
11. 如果反比例函数 $y = - \frac{1}{x}$ 的图像经过 $A (2 ， a)$ 、 $B (3 ， b)$ 两点，那么a、b的大小关系是ab．（填“＞”或“＜”）．

查看试题解析
12. 如果一个正多边形的中心角为72°，那么这个正多边形的边数是．

查看试题解析
13. 甲乙两人做“石头、剪刀、布”游戏，能在一个回合中分出胜负的概率是．

查看试题解析
14. 某学校组织主题为“保护自然，爱护家园”的手抄报作品评比活动．评审组对各年级选送的作品数量进行了统计，并将统计结果绘制成两幅不完整的统计图（如图所示）．那么选送的作品中，七年级的作品份数是．

查看试题解析
15. 如图，已知梯形 $A B C D$ 中， $A B ∥ C D$ ， $A B = 2 C D$ ，设 $\vec{A B} = \vec{a}$ ， $\vec{A C} = \vec{b}$ ，那么 $\vec{A D}$ 可以用 $\vec{a}$ ， $\vec{b}$ 表示为．

查看试题解析
16. 某文具店购进一批纪念册，每本进价为20元，在销售过程中发现，该纪念册每周的销量y（本）与每本的售价x（元）之间满足一次函数关系： $y = - 2 x + 80 (20 < x < 40)$ ．已知某一周该纪念册的售价为每本30元，那么这一周的盈利是元．

查看试题解析
17. 定义：在平面直角坐标系 $x O y$ 中，O为坐标原点，对于任意两点 $P (x_{1} ， y_{1})$ 、 $Q (x_{2} ， y_{2})$ 称 $| x_{1} - x_{2} | + | y_{1} - y_{2} |$ 的值为P、Q两点的“直角距离”．直线 $y = - x + 5$ 与坐标轴交于A、B两点，Q为线段 $A B$ 上与点A、B不重合的一点，那么O、Q两点的“直角距离”是．

查看试题解析
18. 如图，在矩形 $A B C D$ 中， $A B = 2$ ， $B C = 3$ ．将矩形 $A B C D$ 绕点B顺时针旋转，得到矩形 $A^{'} B C^{'} D^{'}$ ，点A、C、D的对应点分别为 $A^{'}$ 、 $C^{'}$ 、 $D^{'}$ ．当点 $A^{'}$ 落在对角线 $A C$ 上时，点C与点 $D^{'}$ 之间的距离是．

查看试题解析

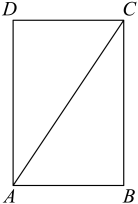
三、解答题

19. 计算： ${(- \frac{1}{2})}^{- 1} - \sqrt{18} + | 1 - \sqrt{2} | + \frac{1}{\sqrt{2} + 1}$

查看试题解析
20. 解方程组： ${\begin{array}{l} x + y = 2 \\ x^{2} - x y - 2 y^{2} = 10 \end{array}$

查看试题解析
21. 如图，已知 $⊙ O$ 是 $△ A B C$ 的外接圆， $A B = A C = 8$ ， $O A = 5$ ．

(1)、求 $∠ B A O$ 的正弦值；

(2)、求弦 $B C$ 的长．

查看试题解析
22. 小红打算买一束百合和康乃馨组合的鲜花，在“母亲节”送给妈妈．已知买2支康乃馨和3支百合共需花费28元，买3支康乃馨和2支百合共需花费27元．

(1)、求买一支康乃馨和一支百合各需多少元？

(2)、小红准备买康乃馨和百合共9支，且百合花支数不少于康乃馨支数．设买这束鲜花所需费用为w元，康乃馨有x支，求w与x之间的函数关系式，并直接写出满足上述条件且费用最少的买花方案．

查看试题解析
23. 已知：如图，两个 $△ D A B$ 和 $△ E B C$ 中， $D A = D B ， E B = E C ， ∠ A D B = ∠ B E C$ ，且点 $A 、 B 、 C$ 在一条直线上，联结 $A E 、 E D ， A E$ 与 $B D$ 交于点F．

(1)、求证： $\frac{D F}{B F} = \frac{A B}{B C}$ ；

(2)、如果 $B E^{2} = B F • B D$ ，求证： $D F = B E$ ．

查看试题解析
24. 如图，在平面直角坐标系中，已知直线 $y = 2 x + 8$ 与x轴交于点A、与y轴交于点B，抛物线 $y = - x^{2} + b x + c$ 经过点A、B．

(1)、求抛物线的表达式；

(2)、P是抛物线上一点，且位于直线 $A B$ 上方，过点P作 $P M ∥ y$ 轴、 $P N ∥ x$ 轴，分别交直线 $A B$ 于点M、N．
①当 $M N = \frac{1}{2} A B$ 时，求点P的坐标；
②连接 $O P$ 交 $A B$ 于点C，当点C是 $M N$ 的中点时，求 $\frac{P C}{O C}$ 的值．

查看试题解析
25. 已知 $△ A B C$ 中， $A B = A C$ ， $A D$ 、 $B E$ 是 $△ A B C$ 的两条高，直线 $B E$ 与直线 $A D$ 交于点Q．

(1)、如图，当 $∠ B A C$ 为锐角时，
①求证： $D B^{2} = D Q \cdot D A$ ；
②如果 $\frac{A Q}{Q D} = 3$ ，求 $∠ C$ 的正切值；

(2)、如果 $B Q = 3$ ， $E Q = 2$ ，求 $△ A B C$ 的面积．

查看试题解析