上海市普陀区2022年中考二模数学试题
试卷更新日期:2023-03-10 类型:中考模拟
一、单选题
-
1. 下列各数在数轴上所对应的点与原点的距离最远的是A、2 B、1 C、 D、2. 下列二次根式中,与是同类二次根式的是( )A、 B、 C、 D、3. 关于函数 , 下列说法中正确的是( )A、图像位于第一、三象限 B、图像与坐标轴没有交点 C、图像是一条直线 D、y的值随x的值增大而减小4. 某公司有9个子公司,某年各子公司所创年利润的情况如下表所示.
年利润(千万元)
50
4
3
1
子公司个数
1
2
2
4
根据表中的信息,下列统计量中,较为适宜表示该年各子公司所创年利润的平均水平的是( )
A、方差 B、众数 C、平均数 D、中位数5. 已知和 , 的半径长为10厘米,当两圆外切时,两圆的圆心距为25厘米,如果两圆的圆心距为15厘米时,那么此时这两圆的位置关系是( )A、内含 B、内切 C、相交 D、外离6. 如图,已知点D、E、F、G、H、I分别在的三边上,如果六边形是正六边形,下列结论中错误的是( )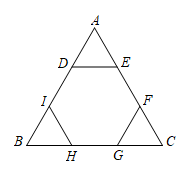 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 计算: =.8. 已知 , 那么m= .9. 方程 的根是 .10. 如果关于x的方程没有实数根,那么实数m的取值范围是 .11. 将直线沿着y轴向下平移4个单位,所得直线的表达式是 .12. 如果二次函数的图像在y轴的右侧部分是下降的,写出符合条件的一个a的值是 .13. 从-1,0,π, , 这五个数中任意抽取一个,抽取到无理数的概率是 .14. 如图,在中, , 点D在边上, , 如果°,那么度.
 15. 如图,四边形中,对角线交于点O, , , , , 如果 , 那么的值是 .
15. 如图,四边形中,对角线交于点O, , , , , 如果 , 那么的值是 . 16. 如图,已知梯形中, , , 设 , , 那么向量用向量、表示为 .
16. 如图,已知梯形中, , , 设 , , 那么向量用向量、表示为 . 17. 如图,小明和小亮进行赛跑,小亮的起跑点在小明前方10米,、 , 分别表示小亮、小明在赛跑中的路程与时间的关系.可知起跑后6秒时,小明领先小亮米.
17. 如图,小明和小亮进行赛跑,小亮的起跑点在小明前方10米,、 , 分别表示小亮、小明在赛跑中的路程与时间的关系.可知起跑后6秒时,小明领先小亮米. 18. 如图,矩形中, , . 矩形绕着点A旋转,点B、C、D的对应点分别是点、、 , 如果点恰好落在对角线上,连接 , 与交于点E,那么 .
18. 如图,矩形中, , . 矩形绕着点A旋转,点B、C、D的对应点分别是点、、 , 如果点恰好落在对角线上,连接 , 与交于点E,那么 .
三、解答题
-
19. 先化简,再求值: , 其中 .20. 解不等式组:并把解集在数轴上表示出来.
 21. 如图,在中, . 分别以点B、C为圆心、大于的同样长为半径作弧,两弧相交于点M、N,直线分别交于点D、E.
21. 如图,在中, . 分别以点B、C为圆心、大于的同样长为半径作弧,两弧相交于点M、N,直线分别交于点D、E. (1)、直线是线段的 , ;(2)、求点A到直线的距离.22. 2021年1月1日起《中华人民共和国民法典》正式施行.某社区为了解本社区的居民对该部法典的关注状况,在4000名居民中作随机抽样调查,把收集到的居民对法典的关注状况分为以下四种情况:A.十分清楚;B.清楚;C.不太清楚;D.不清楚.图1和图2是收集数据后绘制的两幅不完整统计图.
(1)、直线是线段的 , ;(2)、求点A到直线的距离.22. 2021年1月1日起《中华人民共和国民法典》正式施行.某社区为了解本社区的居民对该部法典的关注状况,在4000名居民中作随机抽样调查,把收集到的居民对法典的关注状况分为以下四种情况:A.十分清楚;B.清楚;C.不太清楚;D.不清楚.图1和图2是收集数据后绘制的两幅不完整统计图. (1)、此次接受随机抽样调查的人数是人;(2)、由样本估计总体可得,该社区居民中“十分清楚”和“清楚”的人数共有人;(3)、根据本次调查结果,为促进居民对《中华人民共和国民法典》的了解,做好普法工作,计划两年后将该社区居民中“十分清楚”和“清楚”的总人数增加到3600人,如果这两年的年增长率相同,求年增长率,23. 已知如图,四边形中, , E为对角线的中点,点F在边上,交于点G, .
(1)、此次接受随机抽样调查的人数是人;(2)、由样本估计总体可得,该社区居民中“十分清楚”和“清楚”的人数共有人;(3)、根据本次调查结果,为促进居民对《中华人民共和国民法典》的了解,做好普法工作,计划两年后将该社区居民中“十分清楚”和“清楚”的总人数增加到3600人,如果这两年的年增长率相同,求年增长率,23. 已知如图,四边形中, , E为对角线的中点,点F在边上,交于点G, . (1)、求证:四边形为菱形;(2)、如果 , 求证: .24. 如图,在平面直角坐标系中,已知抛物线与x轴交于点、 , 与y轴交于点C,顶点为D.
(1)、求证:四边形为菱形;(2)、如果 , 求证: .24. 如图,在平面直角坐标系中,已知抛物线与x轴交于点、 , 与y轴交于点C,顶点为D. (1)、求抛物线的表达式和点D的坐标;(2)、点E是第一象限内抛物线的一个动点,其横坐标为m,直线交y轴于点F.
(1)、求抛物线的表达式和点D的坐标;(2)、点E是第一象限内抛物线的一个动点,其横坐标为m,直线交y轴于点F.①用m的代数式表示直线的截距;
②在的面积与的面积相等的条件下探究:在y轴右侧存在这样一条直线,满足:以该直线上的任意一点及点C、F三点为顶点的三角形的面积都等于面积,试用规范、准确的数学语言表达符合条件的直线.
25. 如图,已知矩形中, , 以上的一点E为圆心,为半径的圆,经过点C,并交边于点F(点F不与点C重合). (1)、当时,求矩形对角线的长;(2)、设边 , 求y与x之间的函数解析式,并写出x的取值范围;(3)、设点G是的中点,且 , 求边的长.
(1)、当时,求矩形对角线的长;(2)、设边 , 求y与x之间的函数解析式,并写出x的取值范围;(3)、设点G是的中点,且 , 求边的长.